第15届蓝桥杯模拟赛第一期

news2024/11/23 8:46:27

额。。。。提前声明水文章，题目都不难。

文章目录

  • 1. 字母数
  • 2. 大乘积
  • 3. 星期几
  • 4.列名
  • 5. 最大连通
  • 6. 清理水域
  • 7. 信号覆盖
  • 8. 附近最小
  • 9. 第三小
  • 10. 3个1
  • 11. 装苹果
  • 12. 删字母
  • 13. 统计次数
  • 14. 最小数位和
  • 15. 对折次数
  • 16. 相近分解
  • 17. 电扇控制
  • 18. 最尖位置

明天就要比赛了，博主的学校没有蓝桥杯比赛项目，自己瞎学了点，自己在网上找题做，昨天在在蓝桥杯官网上看到一些刷题清单，然后刚发现的时候有点懊悔的样子，早发现的话就能跟着清单刷了，不比一个人盲目的刷好吗？
在这里插入图片描述

然后刷着刷着发现不对劲，都挺简单的，直接有自信了好吧！！！
结果刷完第一期的模拟，这题目真就是模拟呗，有点太简单了，基本上都能靠模拟做出来。
省流：8.附近最小（滑动窗口）感觉这道题可能难点。其他的真的挺简单的。
比赛前看看这些模拟题好吧，先给自己的信心满上！！！！
祝各位取得好的成绩😁😁😁。

1. 字母数

在这里插入图片描述
题目要求：
求出大于2022中第一个十六进制所有位数全部是字母的数，即每一位全部大于10；
思路：
直接从2023开始模拟就好了，发现第一个满足条件的数，那么就是答案。
答案是2730

#include <bits/stdc++.h>
using namespace std;


bool helpr(int x)
{
    while (x)
    {
       int t = x % 16;
       if (t < 10)
        return false;

        x /= 16; 
    }

    return true;
}


int main()
{
    for (int i = 2023; ; i++)
    {
        if (helpr(i))
        {
            printf("%d\n", i);
            break;
        }
    }
    return 0;
}

2. 大乘积

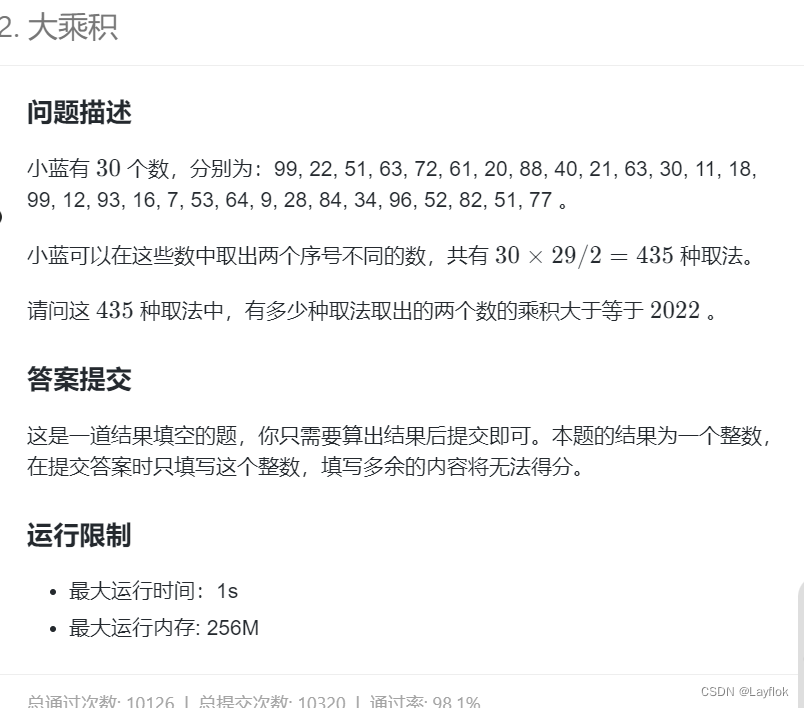
在这里插入图片描述
这道题也是填空题，直接模拟就好了。
答案是189

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int a[] = {99, 22, 51, 63, 72, 61, 20, 88, 40, 21, 63, 30, 11, 18, 99, 12, 93, 16, 7, 53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77};
    int sz = sizeof (a) / sizeof (a[0]);
    int res = 0;
    for (int i = 0; i < sz; i++)    
        for (int j = i + 1; j < sz; j++)
            if (a[i] * a[j] >= 2022)
                res++;
    printf("%d\n", res);
    return 0;   
}

3. 星期几

在这里插入图片描述
题目要求：
要求我们输入两个数w和n分别代表当前是星期几，然后经过了n天，问经过n天后是星期几。
思路：

  • 我们需要对n天除7之后剩下的余数。
  • 将余数r+原来的天数w 再除7获取余数，就是答案。
  • 如果答案是0的话，就证明原本是7.
#include <bits/stdc++.h>
using namespace std;

int w, n;

int main()
{
    scanf("%d%d", &w, &n);

    int r = n % 7;      
    int res = (w + r) % 7;
    if (res == 0)
        printf("%d\n", 7);
    else
        printf("%d\n", res);

    return 0;
}

4.列名

在这里插入图片描述
额。。。。。直接用Excel表往后拖就好了。
BYT
在这里插入图片描述

5. 最大连通

在这里插入图片描述
在这里插入图片描述
题目要求：
给一个30*60的全是由0和1构成的矩阵，然后对于1可以能来回的移动，.0则不能移动。问图中最大的连通块是多少。可以理解成1表示陆地，0表示海洋，其中最大的岛多大。
思路：
这道题是经典的图论搜索算法，可以用dfs和bfs两种方式解答。

  • 遍历所给矩阵，找到未联通的，也是未访问过的。
  • 然后对这个点进行dfs或者bfs求出所能涉及到的全部1.

dfs

void dfs(int x, int y)
{
   cur++;
   st[x][y] = true;
   for (int i = 0; i < 4; i++)
   {
       int a = x + dx[i], b = y + dy[i];
       //未越界， 能访问， 可以到。
       if (a >= 0 && a < 30 && b >= 0 && b < 60 && !st[a][b] && g[a][b] == '1')
       {
           dfs(a, b);
       } 
   }
}

bfs

void bfs(int x, int y)
{
	cur++;
	st[x][y] = true;
	queue<PII> q;
	q.push({x, y});
	
	while (q.size())
	{
		auto t = q.front();
		q.pop();
		
		for (int i = 0; i < 4; i++)
		{
			int a = t.first + dx[i], b = t.second + dy[i];
			if (a >= 0 && a < 30 && b >= 0 && b < 60 && !st[a][b] && g[a][b] == '1')
			{
				cur++;
				st[a][b] = true;
				q.push({a, b});
			}
		}
	}
}

整体代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 70;

typedef pair<int, int> PII;

char g[N][N];
bool st[N][N];
int res, cur;

int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

void dfs(int x, int y)
{
    cur++;
    st[x][y] = true;
    for (int i = 0; i < 4; i++)
    {
        int a = x + dx[i], b = y + dy[i];
        //未越界， 能访问， 可以到。
        if (a >= 0 && a < 30 && b >= 0 && b < 60 && !st[a][b] && g[a][b] == '1')
        {
            dfs(a, b);
        } 
    }
}

void bfs(int x, int y)
{
	cur++;
	st[x][y] = true;
	queue<PII> q;
	q.push({x, y});
	
	while (q.size())
	{
		auto t = q.front();
		q.pop();
		
		for (int i = 0; i < 4; i++)
		{
			int a = t.first + dx[i], b = t.second + dy[i];
			if (a >= 0 && a < 30 && b >= 0 && b < 60 && !st[a][b] && g[a][b] == '1')
			{
				cur++;
				st[a][b] = true;
				q.push({a, b});
			}
		}
	}
}


int main()
{
	for (int i = 0; i < 30; i++)
		scanf("%s", g[i]);
	
    for (int i = 0; i < 30; i++)
        for (int j = 0; j < 60; j++)
        {
            if (!st[i][j] && g[i][j] == '1')
            {
                cur = 0;
                dfs(i, j);
                //bfs(i, j);
				res = max(res, cur);
            }

        }

    printf("%d\n", res);
	return 0;
}

答案是148。

6. 清理水域

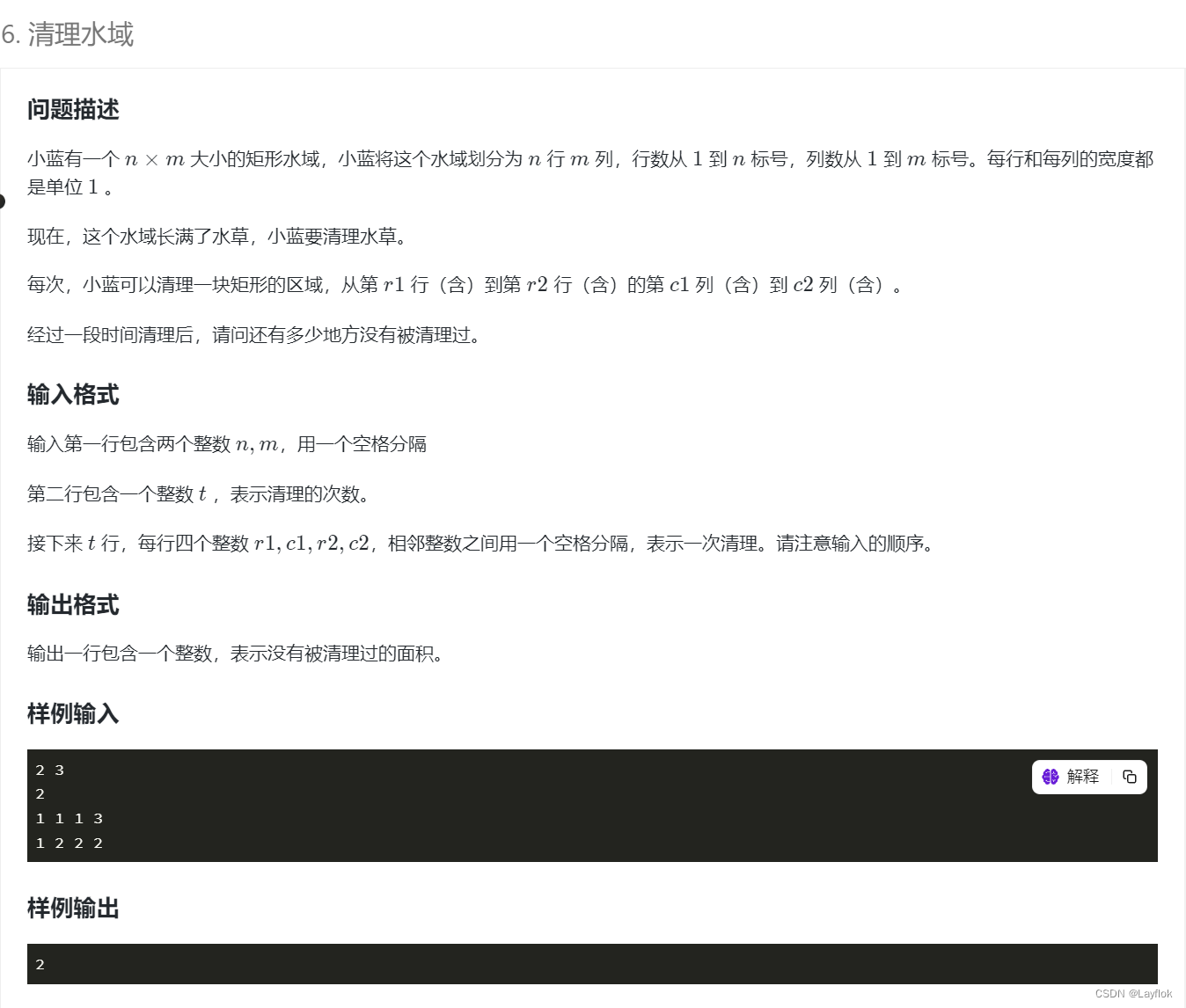
在这里插入图片描述
题目要求：
给定一个n * m的矩阵全是水草，然后对其进行清理，问说清理完成之后，还有多少没有清理。
思路：
这题暴力模拟就能过：

  • 在清理的时候，记录总共清理了多少次，重复清理不必重复计算。
  • 最后利用n * m - sum就是最后的答案。
#include <bits/stdc++.h>
using namespace std;

const int N = 110;

int n, m, k;
int g[N][N];

int main()
{
    scanf("%d%d%d", &n, &m, &k);
    int sum = 0;
    while (k --)
    {
        int r1, r2, c1, c2;
        scanf("%d%d%d%d", &r1, &c1, &r2, &c2);
        for (int i = r1; i <= r2; i++)
            for (int j = c1; j <= c2; j++)
            {
                if (g[i][j] == 0)
                    sum++;
                g[i][j] = 1;
            }
    }

    printf("%d\n", n * m - sum);
    return 0;
}

7. 信号覆盖

在这里插入图片描述
题目要求：
给一个矩阵，题目中用W和H来表示宽和高，也就是矩阵中的行和列。
然后对其进行放置n次信号塔，信号塔的坐标是r，问最后能覆盖多少个地方。
思路：
感觉和上一题的dfs很像，只是把dfs换成了检查两点之间的距离。

  • 我们遍历矩阵，然后对于每个点判断其是否被覆盖
  • 如果没有覆盖，那么去判断其是能能被覆盖。
  • 判断覆盖的check函数就是两点之间的距离公式。
#include <bits/stdc++.h>
using namespace std;

const int N = 110;

int w, h, n, r;
bool st[N][N];
int res;

bool check(int i, int j, int x, int y)
{
    return r * r >= pow(abs(i - x), 2) + pow(abs(j - y), 2);
}

int main()
{   
    scanf("%d%d%d%d", &w, &h, &n, &r);
    while (n --)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        for (int i = 0; i < w + 1; i++)
            for (int j = 0; j < h + 1; j++)
            {
                if (!st[i][j] && check(i, j, x, y))
                {
                    res++;
                    st[i][j] = true;
                }
            }
    }
    printf("%d\n", res);
    return 0;
}

8. 附近最小

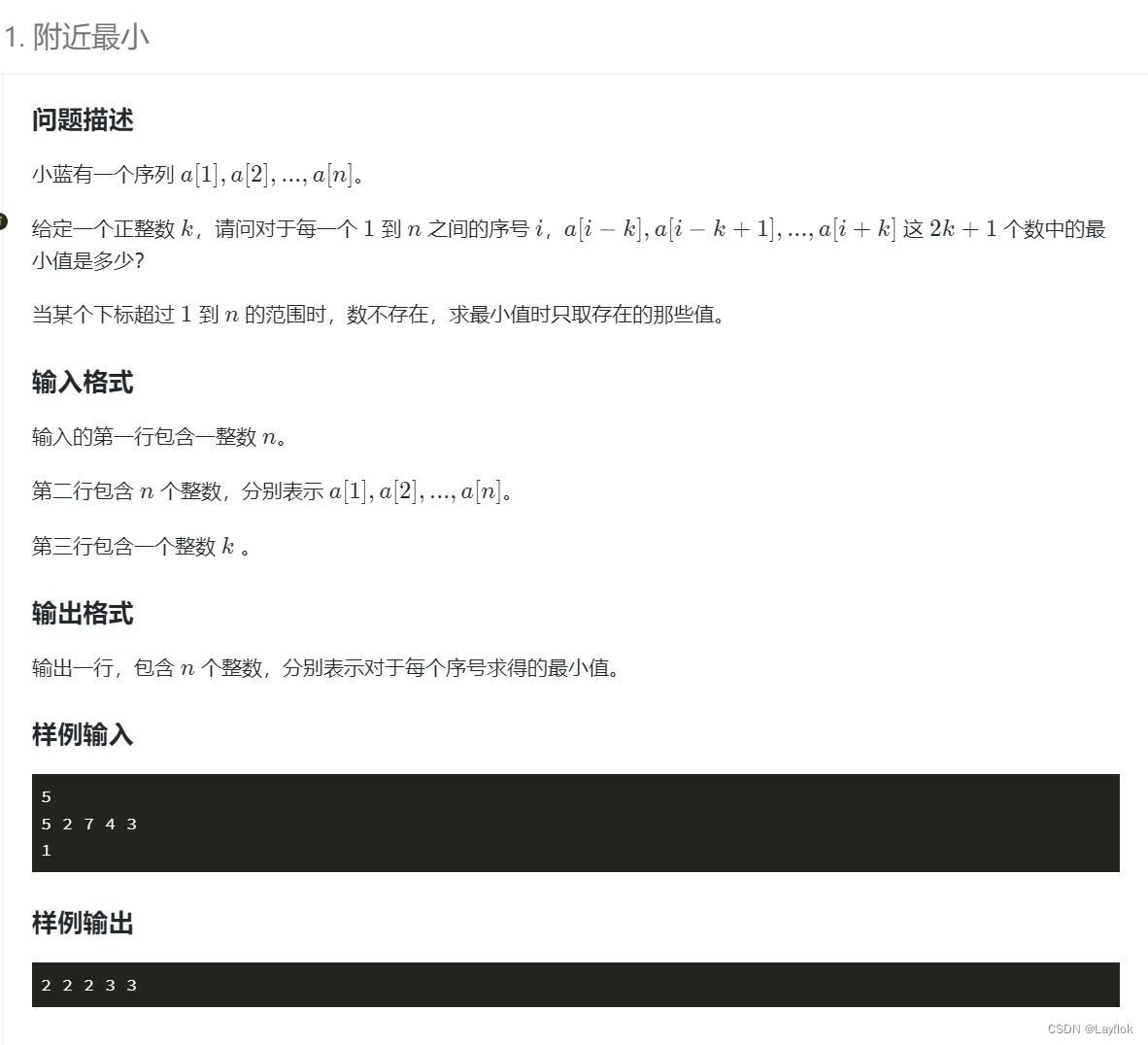
在这里插入图片描述
题目要求：
给定一个数组，然后再输入一个k来表示长度，对于每个i求出其[i - k, i + k]这段区间内的最小值。
思路：
典型的滑动窗口题目，但同样这种题目也是能够直接用暴力得到分的题目。
我们会求从[i, k]的窗口大小，那种题也算是一种模板题, 不懂得可以去Acwing去学习一下，讲的很好的。

  • 遍历数组中每一个点，然后用id表示当前这个点。
  • 构造出窗口大小l = max(i - k, 0), r = min(i + k, n - 1) 分别取边界的最值，以防止越界。
  • 然后判断对头是否不在窗口内，如果不在，将其出队列。
  • 紧接着判断当前的id是否小于等于r 并更新队尾的元素。
#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 10;

int n, k;
int a[N];
int que[N], front, rear;

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        scanf("%d", &a[i]);
    
    scanf("%d", &k);
    int id = 0;
    for (int i = 0; i < n; i++)
    {
    	//创建窗口
        int l = max(i - k, 0), r = min(i + k, n - 1);
        //判断对头是否滑出
        while (front != rear && que[front] < l) front++;
		
		//将r范围内的数入队列。
        while (id <= r)
        {
        	//对队尾进行优化
            while (front != rear && a[que[rear - 1]] >= a[id])  rear--;
            que[rear++] = id++;
        }
	
        printf("%d ", a[que[front]]);
    }
    return 0;
}

9. 第三小

在这里插入图片描述
题目要求：
给我们一个数组，然后从数组第3个位置开始，输出每一个位置上，前面第3小的数。
思路：

  • 我们定义一个优先队列（堆）出来，堆中只放3个元素，堆的建立按照大根堆来建立。
  • 此时，对于堆顶来说我们就得到第3小的数了。
  • 那对于堆的维护来说，如果说当前数组的元素比堆定元素还要小，那么此时的堆顶元素一定是会更新的，因为已经由比其更小的数进来了。

这道题目要注意，相同的数也算。
比如：9 9 8 8 3这个序列，第三小的数是8， 而不是9。

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;

int n;
int a[N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    
    priority_queue<int, vector<int>, less<int> > heap;
    for (int i = 1; i <= 3; i++)
        heap.push(a[i]);
    
    for (int i = 4; i <= n; i++)
    {
        int t = heap.top();
        printf("%d ", t);
        if (a[i] <= t)
            heap.pop(), heap.push(a[i]);
    }
    printf("%d ", heap.top());
    return 0;
}

10. 3个1

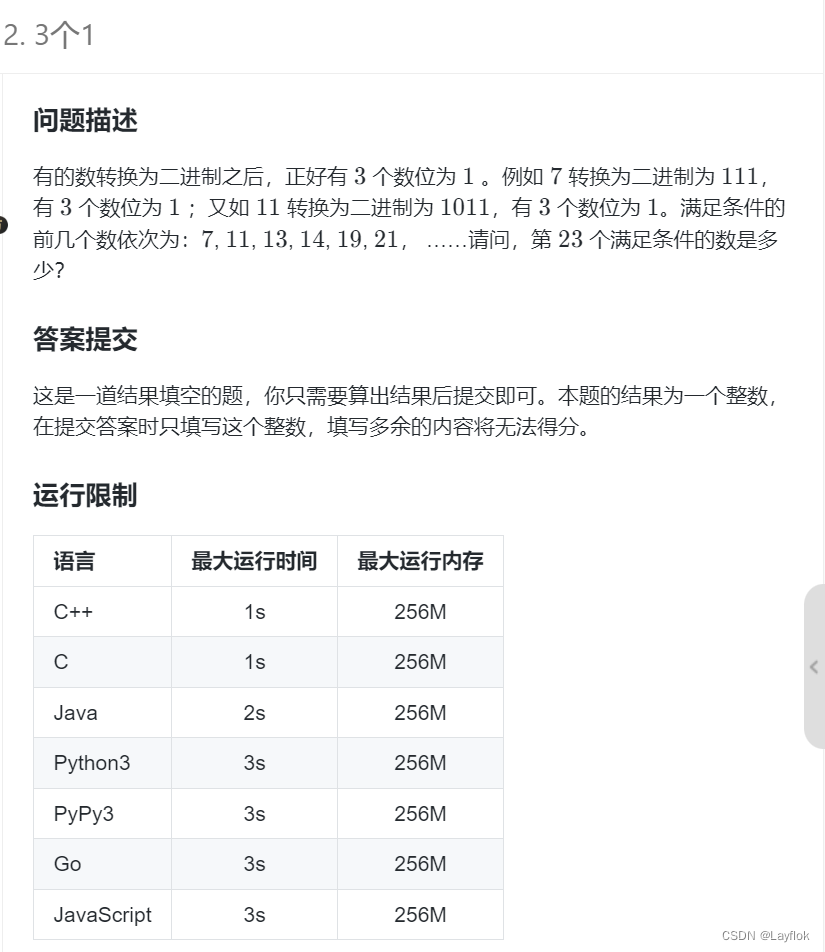
在这里插入图片描述
题目要求：
求出2进制中正好出现3个1的数，这个数是第23位。
思路：
利用lowbit(x)函数即可求出每一个数的二进制中1的位数，模板题，如果不会lowbit(x)可以取Acwing上讲过这个的模板。
答案是70

#include <bits/stdc++.h>
using namespace std;

int lowbit(int x)
{
    return x & -x;
}
int main()
{
    int res = 0;
    for (int i = 7;  ; i++)
    {
        int x = i;
        int cnt = 0;
        while (x)
        {
            x -= lowbit(x);
            cnt++;
        }
        if (cnt == 3)
            res++;

        if (res == 23)
        {
            printf("%d\n", i);
            break;
        }
    }
    return 0;
}

11. 装苹果

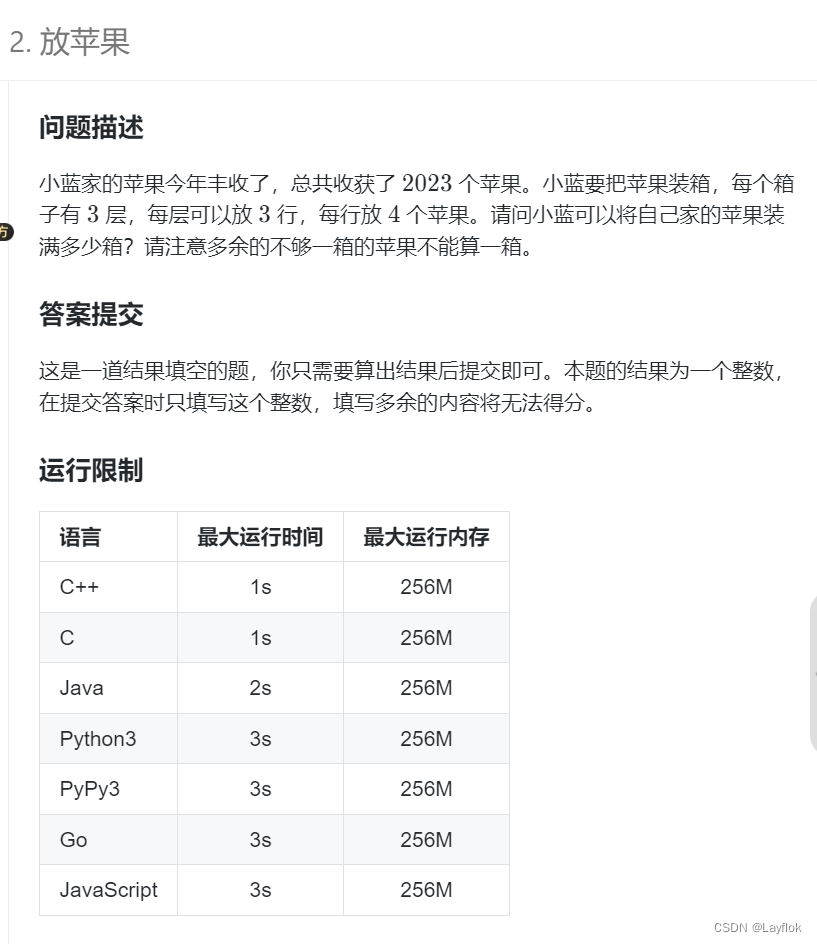
在这里插入图片描述
签到题。。。

#include <bits/stdc++.h>
using namespace std;

int main()
{
    printf("%d\n", 2023 / 36);
    return 0;
}

12. 删字母

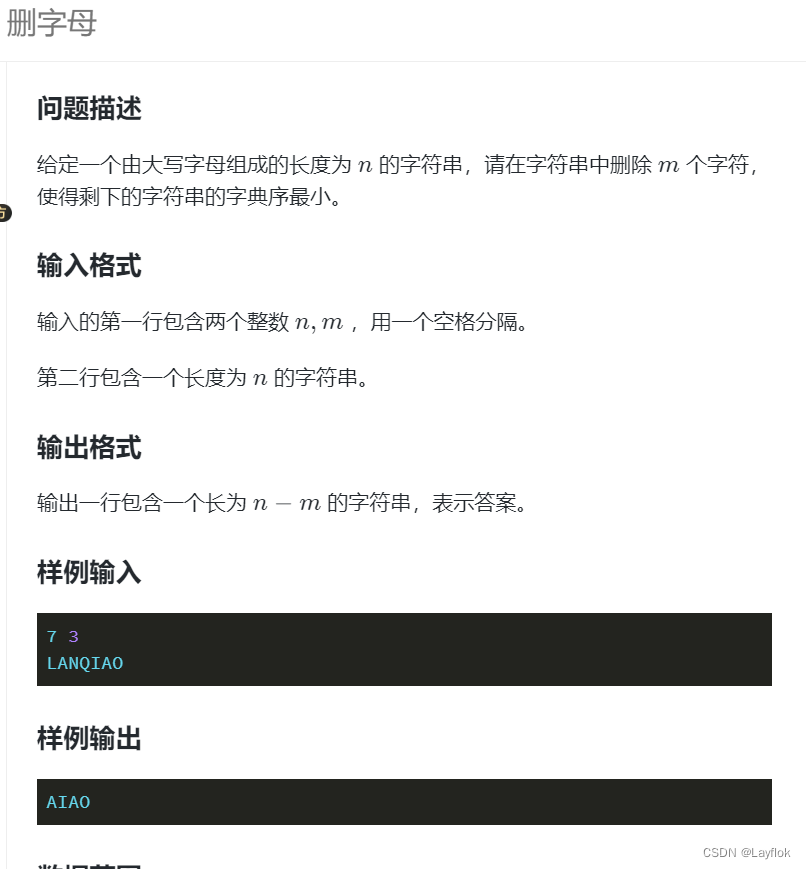
在这里插入图片描述
题目要求：
给定一个字符串，然后对其进行删除m次删除操作，使其的字典序最小。
思路：
首先这道题可以使用暴力模拟来解决，每次对字符串进行遍历，条件是：只要发现前面的一个大于后面的那一个的时候，就将其删除，这种方式删除后的字典序一定最小。
为了防止字符串原本就是升序，我们可以手动在字符串末尾加0.

#include <bits/stdc++.h>
using namespace std;

int n, m;
string s;

int main()
{
    scanf("%d%d", &n, &m);
    cin >> s;
    s.push_back('0');
    while (m--)
    {
        for (int i = 0; i < s.size() - 1; i++)
        {
            if (s[i] > s[i + 1])
            {
                s.erase(i, 1);
                break;
            }
        }
    }
    s.pop_back();
    cout << s << endl;
    return 0;
}

单调栈
这道题也可以利用单调增的栈来进行优化。

  • 去遍历字符串，如果说栈顶元素大于了当前的元素，那么对其进行出栈。
  • 如此循环，栈中就是最后的答案。
  • 注意如果说m要是不为0，需要将其栈顶的元素出栈。

但是这道题目的测试用有点弱，加上注释的代码才是正确的，但是不加也能过。
比如我下面这个两个例子：明显输出结果是错误的，却能通过整体的代码。
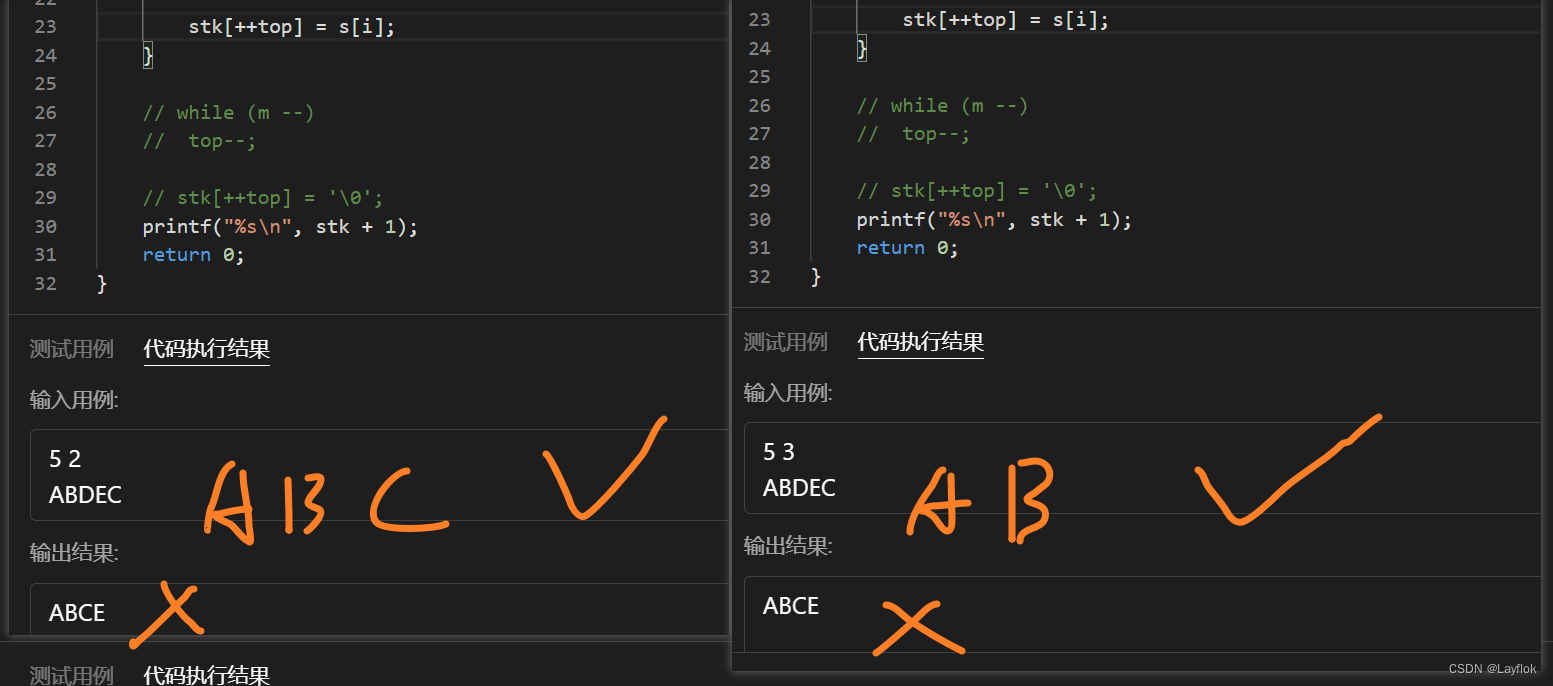
在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 10;

int n, m;
char s[N];
char stk[N];
int top;

int main()
{
    scanf("%d%d", &n, &m);
    scanf("%s", s);
    for (int i = 0; i < n; i++)
    {
        while (m && top != 0 && stk[top] > s[i])
        {
            top--;
            m--;
        }

        stk[++top] = s[i];
    }    
    
    // while (m --)
    // 	top--;
    
    // stk[++top] = '\0';
    printf("%s\n", stk + 1);
    return 0;
}

13. 统计次数

在这里插入图片描述
啊？？？？？ 昂？？？？？
题目要求：
统计字符串中1~9各个出现的次数。
思路：
哈希表。。。。

#include <bits/stdc++.h>
using namespace std;

const int N = 1e4 + 10;

int h[10];
char s[N];

int main()
{
    scanf("%s", s);

    for (int i = 0; s[i]; i++)
        h[s[i] - '0']++;

    for (int i = 0; i <= 9; i++)
        printf("%d ",h[i]);

    return 0;
}

14. 最小数位和

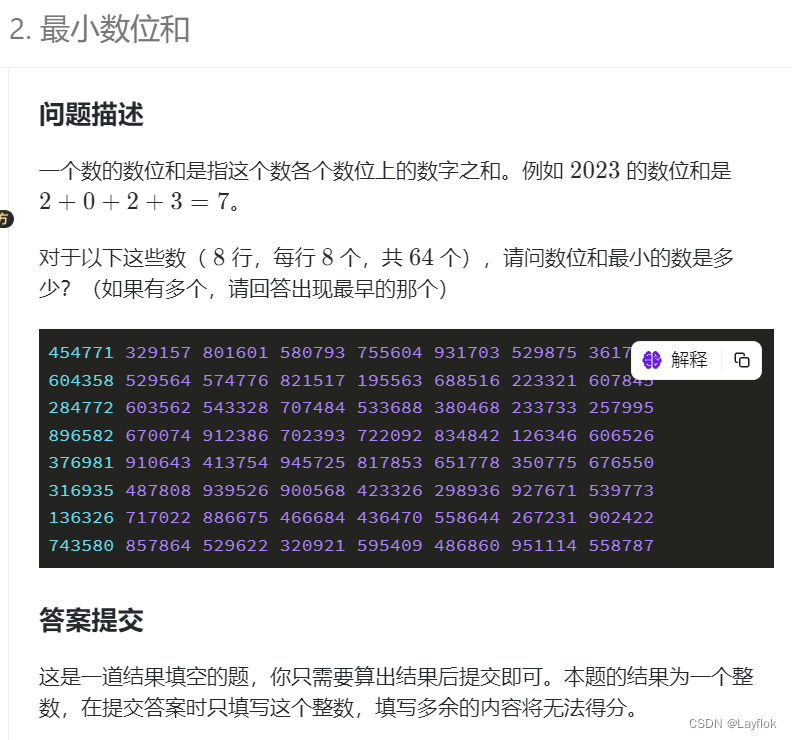
在这里插入图片描述
签到题。。只要会求一个数的每一位就好了。
答案是223321

#include <bits/stdc++.h>
using namespace std;

int a[100];

int Get_digit_Sum(int x)
{
    int sum = 0;
    while (x)
    {
        sum += x % 10;
        x /= 10;
    }

    return sum;
}


int main()
{
    for (int i = 0; i < 64; i++)
        scanf("%d", &a[i]);
    int sum = Get_digit_Sum(a[0]);
    int res = a[0];
    for (int i = 1; i < 64; i++)
    {
        int t = Get_digit_Sum(a[i]);
        if (t < sum)
        {
            sum = t;
            res = a[i];
        }
    }

    printf("%d %d\n", res, sum);
    return 0;
}

15. 对折次数

在这里插入图片描述
啊？？？？还有高手，直接模拟就好了，数据范围大，记得开long long
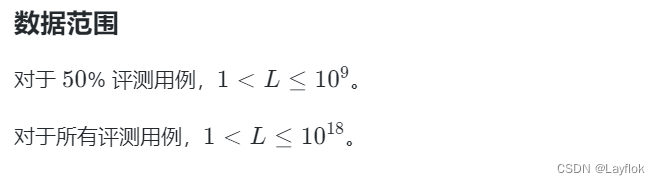
在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

int main()
{
    LL l;
    scanf("%lld", &l);
    LL cnt = 0;
    while (l)
    {
        l /= 2;
        cnt++;
    }
    printf("%lld\n", cnt);
    return 0;
}

16. 相近分解

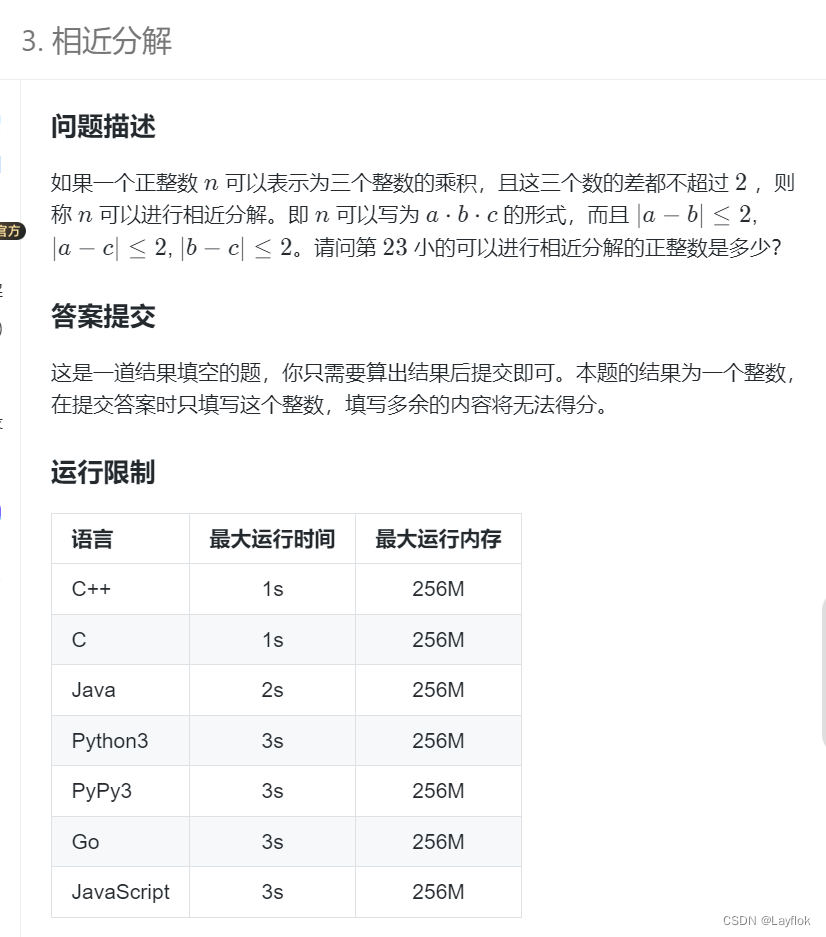
在这里插入图片描述
题目要求：
其实题目相当于说，这三个数之间的差不能超过2，然后求第23个数是多少。
思路：
我们可以直接从i = 1 开始模拟，j 和 k 的大小，不能大于 i + 2 就好了。
找到第23个就是答案.

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int cnt = 0;
    for (int i = 1; ; i++)
        for (int j = i; j <= i + 2; j++)
            for (int k = j; k <= i + 2; k++)
            {
                cnt++;
                if (cnt == 23)
                {
                    printf("%d\n", i * j * k);
                    return 0;
                }
            }

    return 0;
}

17. 电扇控制

在这里插入图片描述
嗯。。。。。找规律？？？其实也算不上。

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int p;
    scanf("%d", &p);
    if (p % 3 == 0)
        printf("low\n");
    else if (p % 3 == 1)
        printf("mid\n");
    else
        printf("high\n");
    return 0;
}
// p = 5 -- 1 2 3 4 5 
//        l m h l m h

//3 % 3 == 0 l
//4 % 3 == 1 m
//5 % 3 == 2 h

18. 最尖位置

在这里插入图片描述
差2天比赛了，做题？嗯，你做吧，一做一个不吱声，感觉自己又行了，这模拟题的难度，和真题的难度有亿点大。

#include <bits/stdc++.h>
using namespace std;

const int N = 1e4 + 10;
int n;
int a[N];

int main()
{   
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        scanf("%d", &a[i]);
    
    int res = 0;
    for (int i = 1; i < n - 1; i++)
        if (a[i] < a[i - 1] && a[i] < a[i + 1])
            res = max(res, (a[i - 1] - a[i]) * (a[i + 1] - a[i]) );
    
    printf("%d\n", res);
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1588706.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

深度学习pytorch好用网站分享

深度学习pytorch好用网站分享

深度学习在线实验室Featurizehttps://featurize.cn/而且这个网站里面还有一些学习教程 免费好用 如何使用 PyTorch 进行图像分类https://featurize.cn/notebooks/5a36fa40-490e-4664-bf98-aa5ad7b2fc2f 华为modelArtshttps://bbs.huaweicloud.com/forum/thread-76328-1-1.html…
阅读更多...
分类算法——KNN算法（二）

分类算法——KNN算法（二）

什么是K-近邻算法 1KNN原理 K Nearest Neighbor算法又叫KNN算法&#xff0c;这个算法是机器学习里面一个比较经典的算法&#xff0c;总体来说KNN算法是相对比较容易理解的算法。 定义 如果一个样本在特征空间中的k个最相似&#xff08;即特征空间中最邻近&#xff09;的样本…
阅读更多...
厂区3D全景线上漫游体验突破现实时空阻碍

厂区3D全景线上漫游体验突破现实时空阻碍

智慧园区&#xff0c;作为现代城市发展的重要引擎&#xff0c;其管理效率和安全监控的需求日益凸显。而720VR全景展示技术的引入&#xff0c;无疑为智慧园区的建设注入了新的活力。通过360全空间无死角的视觉展示&#xff0c;用户可以身临其境地感受园区的每一个角落&#xff0…
阅读更多...
VXWorks6.9 + Workbench3.3 开发环境部署

VXWorks6.9 + Workbench3.3 开发环境部署

VxWorks系列传送门 一、安装包 有需要的朋友可以私信~ 二、安装 安装挺简单 1、先安装DVD-R147826.1-1-01-vx69.udf.iso 镜像中的Setup.exe程序&#xff0c;记住要使用管理员权限 2、再安装DVD-R147826.1-23-00.iso 镜像中的Setup.exe程序&#xff0c;同样要使用管理员权限 3…
阅读更多...
数据结构--链式栈

数据结构--链式栈

一.链式栈的栈顶在哪里? 二.链栈的结构: typedef struct LSNode{ int data; struct LSNode* next; }LSNode ,*PLStack; //链栈的节点.由于栈顶在第一个数据节点,所以不需要top指针 三.链式栈的实现: //初始化LSNode* p (LSNode*)malloc(sizeof(LSNode));assert(p ! NULL)…
阅读更多...
MySQL数据库的详解（1）

MySQL数据库的详解（1）

DDL&#xff08;数据库操作&#xff09; 查询 查询所有数据库&#xff1a;show databases;当前数据库&#xff1a;select database(); 创建 创建数据库&#xff1a;create database [ if not exists] 数据库名 ; 使用 使用数据库&#xff1a;use 数据库名 ; 删除 删除数…
阅读更多...
2024年MathorCup数模竞赛C题超详细解题思路

2024年MathorCup数模竞赛C题超详细解题思路

妈妈杯本次比赛报名队伍号高达12500&#xff0c;这也就意味着大概一万只队伍参加报名&#xff0c;仅仅在报名人数这一项&#xff0c;妈妈杯已经成为美赛国赛之后的第三大竞赛。C题作为本次竞赛最简单也最容易获奖的题目&#xff0c;本文将给大家带来手把手超详细解题思路。 注…
阅读更多...
kali桥接校园网实现上网

kali桥接校园网实现上网

1.查看校园网信息 1. vim /etc/network/interfaces 添加下列信息&#xff0c;地址、网关、掩码和主机一样即可 3.vim /etc/resolv.conf 添加dns解析 4.macchanger -m AA:bb:cc:DD:ee:ff eth0(改为和主机一样的mac) 5. /etc/init.d/networking restart 重启网络即可
阅读更多...
vs2022启动cmake项目（qt+c++）

vs2022启动cmake项目（qt+c++）

1.本工程&#xff0c;如图&#xff0c;1个cmakelist.txt3个文件 2.启动vs 3.选择文件夹 4.进入这个页面&#xff0c;就说明配置没问题 5.启动 6.最后会自己生成其他文件
阅读更多...
【QT入门】 Qt自定义控件与样式设计之QPushButton实现鼠标悬浮按钮弹出对话框

【QT入门】 Qt自定义控件与样式设计之QPushButton实现鼠标悬浮按钮弹出对话框

往期回顾&#xff1a; 【QT入门】 Qt自定义控件与样式设计之qss选择器-CSDN博客 【QT入门】 Qt自定义控件与样式设计之QLineEdit的qss使用-CSDN博客 【QT入门】Qt自定义控件与样式设计之QPushButton常用qss-CSDN博客 【QT入门】 Qt自定义控件与样式设计之QPushButton实现鼠标悬…
阅读更多...
木头姐最新访谈：英伟达“卖早了”没什么，新买的Coinbase涨得更好

木头姐最新访谈：英伟达“卖早了”没什么，新买的Coinbase涨得更好

木头姐表示&#xff0c;虽然英伟达在本轮AI竞赛中处于领先地位&#xff0c;但要证明其定价合理&#xff0c;还需要找到更多能够证明AI正在加速企业收入增长的证据。她仍看好特斯拉的长期前景&#xff0c;主要基于其在自动驾驶和人形机器人领域的领先地位。 木头姐精彩观点 我们…
阅读更多...
外观模式：简化复杂系统的统一接口

外观模式：简化复杂系统的统一接口

在面向对象的软件开发中&#xff0c;外观模式是一种常用的结构型设计模式&#xff0c;旨在为复杂的系统提供一个简化的接口。通过创建一个统一的高级接口&#xff0c;这个模式帮助客户端通过一个简单的方式与复杂的子系统交互。本文将详细介绍外观模式的定义、实现、应用场景以…
阅读更多...
Java 怎么捕捉 Windows 中前台窗口的改变？

Java 怎么捕捉 Windows 中前台窗口的改变？

在Java中捕捉Windows中前台窗口的改变通常需要使用JNI&#xff08;Java Native Interface&#xff09;来调用Windows API。Windows API提供了一系列函数来获取有关窗口和进程的信息&#xff0c;通过使用这些函数&#xff0c;我们可以实现在Java程序中监视和捕捉Windows前台窗口…
阅读更多...
redux-persist

redux-persist

npm install redux-persist 目录&#xff1a;&#xff08;分模块&#xff09; 之前未加入持久化的代码&#xff1a; import { legacy_createStore as createStore } from redux import { combineReducers } from "redux"; import countReducer from ./modules/cou…
阅读更多...
小红的白色字符串

小红的白色字符串

题目描述 小红拿到了一个字符串&#xff0c;她准备将一些字母变成白色&#xff0c;变成白色的字母看上去就和空格一样&#xff0c;这样字符串就变成了一些单词。 现在小红希望&#xff0c;每个单词都满足以下两种情况中的一种&#xff1a; 1.开头第一个大写&#xff0c;其余为…
阅读更多...
基于linux进一步理解核间通讯

基于linux进一步理解核间通讯

芯片架构分为同构和异构： 如下图TC397： 如下图TDA4： 如下图STM32MP157： 非对称多处理结构(AMP)： AMP 结构是指每个内核运行自己的 OS 或同一 OS 的独立实例&#
阅读更多...
bugku-web-file_get_contents

bugku-web-file_get_contents

<?php extract($_GET); if (!empty($ac)){$f trim(file_get_contents($fn));if ($ac $f){echo "<p>This is flag:" ." $flag</p>";}else{echo "<p>sorry!</p>";} } ?> 这里涉及到几个不常用的函数 这里直接构…
阅读更多...
UE 模型学习

UE 模型学习

1. UE中任何模型都是有多个三角面构成的&#xff0c;模型有一个顶点数组&#xff0c;根据右手螺旋定则和三个顶点顺序确定三角面的法线。 注&#xff1a;当三角面的法线方向与相机法线方向相同时&#xff0c;此时看不见三角面&#xff1b;当两法线方向相反&#xff0c;此时才能…
阅读更多...
企业搭建分销商城系统要注意什么？

企业搭建分销商城系统要注意什么？

分销商城系统是一种专门设计出来的电商平台&#xff0c;旨在通过构建多层级的分销网络体系&#xff0c;帮助企业将产品或服务高效地推广和销售至终端消费者。那么&#xff0c;搭建分销商城系统要注意什么呢&#xff1f;我们从优势、功能、玩法来进行分析。 一、分销商城有哪些…
阅读更多...
Faster RCNN训练自己的数据集【傻瓜式教程】

Faster RCNN训练自己的数据集【傻瓜式教程】

一、下载源码 本文采用的源码是&#xff1a;https://github.com/dBeker/Faster-RCNN-TensorFlow-Python3 二、配置环境 由于本文是小白教程&#xff0c;光写几个环境怕有人配置不好或者配置版本搞乱。Faster RCNN配置环境比较复杂。我在这直接贴图我的环境版本图&#xff1a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023