动态规划在矩阵链乘法中的应用：寻找最优括号化方案

news2024/11/24 8:30:18

动态规划在矩阵链乘法中的应用：寻找最优括号化方案

一、问题描述
二、动态规划的基本概念
三、矩阵链乘法问题的动态规划解法
四、伪代码
五、C语言代码示例
六、计算括号化方案的数量
七、结论

计算括号化方案的数量问题是计算机科学中的一个经典问题，它涉及到动态规划这一重要的算法设计技术。在本文中，我们将详细介绍如何使用动态规划来解决矩阵链乘法问题，以及如何计算括号化方案的数量。我们将从问题的描述开始，逐步深入到动态规划的核心概念，并通过伪代码和C语言代码示例来具体展示解决方案。
在这里插入图片描述

一、问题描述

给定一系列矩阵，我们需要计算这些矩阵的乘积。矩阵乘法满足结合律，这意味着我们可以以不同的方式添加括号来改变计算的顺序。不同的括号化方案会导致不同的计算成本，因为不同大小的矩阵相乘所需的标量乘法次数不同。我们的目标是找到一种最优的括号化方案，使得计算矩阵乘积的总成本最低。

二、动态规划的基本概念

动态规划是一种解决复杂问题的方法，它将问题分解为更小的子问题，并将子问题的解存储起来，以便在后续需要时可以重复使用，从而避免重复计算。动态规划的关键特点是最优子结构和子问题重叠。

最优子结构：一个问题的最优解包含其子问题的最优解。
子问题重叠：不同的子问题可能包含相同的更小子问题。

三、矩阵链乘法问题的动态规划解法

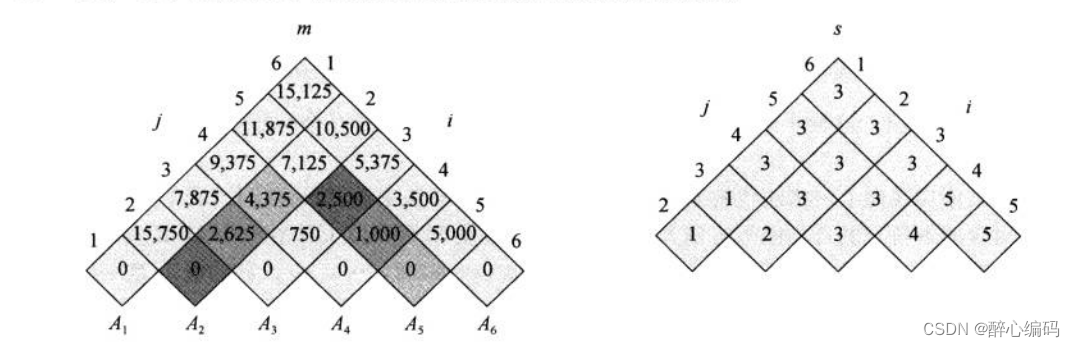
对于矩阵链乘法问题，我们可以使用动态规划来找到最优的括号化方案。我们定义一个二维数组m[i, j]来存储计算矩阵链A[i]A[i+1]...A[j]的最小代价。这里，p[i]表示矩阵A[i]的行数和列数。

我们的目标是计算m[1, n]，其中n是矩阵链的长度。我们可以通过以下递归关系来计算m[i, j]：

m[i, j] = min{m[i, k] + m[k+1, j] + p[i-1]*p[k]*p[j]}

其中，k是介于i和j之间的任意整数。

四、伪代码

function MATRIX_CHAIN_ORDER(p):
    n = length(p) - 1
    m = create 2D array of size (1 to n, 1 to n)
    s = create 2D array of size (1 to n-1, 2 to n)

    for i from 1 to n:
        m[i, i] = 0

    for l from 2 to n: // l is the chain length
        for i from 1 to n - l + 1:
            j = i + l - 1
            m[i, j] = infinity

            for k from i to j - 1:
                q = m[i, k] + m[k+1, j] + p[i-1]*p[k]*p[j]
                if q < m[i, j]:
                    m[i, j] = q
                    s[i, j] = k

    return m, s

五、C语言代码示例

#include <stdio.h>
#include <stdlib.h>

int **create2DArray(int rows, int cols) {
    int **array = (int **)malloc(rows * sizeof(int *));
    for (int i = 0; i < rows; i++) {
        array[i] = (int *)malloc(cols * sizeof(int));
    }
    return array;
}

void free2DArray(int **array, int rows) {
    for (int i = 0; i < rows; i++) {
        free(array[i]);
    }
    free(array);
}

void matrixChainOrder(int *p, int n) {
    int **m = create2DArray(n, n);
    int **s = create2DArray(n-1, n);

    for (int i = 0; i < n; i++) {
        m[i][i] = 0;
    }

    for (int l = 2; l <= n; l++) { // l is the chain length
        for (int i = 0; i < n - l + 1; i++) {
            int j = i + l - 1;
            m[i][j] = (int)1e9;

            for (int k = i; k < j; k++) {
                int q = m[i][k] + m[k+1][j] + p[i] * p[k+1] * p[j+1];
                if (q < m[i][j]) {
                    m[i][j] = q;
                    s[i][j] = k;
                }
            }
        }
    }

    // Print the results
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            printf("m[%d][%d] = %d\n", i, j, m[i][j]);
        }
    }

    free2DArray(m, n);
    free2DArray(s, n-1);
}

int main() {
    int p[] = {30, 35, 15, 5, 10, 20, 25};
    int n = sizeof(p) / sizeof(p[0]) - 1;
    matrixChainOrder(p, n);
    return 0;
}