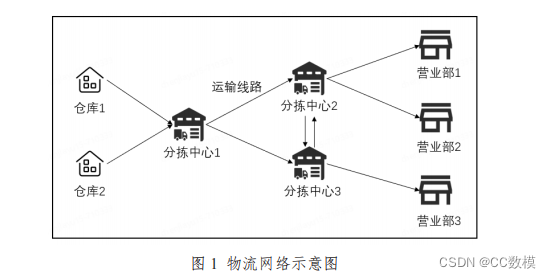
电商物流网络在订单履约中由多个环节组成,图1是一个简化的物流网络示意图。其中,分拣中心作为网络的中间环节,需要将包裹按照不同流向进行分拣并发往下一个场地,最终使包赛到达消费者手中。分拣中心管理效率的提升,对整体网络的履约效率和运作成本起着十分重要的作用,分拣中心的货量预测是电商物流网络重要的研究问题,对分拣中心货量的精准预测是后续管理及决策的基础,如果管理者可以提前预知之后一段时间各个分拣中心需要操作的货量,便可以提前对资源进行安排。在此场景下的货量预测目标一般有两个:一是根据历史货量、物流网络配置等信息,预测每个分拣中心每天的货量;二是根据历史货量小时数据,预测每个分拣中心每小时的货量。 分拣中心的货量预测与网络的运输线路有关,通过分析各线路的运输货量,可以得出各分拣中心之间的网络连接关系。当线路关系调整时,可以参考线路的调整信息,得到各分拣中心货量更为准确的预测。 基于分拣中心货量预测的人员排班是接下来要解决的重要问题,分拣中心的人员包含正式工和临时工两种:正式工是场地长期雇佣的人员,工作效率较高:临时工是根据货量情况临时招募的人员,每天可以任意增减,但工作效率相对较低、雇佣成本较高。根据货量预测结果合理安排人员,旨在完成工作的情况下尽可能降低人员成本。针对当前物流网络,其人员安排班次及小时人效指标情况如下: 1)对于所有分拣中心,每天分为6个班次,分别为:00:00-08:00,05:00-13:00,08:00-16:00,12:00-20:00,14:00-22:00,16:00-24:00,每个人员(正式工或临时工)每天只能出勤一个班次;2)小时人效指标为每人每小时完成分拣的包裹量(包裹量即货量),正式工的最高小时人效为 25 包裹/小时,临时工的最高小时人效为 20包裹/小时。 该物流网络包括57个分拣中心,每个分拣中心过去4个月的每天货量如附件1所示,过去 30天的每小时货量如附件2所示。
问题 1:建立货量预测模型,对57 个分拣中心未来 30 天每天及每小时的货量进行预测,将预测结果写入结果表1和表2中。
为了建立一个货量预测模型,我们将使用季节性时间序列模型来预测每个分拣中心未来30天的每天及每小时的货量。在这里,我们将使用季节性ARIMA(SARIMA)模型,它是非常适合处理具有季节性模式的时间序列数据的。
1. 数据探索和预处理
假设我们的时间序列是 yt,其中 t 表示时间点。
数据清洗:
检查缺失值:如果在 yt 中存在缺失值,我们需要决定是填补这些缺失值还是删除相关的时间点。
异常值处理:识别并处理任何异常值,例如,通过箱型图识别的离群点。
2. 季节性时间序列建模:SARIMA模型
SARIMA模型的全称是季节性自回归积分滑动平均模型,表示为 SARIMA(,,P,D,Q)s,其中:
p:非季节性自回归项的阶数。
d:非季节性差分次数。
q:非季节性移动平均项的阶数。
P:季节性自回归项的阶数。
D:季节性差分次数。
Q:季节性移动平均项的阶数。
s:时间序列的季节长度。
SARIMA模型的数学表示:
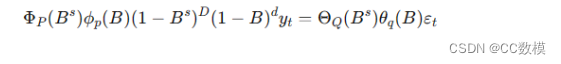
3. 参数估计
在SARIMA模型的参数估计中,最常用的方法是最大似然估计(MLE)。假设我们的时间序列数据为 y1,y2,…,yn,模型参数集合为 θ=(p,d,q,P,D,Q,s) 和其他相关参数,如自回归和移动平均参数。最大似然估计旨在找到参数集合 θ 的值,使得观察到的数据出现的可能性(似然函数)最大。
似然函数 L 通常表示为:

其中 (∣)f(y∣θ) 是给定参数 θ 下观察数据 y 的概率密度函数。
最大化似然函数等价于最大化其对数形式,即最大化对数似然函数 ℓ()ℓ(θ):
![]()
参数估计的目标是:
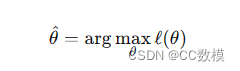
4. 模型检验
赤池信息准则(AIC)
AIC是一种衡量统计模型拟合优度的准则,它旨在选择最佳模型,并对模型复杂度进行惩罚。AIC的计算公式为:

其中,k 是模型参数的数量,L 是最大似然函数的值。
贝叶斯信息准则(BIC)
BIC与AIC相似,但对模型中参数的数量给予更大的惩罚。BIC的计算公式为:
![]()
其中,n 是样本大小,k 和 L 的定义同上。
残差诊断
对于残差 εt,我们希望它们是白噪声序列。这可以通过残差的自相关函数(ACF)和偏自相关函数(PACF)图来检查,或者使用Ljung-Box Q检验来统计检验残差序列中的自相关性是否显著不同于零。
Ljung-Box Q检验的假设检验公式为:

其中,n 是样本大小,^ρk 是残差序列的自相关系数,m 是滞后期数。检验的目的是确定序列中是否存在显著的自相关性。
通过上述步骤,您可以对模型进行充分的参数估计和模型检验,以确保预测的准确性和可靠性。
源代码以及结果如下,完整见附件!


问题2:过去 90天各分拣中心之间的各运输线路平均货量如附件3所示。若未来30 天分拣中心之间的运输线路发生了变化,具体如附件4所示。根据附件 1-4,请对 57个分拣中心未来30天每天及每小时的货量进行预测,并将预测结果写入结果表3和表4中。
问题2要求基于现有和未来的运输线路变化来预测各分拣中心未来30天的每天及每小时货量。这个问题的建模过程需要考虑分拣中心间的运输线路变化对货量的影响。具体的数学建模过程和公式如下:
数据预处理
加载数据:加载四个附件的数据,理解其结构和内容。
数据合并:将过去的货量数据(附件1和附件2)、当前运输线路的平均货量数据(附件3)和未来运输线路变化(附件4)整合,以便分析。
建模过程
基础货量预测:首先,像问题1一样,对每个分拣中心进行货量预测,忽略运输线路的影响,得到基础预测值。
线路影响分析:分析附件3中的运输线路平均货量数据,计算每条线路对应分拣中心的平均影响值。
未来线路调整:根据附件4的未来线路变化,计算每个分拣中心因线路变化而增减的货量。
综合预测修正:将步骤1的基础预测值与步骤3的调整值相结合,得到最终的货量预测。
假设 ,Yc,t 表示分拣中心 c 在时间 t 的货量预测,,,Lc,l,t 表示分拣中心 c 在时间 t 通过线路 l 的平均货量,Ac,l,t 表示线路调整后分拣中心 c 在时间 t 通过线路 l 的额外货量。


问题3:假设每个分拣中心有60名正式工,在人员安排时将优先使用正式工,若需额外人员将使用临时工。请基于问题2的预测结果建立模型,给出未来 30 天每个分拣中心每个班次的出勤人数,并写入结果表5中。要求在每天的货量处理完成的基础上,安排的人天数(例如30天每天出勤200名员工,则总人天数为6000)尽可能少,且每天的实际小时人效尽量均衡。

问题4:研究特定分拣中心的排班问题,这里不妨以SC60为例,假设分拣中心 SC60 当前有 200名正式工,请基于问题2的预测结果建立模型确定未来 30 天每名正式工及临时工的班次出勤计划,即给出未来 30 天每天六个班次中,每名正式工将在哪些班次出勤,每个班次需要雇佣多少临时工,并写入结果表6中。每名正式工的出勤率(出勤的天数除以总天数30)不能高于85%,且连续出勤天数不能超过7天。要求在每天货量处理完成的基础上,安排的人天数尽可能少,每天的实际小时人效尽量均衡,且正式工出勤率尽量均衡。
完整内容见附件!
附件: