在本文中,我们将学习如何在Python中进行指数和对数曲线拟合。首先我们要问的问题是什么是曲线拟合?
曲线拟合是构造曲线或数学函数的过程,其具有对一系列数据点的最佳拟合,可能受到约束。
- 对数曲线拟合:对数曲线是对数函数的曲线图。
- 指数曲线拟合:指数曲线是指数函数的曲线图。
让我们考虑两个方程
y = alog(x) + b 其中a、b是该对数方程的系数。
y = e(ax)*e(b)
我们将在上面的方程上拟合两条曲线,并找到最佳拟合曲线。对于Python中的曲线拟合,我们将使用一些库函数。
我们还将使用numpy.polyfit()方法来拟合曲线。这个函数有三个参数x,y,多项式次数(n)返回n次多项式的系数。
语法:numpy.polyfit(x,y,deg)
主要参数:
x-> x坐标
y-> y坐标
deg ->拟合多项式的阶数。因此,如果给定deg为1,我们得到线性多项式的系数,或者如果它为2,我们得到二次多项式的系数。
对数曲线拟合
import numpy as np
# It is for plotting the curve
import matplotlib.pyplot as plt
由于我们已经导入了所需的库,因此必须创建两个名为x和y的数组。在创建这两个数组之后,我们必须在numpy.log()方法的帮助下获取x和y中的值的对数。
# Points on X-axis
x_data = np.array([11, 23, 31, 43, 51])
# Points on Y-axis
y_data = np.array([2, 4, 6, 8, 10])
print(x_data)
print(y_data)
# Taking log of x values
xlog_data = np.log(x_data)
print(xlog_data)
输出

之后,得到x和y数组的对数值,在numpy.polyfit()的帮助下,我们找到了方程的系数。由于我们采用了线性方程,因此在polyfit方法中,我们将在度参数中传递1。
# Given log values of x , y as input
curve = np.polyfit(log_x_data, y_data, 1)
print(curve)
输出

所以我们得到系数为[5.04,-10.79],我们可以得到曲线的方程为(y= a*log(x)+y,其中a,b是系数)
y = 5.04 * log_x_data - 10.79
print(y)
输出

现在,让我们用xlog_data,ylog_data绘制一个图,另一个用xlog_data和我们得到的y方程绘制一个图。为了在python中绘制图形,我们将使用Matplotlib.pyplot.plot()函数。
# Blue color
plt.plot(log_x_data, y_data)
# Best fit in orange
plt.plot(log_x_data, y)

在上图中,黄线表示原始x和y坐标的图,蓝线是我们通过计算获得的坐标图,它是最佳拟合。
指数曲线拟合
我们将重复上述相同的过程,但唯一的区别是对数函数被指数函数取代。
x_data = np.array([11, 19, 31, 39, 51])
print(x_data)
y_data = np.array([5, 8, 32, 84, 110])
print(y_data)

ylog_data = np.log(y_data)
print(ylog_data)
curve_fit = np.polyfit(x_data, log_y_data, 1)
print(curve_fit)

所以,a = 0.69和b = 0.085,这些是系数,我们可以得到曲线的方程,即(y = e(ax)*e(b),其中a,b是系数)
y = np.exp(0.69) * np.exp(0.085*x_data)
print(y)
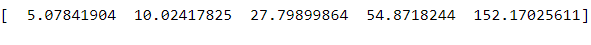
现在,让我们在Matplotlib.pyplot.plot()函数的帮助下绘制图表。
# Blue
plt.plot(x_data, y_data)
# best fit in orange
plt.plot(x_data, y)

在上图中,蓝线表示原始x和y坐标的图形,黄线是我们通过计算获得的坐标图形,它是最佳拟合。