写这篇blog是因为多方参考才读懂这两篇文章,希望能用自己的语言表达出来加深一下理解。因为是刚刚开始学习这部分内容,错误之处敬请指出。
文章目录
- 前言
- 算子Operator概念理解
- 问题建立
- Graph Neural Operator的思想
- 证明
- 采样多少个数据点可以用来表示一组a_j和u_j?
- Fourier Neural Operator的思想
- 直观对比CNN滤波和Fourier滤波
前言
2022年Nvidia发表在arXiv上的的FourcastNet作为几乎是最早的一篇气象大模型的工作(之前Google Research的MetNet主要还是对于降水的预报)。除了Transformer的backbone之外,使用到了2021年发表在ICLR上的Fourier Neural Operator。为了更好的理解模型的理论基础,可以详细学习一下 Fourier neural operator for parametric partial differential equations 以及他的前期工作 Neural operator: graph kernel network for PDE。
文章指路:
GNO
FNO
作者对这两篇文章的解析blog
算子Operator概念理解
算子(Operator)是函数空间到函数空间的映射。从广义上讲,对任何函数进行某一项操作都可以看作是一个算子。在神经网络中例如convolution,fully connected layer等,都可以当作一种算子。
因此,区别于之前的一些PINN文章,从 给定的一个函数中采样 x x x和对应的 y y y,建立一个神经网络来学习这个函数,本篇文章中提到的Operator旨在学习一个函数簇到另一个函数簇的映射。例如,具有不同初始条件的Burgers方程,到这些方程的解的映射,是这个神经网络算子需要学习的内容。
因此他的好处在于,对于某种表达形式的方程,例如Burgers方程,训练一个算子可以得到Burgers方程不同初始条件下的解。而文章中所提到的参数 a a a,可以理解成初始条件/边界条件/含有物理意义的系数等。
问题建立

假设我们有一个一般的二阶椭圆偏微分方程,其中u是需要求解的函数,f(x)是右端项,a(x)是参数。一般的,f(x)和a(x)均为已知。f(x)也可以理解成物理方程中的强迫项。方程可以以算子的形式表示,如下图所示。
偏微分方程一般可以写成上述形式。
L
a
L_a
La表示在参数
a
a
a是的算子。

作者希望用神经网络来模拟映射关系F,实现一组方程在给定不同参数a的情况下,求得方程的解。其中,A是参数a的集合,或者理解成参数空间。
在这种情况下,神经网络的输入和输出都是函数的表达式。为了能表示出函数,作者在
a
a
a和
u
u
u上进行了K个点的采样
P
i
=
1
,
…
,
K
P_{i=1,…,K}
Pi=1,…,K,并通过
a
j
∣
P
k
a_j | P_k
aj∣Pk 和
u
j
∣
P
k
u_j | P_k
uj∣Pk作为网络的输入输出来进行训练。
Graph Neural Operator的思想
作者考虑使用格林函数(Green Function)作为PDE的求解方法。格林函数是一种用来解有初值条件和边界条件的非齐次微分方程的函数。
证明
若可找到线性算符L的格林函数G,则有 由于
L
a
u
(
x
)
=
f
(
x
)
L_au(x) = f(x)
Lau(x)=f(x),则可以得到
L
a
u
(
x
)
=
∫
L
G
(
x
,
s
)
f
(
s
)
d
s
L_au(x) = \int LG(x,s)f(s)ds
Lau(x)=∫LG(x,s)f(s)ds。其中,L算子只对x起作用,不对被积分的变量s起作用,因此可以得到
L
a
u
(
x
)
=
L
∫
G
(
x
,
s
)
f
(
s
)
d
s
L_au(x)= L\int G(x,s)f(s)ds
Lau(x)=L∫G(x,s)f(s)ds,所以也可以得到
u
(
x
)
=
∫
G
(
x
,
s
)
f
(
s
)
d
s
u(x) = \int G(x,s)f(s)ds
u(x)=∫G(x,s)f(s)ds,其中s表示定义域中的某一个点,例如G(1,0)就表示x=0对x=1这个点的影响。因此对
s
s
s进行积分,就可以理解成要求解定义域中的点对x的影响。
由于
L
a
u
(
x
)
=
f
(
x
)
L_au(x) = f(x)
Lau(x)=f(x),则可以得到
L
a
u
(
x
)
=
∫
L
G
(
x
,
s
)
f
(
s
)
d
s
L_au(x) = \int LG(x,s)f(s)ds
Lau(x)=∫LG(x,s)f(s)ds。其中,L算子只对x起作用,不对被积分的变量s起作用,因此可以得到
L
a
u
(
x
)
=
L
∫
G
(
x
,
s
)
f
(
s
)
d
s
L_au(x)= L\int G(x,s)f(s)ds
Lau(x)=L∫G(x,s)f(s)ds,所以也可以得到
u
(
x
)
=
∫
G
(
x
,
s
)
f
(
s
)
d
s
u(x) = \int G(x,s)f(s)ds
u(x)=∫G(x,s)f(s)ds,其中s表示定义域中的某一个点,例如G(1,0)就表示x=0对x=1这个点的影响。因此对
s
s
s进行积分,就可以理解成要求解定义域中的点对x的影响。
如果进行离散采样,并且把所有离散点看作图神经网络中的节点的话,点对x的影响可以看作是图神经网络的边的传递。
采样多少个数据点可以用来表示一组a_j和u_j?
即上述K为多少比较合适?
考虑有向边,建立图神经网络的复杂度为O(k^2)。根据Monte Carlo integration 的error【这边暂时还没理解为什么看这个error,可能理解错了】,error和采样点的关系为 δ ∼ K − 1 / 2 \delta \sim K^{-1/2} δ∼K−1/2。当对函数采样200个点时(对于每一组函数对,训练用400个,测试用200个),就已经可以达到比较好的效果。
Fourier Neural Operator的思想
如果将图神经网络中的message passing替换成Fourier变换和逆变换层,则可以得到FNO的大致结构,如下图所示。FNO是图片— 图片的学习。

具体的,对于每一层神经网络的输入,FNO层做三件事情:
- 对于输入进行傅立叶变换
- 过滤掉比较高频的modes,这一步我自己的理解是为了消除一些采样的噪声等,提高模型的鲁棒性
- 对于低频modes进行傅立叶逆变换。
W为bias term,用shortcut的方式增加一个偏差项(线性)。因为傅立叶具有周期性,通过激活函数 σ \sigma σ来恢复函数的非周期边界条件和一些高频modes。
直观对比CNN滤波和Fourier滤波
作者在blog中给出了很直观的Fourier filter和CNN filter的比对。CNN的filter可以很好的捕捉局部的特征,可以很好的提出图片的边缘信息。而傅立叶filter是 全局 的,并且是三角函数,因此可以更好的用来表示连续方程。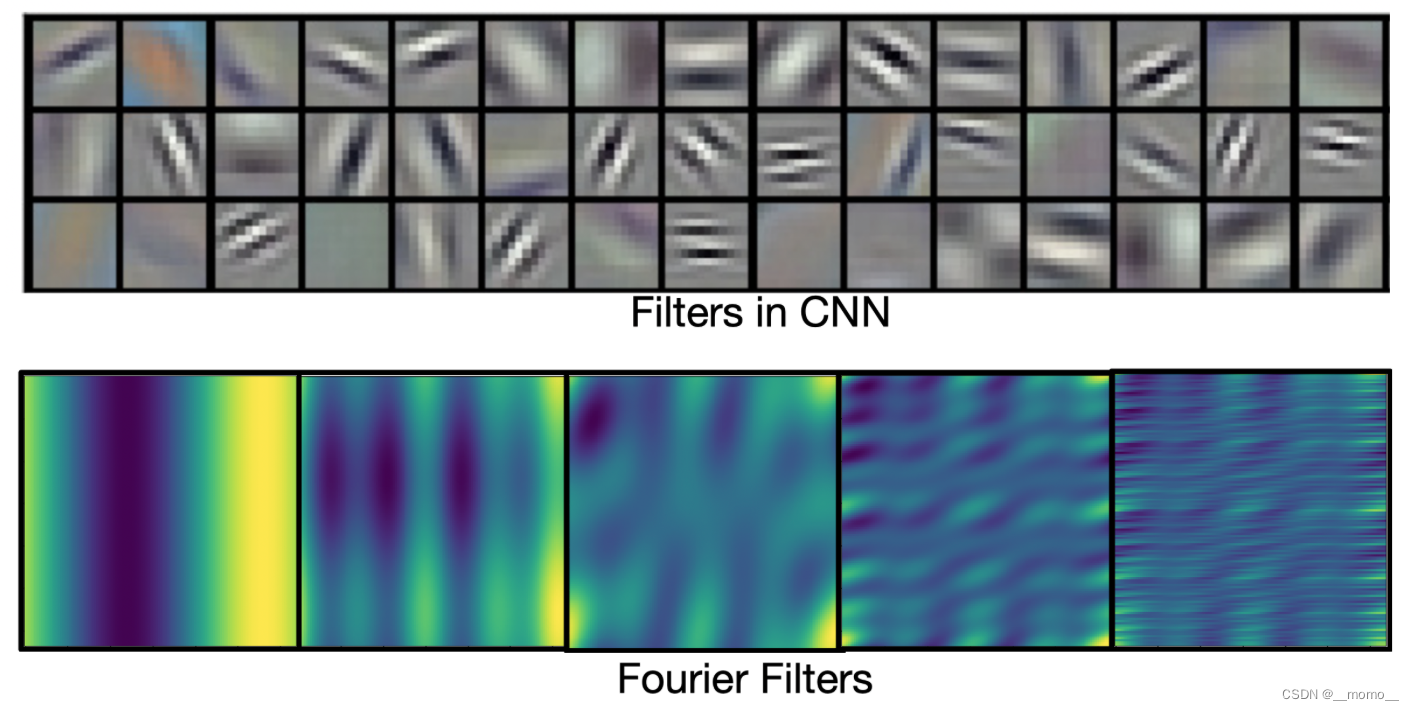






![[AIGC] Spring中的SPI机制详解](https://img-blog.csdnimg.cn/direct/0a50f4c8f3554d86aa7d91504068b517.png)