435. 无重叠区间
435. 无重叠区间 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
贪心算法,依然是判断重叠区间 | LeetCode:435.无重叠区间_哔哩哔哩_bilibili
给定一个区间的集合
intervals,其中intervals[i] = [starti, endi]。返回 需要移除区间的最小数量,使剩余区间互不重叠 。示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]] 输出: 1 解释: 移除 [1,3] 后,剩下的区间没有重叠。示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ] 输出: 2 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。示例 3:
输入: intervals = [ [1,2], [2,3] ] 输出: 0 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。提示:
1 <= intervals.length <= 105intervals[i].length == 2-5 * 104 <= starti < endi <= 5 * 104
没看卡哥题解,自己的想法就是先把区间从小到大排序,具体就是比较区间的最左边的值,也就是区间的最小值,最小值小的排前面。然后遍历每个区间,将第i个区间的left和第i-1区间的right值比较大小,left<=right则没有重叠,反之则有重叠,count++:
class Solution { // 定义一个类Solution
public int eraseOverlapIntervals(int[][] intervals) { // 定义一个公有方法eraseOverlapIntervals,接受一个二维整数数组intervals作为参数,并返回一个整数值
Arrays.sort(intervals, (a,b)-> { // 使用Arrays.sort对intervals进行排序,排序规则是按照子数组的第一个元素升序排列
return Integer.compare(a[0],b[0]); // 比较两个子数组的第一个元素的大小,返回比较结果
});
int remove = 0; // 初始化变量remove为0,用于记录需要移除的重叠区间数量
int pre = intervals[0][1]; // 初始化变量pre为第一个区间的结束位置,用于记录上一个不重叠的区间的结束位置
for(int i = 1; i < intervals.length; i++) { // 循环遍历intervals数组,从第二个区间开始
if(pre > intervals[i][0]) { // 如果上一个区间的结束位置大于当前区间的开始位置,表示存在重叠
remove++; // 计数器remove加1,表示需要移除一个重叠区间
pre = Math.min(pre, intervals[i][1]); // 更新上一个不重叠区间的结束位置为当前区间的结束位置和上一个区间结束位置的较小值
}
else pre = intervals[i][1]; // 如果当前区间不与上一个区间重叠,则更新上一个不重叠区间的结束位置为当前区间的结束位置
}
return remove; // 返回需要移除的重叠区间数量
}
}
763.划分字母区间
763. 划分字母区间 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
贪心算法,寻找最远的出现位置! LeetCode:763.划分字母区间_哔哩哔哩_bilibili
给你一个字符串
s。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是
s。返回一个表示每个字符串片段的长度的列表。
示例 1:
输入:s = "ababcbacadefegdehijhklij" 输出:[9,7,8] 解释: 划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。 每个字母最多出现在一个片段中。 像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的,因为划分的片段数较少。示例 2:
输入:s = "eccbbbbdec" 输出:[10] 提示:
1 <= s.length <= 500s仅由小写英文字母组成
这个题第一想法就是双指针法,一个指针i指向区间开头的字母,另外一个指针j从区间最左边向右遍历,直到找到和第一个字母相同的字母,返回这个字母的下标,然后指针i向右移动一位,指针j从原地右移;如果没找到,就把左边的指针i向后移动一位,重复上述过程。指针i和指针j的位置就是需要切割的位置。
写完发现好乱。。。。还是看卡哥题解吧。。
🤓看了卡哥题解后发现我有2点没弄清楚所以导致很乱:
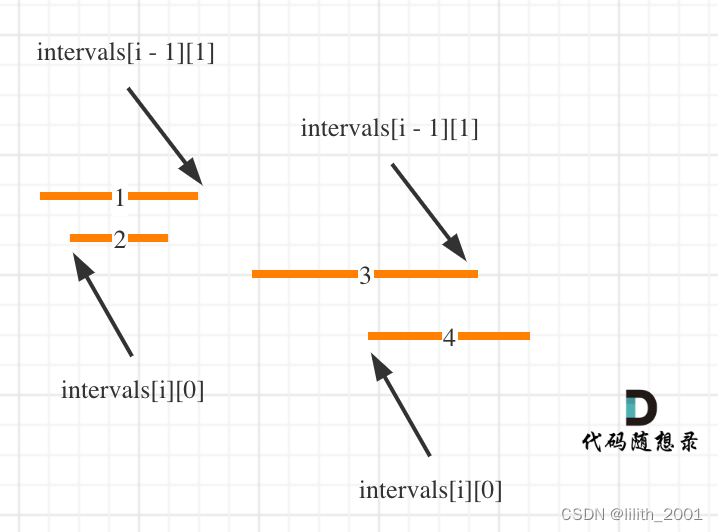
1、区间与区间之间一定是不重合的,所以下一个区间起始的位置一定在上一个区间结束位置的后面
2、我最大的问题在于用双指针法很糊。不建议用双指针法,直接标出每个字母的下标,某字母下标最大的位置就是这个字母最远的位置,必须包括在同一个区间内,如图:

卡哥还有一点很巧妙的就是将字母转换成数字做减法,整体代码如下:
class Solution {
public List<Integer> partitionLabels(String S) {
// 创建一个列表来存储分区的长度
List<Integer> list = new LinkedList<>();
// 初始化一个数组来存储每个字符在字母表中的最后出现位置的索引
int[] edge = new int[26];
// 将输入字符串转换为字符数组
char[] chars = S.toCharArray();
// 遍历字符串的字符,存储每个字符的最后出现位置的索引
for (int i = 0; i < chars.length; i++) {
edge[chars[i] - 'a'] = i;
}
// 初始化变量来跟踪当前索引和当前分区的最后一个索引
int idx = 0;
int last = -1;
// 再次遍历字符串的字符
for (int i = 0; i < chars.length; i++) {
// 更新当前分区的最后一个索引
idx = Math.max(idx, edge[chars[i] - 'a']);
// 如果当前索引等于当前分区的最后一个索引,
// 这意味着我们已经到达当前分区的末尾
if (i == idx) {
// 将当前分区的长度添加到列表中
list.add(i - last);
// 更新当前分区的最后一个索引
last = i;
}
}
// 返回包含分区长度的列表
return list;
}
}
56. 合并区间
56. 合并区间 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
贪心算法,合并区间有细节!LeetCode:56.合并区间_哔哩哔哩_bilibili
以数组
intervals表示若干个区间的集合,其中单个区间为intervals[i] = [starti, endi]。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
先按左边界的值排序:
发现重合后其实只需要更新右边界:
// 更新最右边界为当前区间右边界和原最右边界的较大值
rightmostRightBound = Math.max(rightmostRightBound, intervals[i][1]);综合代码:
class Solution {
public int[][] merge(int[][] intervals) {
// 创建一个列表来存储合并后的区间
List<int[]> res = new LinkedList<>();
// 按照区间的左边界进行排序
Arrays.sort(intervals, (x, y) -> Integer.compare(x[0], y[0]));
// 初始化 start 为第一个区间的左边界
int start = intervals[0][0];
// 初始化最右边界为第一个区间的右边界
int rightmostRightBound = intervals[0][1];
// 遍历区间数组
for (int i = 1; i < intervals.length; i++) {
// 如果当前区间的左边界大于当前最右边界
if (intervals[i][0] > rightmostRightBound) {
// 将当前区间合并到结果中,并更新 start 和最右边界
res.add(new int[]{start, rightmostRightBound});
start = intervals[i][0];
rightmostRightBound = intervals[i][1];
} else {
// 更新最右边界为当前区间右边界和原最右边界的较大值
rightmostRightBound = Math.max(rightmostRightBound, intervals[i][1]);
}
}
// 添加最后一个合并后的区间到结果中
res.add(new int[]{start, rightmostRightBound});
// 将结果列表转换为数组并返回
return res.toArray(new int[res.size()][]);
}
}
738.单调递增的数字
738. 单调递增的数字 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
贪心算法,思路不难想,但代码不好写!LeetCode:738.单调自增的数字_哔哩哔哩_bilibili
注意点:
1、这个题要注意从后往前遍历。
2、传进来的数值是int类型,为了方便各个位上的数值比较大小,将int类型转为字符串。
3、start记录位置,start后面的都赋值为9才能得到最大值
4、start初始为s的长度而不是0,为的就是避免s=1234这种情况出现时,再走for (int i = start; i < s.length(); i++) {
chars[i] = '9'; 的逻辑将s变成1999.
class Solution {
public int monotoneIncreasingDigits(int n) {
// 将输入的整数转换为字符串
String s = String.valueOf(n);
// 将字符串转换为字符数组
char[] chars = s.toCharArray();
// 初始化变量 start 为字符串的长度
int start = s.length();
// 从倒数第二位开始向前遍历字符数组
for (int i = s.length() - 2; i >= 0; i--) {
// 如果当前字符大于后面一位字符
if (chars[i] > chars[i + 1]) {
// 将当前字符减去1,并更新 start 的值为当前位置的后一位
chars[i]--;
start = i + 1;
}
}
// 将 start 位置后的所有字符设为 '9'
for (int i = start; i < s.length(); i++) {
chars[i] = '9';
}
// 将字符数组转换为整数并返回
return Integer.parseInt(String.valueOf(chars));
}
}