1 0-1背包介绍【每件物品只能拿1件或者不拿】
1.1 简介


贪心是不可以的!!!

1.2 状态 及状态转移


转移解释:要么不选 则上一个直接转移过来【dp[i-1][j]】,要么是选这个之后体积为j 则上一个对应的就是【dp[i-1][j-wi] + v[i]】 选上这个之后价值叫上哦!!1
1.3 代码

n,v= list(map(int,input().split()))
w = [0]
value = [0]
for i in range(n):
w_v = list(map(int,input().split()))
w.append(w_v[0])
value.append((w_v[1]))
# print(w)
# print(value)
'''容量总共为V
不超过v的时候价值最大
求最大价值--是矩阵中的值,那么还有两个指标分别是 物品数和容量
dp[i][j]表示前i个物品当体积为j时对应的价值'''
'''找到状态之后 想状态转移方程:
如果第i个物品不拿 dp[i][j] = dp[i-1][j]
如果第i个物品拿 dp[i][j] = dp[i-1][j-w[i]]+value[i]
要最大的价值 则选最大的 决定拿还是不拿'''
dp = [[0]*(v+1) for i in range(n+1)]
for i in range(1,n+1):
for j in range(1,v+1):
if j>=w[i]: # 说明存在第i个拿出来这种情况
dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]]+value[i])
else:
dp[i][j] = dp[i-1][j]
print(dp[n][v])
2 滚动数组优化
发现在上方的代码中 更新第i行只用到了i-1行的数据,所有可以把空间压缩为2
然后对代码做以下改变即可

3 完全背包【每件物品可以拿0件1件2件一直到无数件】
3.1 定义
每个物品可以不拿或者拿一件 两件。。。这样

有三个参数了现在,依次枚举i,j,k 三重循环时间代价太大了

怎么优化时间呢?

![]()
3.2 代码实现

n,v= list(map(int,input().split()))
w = [0]
value = [0]
for i in range(n):
w_v = list(map(int,input().split()))
w.append(w_v[0])
value.append((w_v[1]))
# print(w)
# print(value)
dp = [[0]*(v+1) for i in range(n+1)]
for i in range(1,n+1):
for j in range(1,v+1):
if j>=w[i]: # 说明存在第i个拿出来这种情况
dp[i][j] = max(dp[i-1][j], dp[i][j-w[i]]+value[i])
else:
dp[i][j] = dp[i-1][j]
print(dp[n][v])
4 多重背包【0-1背包和完全背包的结合体】
4.1 定义

每种物品可是可以多拿但是有一个上限!!

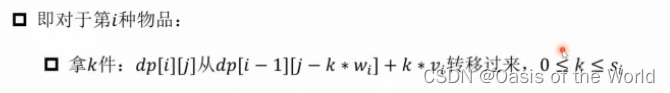
不拿的情况也包含在上面的那个式子里了,所以更新值只需要 和自己比 留下最大的即可!!!
完全背包没有办法控制上限,所以我们只能老老实实的三重循环。。。
4.2 三重循环代码
n,v= list(map(int,input().split()))
w = [0]
value = [0]
s = [0]
for i in range(n):
w_v_s = list(map(int,input().split()))
w.append(w_v_s[0])
value.append(w_v_s[1])
s.append(w_v_s[2])
# print(w)
# print(value)
'''容量总共为V
不超过v的时候价值最大
求最大价值--是矩阵中的值,那么还有两个指标分别是 物品数和容量
dp[i][j]表示前i个物品当体积为j时对应的价值'''
'''找到状态之后 想状态转移方程:
如果第i个物品不拿 dp[i][j] = dp[i-1][j]
如果第i个物品拿 dp[i][j] = dp[i-1][j-w[i]]+value[i]
要最大的价值 则选最大的 决定拿还是不拿'''
dp = [[0]*(v+1) for i in range(n+1)]
for i in range(1,n+1):
for j in range(1,v+1):
for m in range(0, min(s[i],j//w[i])+1):
# if j >= m*w[i]: # 说明存在第i个拿出来这种情况
dp[i][j] = max(dp[i][j], dp[i-1][j-m*w[i]]+m*value[i])
# 和0-1背包的区别就是dp[i-1][j-w[i]]变成了dp[i][j-w[i]]
# else:
# dp[i][j] = dp[i][j]
print(dp[n][v])4.3 二进制优化后代码

新策略:二进制的拆si !!!!!!!!!!!!!
普通拆发:

二进制的拆法:



##二进制优化
import sys
def put(_w, _v):
for j in range(v, _w - 1, -1):
dp[j] = max(dp[j], dp[j-_w] + _v)
n, v = map(int, sys.stdin.readline().split())
dp = [0]*(v + 1)
for _ in range(n):
weight, value, i = map(int, sys.stdin.readline().split())
tmp = 1
while i >= tmp:
put(weight * tmp, value * tmp)
i -= tmp
tmp <<= 1
if i > 0:
put(weight * i, value * i)
print(dp[v])5 二维费用背包
5.1 定义

 、
、
状态转移方程:

空间上受不了,用滚动数组

可以把i删掉
5.2 代码

N,V,M=map(int, input().split())
dp = [[0]*(M+1) for i in range(V+1)]
for i in range(1,N+1):
vi,mi,wi = map(int, input().split())
for j in range(V,vi-1,-1):
for k in range(M,mi-1,-1):
#dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j-vi][k-mi]+wi)
dp[j][k] = max(dp[j][k], dp[j-vi][k-mi]+wi)
print(dp[V][M])6 分组背包

很像01背包
'''
分组背包:
每组中只能选择一个物品
状态转移方程与0-1背包一样,唯一的区别是:在更新状态时要多与自己比较一次
不用一维滚动数组优化时,遍历顺序是每组,组中每个元素,背包容量
使用一维滚动数组优化时,遍历顺序是每组,背包容量,组中每个元素(可防止组中元素被选择多次)
'''
##1、没有优化空间
N,V = map(int,input().split())
dp = [[0]*(V+1) for i in range(N+1)]
# dp[i][j]表示前i组物品体积不超过j的最大价值
#最终的答案dp[N][V]
for i in range(1,N+1): # 对于每个组
s = int(input())
for q in range(s): # 对于每个组中的每个物品
w,v = map(int,input().split()) #获取每个物品的质量与价值
for j in range(0,V+1): #对于当前背包容量
if j< w: #分组背包更新状态时,要比其他背包多一次比较,即要与本身做一次比较
dp[i][j] = max(dp[i][j], dp[i-1][j])
else:
dp[i][j] = max(dp[i][j],dp[i-1][j],dp[i-1][j-w] + v)
print(dp[N][V])
#2.两行滚动数组优化
N,V = map(int,input().split())
dp = [[0]*(V+1)for i in range(2)]
for i in range(1,N+1):#对于每个组
s = int(input())
for _ in range(s): #对于每个组中的每个物品
w,v = map(int,input().split()) #获取每个物品的质量与价值
for j in range(1,V+1): #对于当前背包容量
if j< w: #分组背包更新状态时,要比其他背包多一次比较,即要与本身做一次比较
dp[i%2][j] = max(dp[i%2][j], dp[(i-1)%2][j])
else:
dp[i%2][j] = max(dp[i%2][j],dp[(i-1)%2][j],dp[(i-1)%2][j-w] + v)
print(dp[N%2][V])
#3 一维滚动数组优化 YYDS
N,V = map(int,input().split())
dp = [0]*(V+1)
for i in range(1,N+1):#对于每个组
s = int(input())
group = []
for _ in range(s): #对于每个组中的每个物品
group.append([*map(int,input().split())])
#分组包采用一维滚动数组时,需先遍历背包容量,再遍历每组每个物品的质量与价值,否则会出现一组中的物品被选择多次的情况
for j in range(V,-1,-1): #对于当前背包容量
for w,v in group: #获取每个物品的质量与价值
if j>=w: #背包容量不能小于物品质量,不然装不了
#分组背包更新状态时,要比其他背包多一次比较,即要与本身做一次比较
dp[j] = max(dp[j],dp[j-w] + v)
print(dp[V])