LeetCode-1766. 互质树【树深度优先搜索广度优先搜索数组数学数论】

news2025/2/28 3:55:46

LeetCode-1766. 互质树【树深度优先搜索广度优先搜索数组数学数论】

题目描述：
解题思路一：DFS 中记录节点值的深度和编号，回溯写法。关键点是1 <= nums[i] <= 50
解题思路二：0
解题思路三：0

题目描述：

给你一个 n 个节点的树（也就是一个无环连通无向图），节点编号从 0 到 n - 1 ，且恰好有 n - 1 条边，每个节点有一个值。树的根节点为 0 号点。

给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值，edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。

当 gcd(x, y) == 1 ，我们称两个数 x 和 y 是互质的，其中 gcd(x, y) 是 x 和 y 的最大公约数。

从节点 i 到根最短路径上的点都是节点 i 的祖先节点。一个节点不是它自己的祖先节点。

请你返回一个大小为 n 的数组 ans ，其中 ans[i]是离节点 i 最近的祖先节点且满足 nums[i] 和 nums[ans[i]] 是互质的，如果不存在这样的祖先节点，ans[i] 为 -1 。

示例 1：
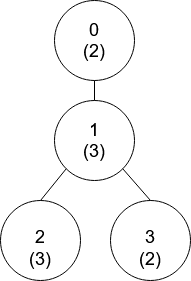
在这里插入图片描述
输入：nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
输出：[-1,0,0,1]
解释：上图中，每个节点的值在括号中表示。

节点 0 没有互质祖先。
节点 1 只有一个祖先节点 0 。它们的值是互质的（gcd(2,3) == 1）。
节点 2 有两个祖先节点，分别是节点 1 和节点 0 。节点 1 的值与它的值不是互质的（gcd(3,3) == 3）但节点 0 的值是互质的(gcd(2,3) == 1)，所以节点 0 是最近的符合要求的祖先节点。
节点 3 有两个祖先节点，分别是节点 1 和节点 0 。它与节点 1 互质（gcd(3,2) == 1），所以节点 1 是离它最近的符合要求的祖先节点。
示例 2：

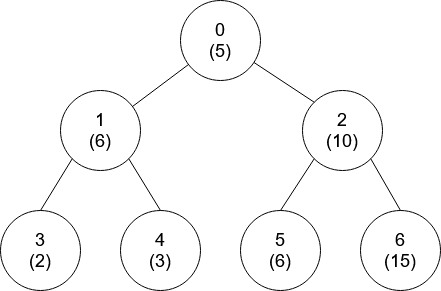
输入：nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出：[-1,0,-1,0,0,0,-1]

提示：

nums.length == n
1 <= nums[i] <= 50
1 <= n <= 10⁵
edges.length == n - 1
edges[j].length == 2
0 <= uj, vj < n
uj != vj

解题思路一：DFS 中记录节点值的深度和编号，回溯写法。关键点是1 <= nums[i] <= 50

对于节点 x，我们需要计算节点值与 nums[x] 互质的最近祖先节点是哪个。

最暴力的做法是，枚举 x 的所有祖先节点。但如果这棵树是一条链，枚举 x 的所有祖先节点需要 O(n) 的时间，每个点都这样枚举的话，总共需要 O(n²) 的时间，太慢了。

注意到，所有节点的节点值都不超过 50，我们可以枚举 [1,50] 中与 nums[x] 互质的数。由于要计算的是「最近」祖先，对于节点值相同的祖先，只需枚举深度最大的。因此，对于节点 x，我们至多枚举它的 50 个祖先。这样总共只需要 O(nU) 的时间，其中 U=50。

具体来说，我们需要在递归这棵树的同时，维护两组信息：

valDepth 数组。其中 valDepth[j] 保存节点值等于 j 的最近祖先的深度。
valNodeId 数组。其中 valNodeId[j] 保存节点值等于 j 的最近祖先的节点编号。

设当前节点值为 val=nums[x]，我们枚举 [1,50] 中与 val互质的数字 j，计算出 valDepth[j] 的最大值，及其对应的节点编号，即为答案 ans[x]。

代码实现时，可以预处理 [1,50]中有哪些数对是互质的。

# 预处理：coprime[i] 保存 [1, MX) 中与 i 互质的所有元素
MX = 51
coprime = [[j for j in range(1, MX) if gcd(i, j) == 1]
            for i in range(MX)]
class Solution:
    def getCoprimes(self, nums: List[int], edges: List[List[int]]) -> List[int]:
        n = len(nums)
        g = [[] for _ in range(n)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)

        ans = [0] * n
        val_depth_id = [(-1, -1)] * MX # 包含深度和节点编号
        def dfs(x: int, fa: int, depth: int) -> None:
            val = nums[x] # x 的节点值
            # 计算与 val 互质的祖先节点值中，节点深度最大的节点编号
            ans[x] = max(val_depth_id[j] for j in coprime[val])[1]
            tmp = val_depth_id[val]  # 用于恢复现场
            val_depth_id[val] = (depth, x)  # 保存 val 对应的节点深度和节点编号
            for y in g[x]:
                if y != fa:
                    dfs(y, x, depth + 1)
            val_depth_id[val] = tmp # 恢复现场
        dfs(0, -1, 0)
        return ans