LeetCode 热题 100 题解（二）：双指针部分（1）

题目一：移动零（No. 283）

题目链接：https://leetcode.cn/problems/move-zeroes/description/?envType=study-plan-v2&envId=top-100-liked

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums =[0,1,0,3,12]
输出:[1,3,12,0,0]

示例 2:

输入: nums =[0]
输出:[0]

提示:

1 <= nums.length <= 104
231 <= nums[i] <= 231 - 1

题解

本题要求是将所有的 0 移动到数组的末尾，同时要保证原本的顺序，直接顺着这个思路去实现是很困难的，此时可以换一个思路：将所有非零的数字都移到最前面就可以了，这样就可以很容易的保证移动之后的顺序，具体可以看下面的动画演示。

在这里插入图片描述

图片来源：王尼玛

首先声明两个指针，一个指针去遍历数组查找非零的数据，另一个指针去标明替换的位置，当指针 a 遍历到非零的元素，就与 b 指针进行替换的操作。

所以此时的思路就是两个指针分别去遍历，当 b 寻找到为 0 的节点就停住，等待 a 找到非零的节点进行替换的操作，写出代码是这样的：

class Solution {
    public void moveZeroes(int[] nums) {
        int j = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0 && nums[j] == 0) {
            // 如果找到了非零的节点就进行替换的操作
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
                j++;
            }
            if (nums[j] != 0) j++; // 如果不是 0，继续向后寻找
        }
    }
}

但其实不管 j 的位置是否为 0 其实都可以进行替换的操作，这里先给出代码：

class Solution {
    public void moveZeroes(int[] nums) {
        int j = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0) { // 找到了非零的节点
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
                j++;
            }
        }
    }
}

这样的写法其实就是融合了上面的两种情况，如果 nums[j] != 0 的时候也执行替换的操作

在 nums[j] != 0 且 nums[i] != 0 的情况下执行替换的操作的情况，只有一种可能 就是i == j 的情况，此时执行的就是自身和自身替换，然后同时后移一位

我们在 if 语句中加一个语句来验证这个结论：if (nums[j] != 0) System.*out*.println(i == j);
测试用例：1, 3, 4, 0, 0, 1, 0, 3, 12，此时输出的为 true true true

我们来多测试几组试一下：1, 4, 0, 0, 1, 0, 3, 12，此时输出的是 true true

那 1, 0, 0, 1, 0, 3, 12 呢？猜一下也能知道是 1

这些是执行自身替换的次数，这种行为会在 遇到第一个0的时候 停止，在遇到 0 之后，j 就会跟不上 i 的速度，**从而一定会留在为 0 的位置上，**这个大家举几个案例就可以很轻松的看出来，j 一定会留在为 0 的位置上；相较于第一种方法，第二种简化了判断的逻辑，执行速度比第一种快得多。

为了少执行替换操作，可以在方法上执行这个逻辑

  			int temp = 0;
        for(int i = 0; i < nums.length; i++) {
            if (nums[i] == 0) {
                temp = i;
                break;
            }
        } 
        int j = temp;

先找到为零的节点再执行下面的代码，但其实这样优化的意义不是特别大，但对理解这个解法比较有帮助。

题目二：盛水最多的容器（No. 11）

题目链接：https://leetcode.cn/problems/container-with-most-water/description/?envType=study-plan-v2&envId=top-100-liked

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

示例 1：
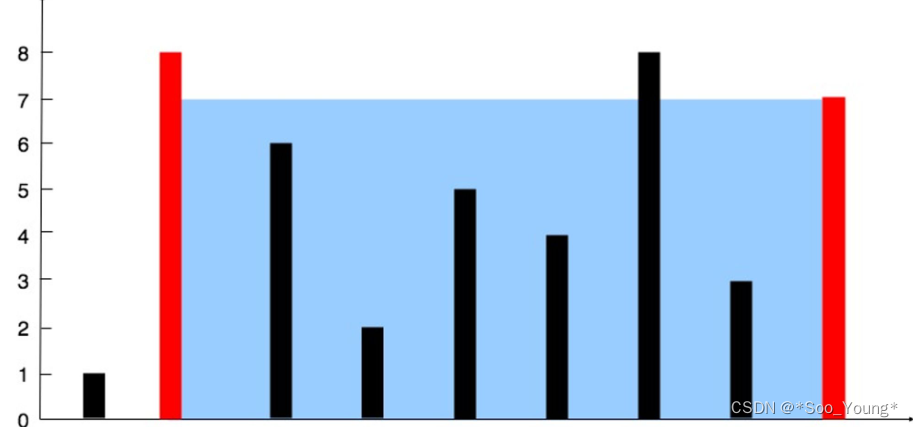
在这里插入图片描述

输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

n == height.length
2 <= n <= 105
0 <= height[i] <= 104

题解

为了求容器的容量，本题需要考虑到两个因素，分别是两个容器壁的最低高度，第二个是两个容器壁之间的距离，这两个限制条件很难去同时兼顾到，所以本题首先想到的方式就是穷举法，将所有可能出现的情况都列举出来，一定不要忽视穷举法，很多好的方法都是在穷举的基础上优化来的。

穷举的思路就是指定两个指针，left 和 right，left 首先指向 0，right 指针指向数组的末尾，然后对 right 进行递减的操作，知道 right == left 结束此次循环，然后执行 left++，再次从末尾去循环 right。

在遍历中不断去取得容量，直到遍历完成后输出最终的容量。

此时，思考一个问题，如果我发现 height[left] < height[right] ，还有必要去遍历整个数组嘛？

如果 height[left] < height[right] 那此时的容量就是 height[left] * (right - left) ，此时我去移动 right，那只有两种情况：

高度比刚刚的还高或者高度比刚刚的还低，无论是哪种情况，得到的结果 一定是小于最初的情况的；所以得出一个结论，如果我发现 height[left] < height[right] 就直接结束本次遍历即可

class Solution {
    public int maxArea(int[] height) {
        int res = 0;
        for (int left = 0; left < height.length - 1; left++) {
            int right = height.length - 1;
            while (right > left) { // 循环遍历 right
                int temp = (right - left) * Math.min(height[left], height[right]);
                res = Math.max(temp, res);
                if (height[left] < height[right]) break;
                right--;
            } 
        }
        return res;
    }
}

写出代码就是这样子的。

但是上面的解法时间复杂度仍然非常高，left 要遍历完整个数组，那有没有可能提前结束呢？

反过来去思考这道题目，其实我固定 right，然后去从头遍历 left 也是可以的，终止条件就变为了 height[right] < height[left]

那此时就有一个新的思路，两个指针分别指向开头和结尾，如果我发现左边的比较矮，我就移动左指针，反之则移动右指针，这样就同时运用到了固定 left 和固定 right 两种情况的限制条件，从而进一步的优化解法：

class Solution {
    public int maxArea(int[] height) {
        int left = 0;
        int right = height.length - 1;
        int res = 0;
        while (left < right) {
            int h = Math.min(height[left], height[right]);
            int temp = (right - left) * h;
            res = Math.max(temp, res);
            if (height[left] <= height[right]) {
            // 如果左边的低
                left++;
            } else {
            // 如果右边的低
                right--;
            }
        }
        return res;
    }
}

题目三：三数之和（No. 15）

题目链接：https://leetcode.cn/problems/3sum/description/?envType=study-plan-v2&envId=top-100-liked

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

**注意：**答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

提示：

3 <= nums.length <= 3000
105 <= nums[i] <= 105

题解

本题中给出一个数组，求数组中和为 0 的三元组，且要求 不能重复。

之前题解中我们讲解过两数之和这道题目，本题如果固定一个元素，然后本题就转化为在剩余的元素中，找两个数字，其和为 0 - 固定的数字 。这样就把三树之和转化为了两数之和来求解，这是求解本题的大致思路。

但是与两数之和不同的是，本题中要求了去重

为了将相同的元素聚集在一起，就可以执行排序的方法，通过 Arrays.sort() 方法排序，可以将所有相同的元素聚集在一起，方便后续进行去重的操作。

首先来考虑第一个元素的选取，经过排序之后，数组是这样的：

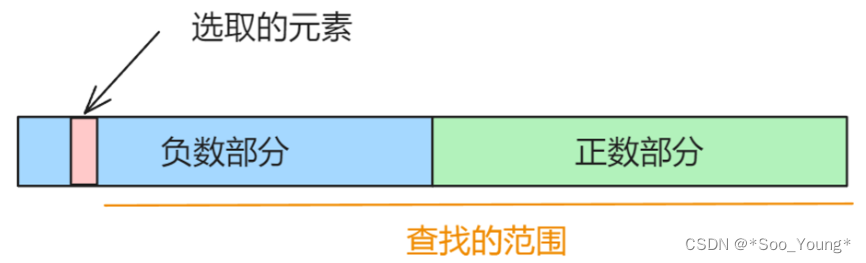
在这里插入图片描述

当选定一个元素后，剩下两个元素的查找范围就是下一个一直到末尾（为了不出现重复的情况），在这种情况下选定的这个元素就 **一定是负数，**因为如果选定的是正数的话，在查找范围内无法形成和为 0 的情况。

那此时第一个元素的范围就确定了：

for (int i = 0; i < nums.length; i++) {
	if (nums[i] > 0) {
	    return res;
	}
	if (i > 0 && nums[i] == nums[i - 1]) {
	    continue;
	}
	// 其他的逻辑
}

上面代码展示的就是遍历第一个元素的逻辑，首先要保证 i 不会越界，其次要保证 nums[i] 是小于等于零的，当发现 nums[i] > 0 的时候就说明本次的查找已经结束了，直接将 res 返回；第二段 if 进行去重的，就是如果发现 nums[i] == nums[i - 1] （和上一个相同），此时就直接遍历下一个元素。

然后就是在剩余的部分中找到两个数，使得它们三个的和为 0，当然可以使用前面的哈希，但这里因为经过了排序，我们使用一个新的双指针方法来解决：

首先指定两个指针，来规范查找的范围：

int left = i + 1;
int right = nums.length - 1;

此时的和为： nums[left] + nums[right] + nums[i] ，然后去判断这个和是大于、小于还是等于 0。

如果发现大于零，就说明取得值太大了，此时左移 right 指针
如果发现小于零，则说明取得值太小了，此时右移 left 指针
如果恰好等于零就将其存储下来

      while(left < right) {
          int temp = nums[left] + nums[right] + nums[i];
          if (temp > 0) {
              right--;
          } else if (temp < 0) {
              left++;
          } else {
		          res.add(Arrays.asList(nums[i], nums[left], nums[right])); 
              // 去重逻辑
              right--;
              left++;
          }
      }

在恰好等于的情况需要考虑去重的逻辑，否则就会出现重复的情况，此时就需要移动指针直到 nums[left] != nums[left - 1] 同时 nums[right] != nums[right + 1] ，可以通过 while 循环来解决：

      while (left < right && nums[left] == nums[left + 1]) {
          left++;
      }
      while (right > left &&  nums[right] == nums[right - 1]) {
          right--;
      }

此时整个流程就完成了，这里给出完整的代码：

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(nums);
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] > 0) {
                return res;
            }
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            // 先固定一个，剩下和二维的比较类似了
            int left = i + 1;
            int right = nums.length - 1;
            while(left < right) {
                int temp = nums[left] + nums[right] + nums[i];
                if (temp > 0) {
                    right--;
                } else if (temp < 0) {
                    left++;
                } else {
                    res.add(Arrays.asList(nums[i], nums[left], nums[right])); 
                    while (left < right && nums[left] == nums[left + 1]) {
                        left++;
                    }
                    while (right > left &&  nums[right] == nums[right - 1]) {
                        right--;
                    }
                    right--;
                    left++;
                }
            }
        }
        return res;
    }
}