目录
- 题目
- 题解
- 贪心算法
- 双指针
- 解题思路
- 暴力破解法
- 双指针
- 总结
题目
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
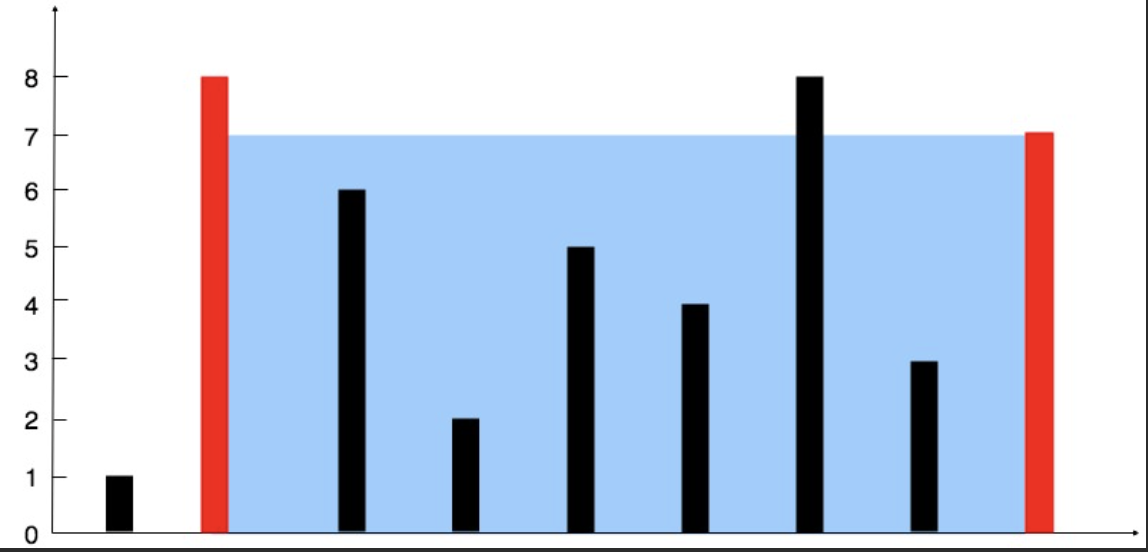
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
提示:
n == height.length
2 <= n <= 105
0 <= height[i] <= 104
题解
贪心算法
贪心算法是一种常见的算法思想,用于在求解最优化问题时做出每一步的局部最优选择,从而达到全局最优的目标。贪心算法的基本思路是,在每一步都做出当前情况下的最优选择,并希望通过这种局部最优选择的组合来达到全局最优解。
贪心算法的解题思路一般包括以下几个步骤:
-
确定问题的最优子结构:贪心算法通常适用于具有最优子结构的问题,即问题的最优解可以通过一系列局部最优解的组合得到。
-
定义贪心选择策略:根据问题的特点,确定每一步的最优选择是什么。这个选择应该是局部最优的,并且希望通过这个选择能够达到全局最优解。
-
构造解的过程:通过贪心选择策略,逐步构建出问题的解。在每一步选择后,更新问题的状态,进而影响后续步骤的选择。
-
验证解的正确性:在构造解的过程中,需要验证每一步的选择是否满足问题的约束条件。同时,需要证明通过贪心选择策略得到的解是最优解。
需要注意的是,贪心算法并不适用于所有问题,因为它只关注当前局部最优解,并没有考虑到全局的影响。在某些情况下,贪心算法可能会得到次优解或者无法得到可行解。因此,在应用贪心算法时需要仔细分析问题的特点,确保贪心选择策略能够得到正确的解。
一些经典的使用贪心算法的问题包括:
零钱兑换问题:给定一定面额的硬币,求解如何用最少的硬币数凑出给定的金额。
区间调度问题:给定一组区间,求解如何选择最多的不重叠区间。
跳跃游戏问题:给定一个非负整数数组,每个元素表示在当前位置能够跳跃的最大步数,求解是否能够到达数组的最后一个位置。
在解决这些问题时,贪心算法能够提供高效的解决方案。但对于不同的问题,贪心选择策略的选择和实现方式可能会有所不同,需要根据具体问题进行分析和设计。
双指针
双指针算法是一种常见的算法技巧,它通过使用两个指针在数组或链表中同时移动,以解决一些特定的问题。双指针算法通常用于处理有序数组或链表的问题,可以在O(n)的时间复杂度内解决一些问题,而不需要额外的空间复杂度。
双指针算法的解题思路一般包括以下几个步骤:
初始化指针:通常情况下,会初始化两个指针,一个指向数组或链表的起始位置,另一个指向末尾位置或者某个特定位置。
移动指针:根据问题的要求,移动指针的位置。可以根据当前指针指向的元素值或者某种条件来决定指针的移动方式。
判断条件:在移动指针的过程中,根据题目要求或者特定的条件,判断是否满足某种条件。
更新解或结果:根据判断条件的结果,更新解或者结果。
双指针算法常见的题型包括:
快慢指针:使用两个指针,一个快指针每次移动两步,一个慢指针每次移动一步。常用于判断链表是否存在环、找到链表的中间节点等问题。
左右指针:在有序数组中,使用两个指针分别指向数组的左右两端,根据数组的性质移动指针,以快速搜索或者判断满足条件的元素。
对撞指针:在有序数组中,使用两个指针分别从数组的两端向中间移动,根据数组的性质移动指针,以快速搜索或者判断满足条件的元素。
滑动窗口:使用两个指针构成一个窗口,在数组或字符串中滑动窗口,根据窗口的性质移动指针,以求解最优解或者满足特定条件的解。
一些经典的使用双指针算法的问题包括:
两数之和:给定一个有序数组和一个目标值,找出数组中和为目标值的两个数的索引。
反转数组:给定一个数组,将数组中的元素反转。
链表相交:给定两个链表,判断两个链表是否相交,并找到相交的节点。
最长回文子串:给定一个字符串,找到字符串中最长的回文子串。
双指针算法能够提供高效的解决方案,但需要根据具体问题进行分析和设计,选择合适的指针移动策略和判断条件。
解题思路
暴力破解法
首先拿到这个题目,第一时间想到就是暴力破解法。拿每数组中任意一个数和其他的数组成容器,暴力循环直到找到最大的那个数。

public int maxArea(int[] height) {
int i = 0;
int max = Integer.MIN_VALUE;
while(i < height.length - 1) {
for (int j = height.length - 1; j > i; j --) {
// 这里做了一点小优化,如果说最后面的那个数 height[j] >= height[i]的话就没必要继续往左边走了,因为往左边的数比height[i]大或小都没有意义了,由于木桶效应,决定木桶装水容量的应该是最小的那块木板。所以容器的容量最大应该就是两边都是高度都是height[i]。所以 height[j] >= height[i] 已经取到了左边高度为height[i]的情况下,容量最大也就是height[i] * (j - i) .
if (height[j] >= height[i]) { // 如果没这段优化直接就会超时
max = Math.max(height[i] * (j - i), max);
break;
} else {
max = Math.max(height[j] * (j - i), max);
}
}
i ++;
}
return max;
}
看到下图明显可以知道,性能很差,肯定不应该这样去做。
双指针
贪心算法的核心思想就是要求我们每一步都是最优解,从而得出全局最优。我们创建两个指针,保证left 和right在移动的时候,每一步都是最优解,从而得出全局最优。
步骤 ①

步骤 ②
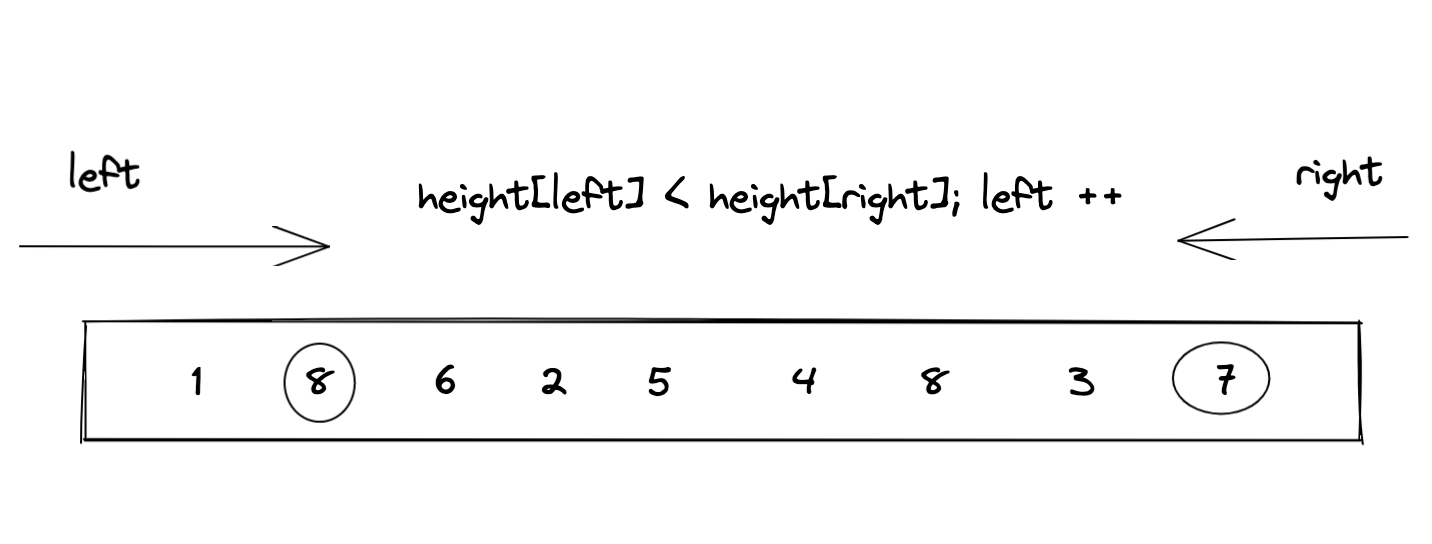
步骤③

public int maxAreaTwoPoint(int[] height) {
int i = 0, j = height.length - 1;
int max = Integer.MIN_VALUE;
while (i < j) {
if (height[i] < height[j]) {
max = Math.max(height[i] * (j - i), max);
i ++;
} else {
max = Math.max(height[j] * (j - i), max);
j --;
}
}
return max;
}
总结
贪心算法是一种常用的优化算法思想,它通过每一步选择当前最优解的策略,以期望达到全局最优解。贪心算法具有以下特点:贪心选择性质和局部最优解。贪心算法的步骤包括确定最优子结构、构建贪心选择、定义最优解的边界和迭代执行贪心选择。然而,贪心算法并不适用于所有问题,只适用于具备贪心选择性质的问题。在使用贪心算法时,需要仔细分析问题的特点,确保贪心选择的正确性,并进行适当的证明。贪心算法是一种简单而高效的算法思想,常用于解决优化问题。