IMU状态预积分噪声模型

根据之前的推导，得出了IMU状态预积分的测量模型，同时得到了噪声部分的定义公式，其中噪声部分罗列如下：

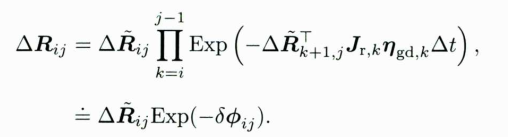
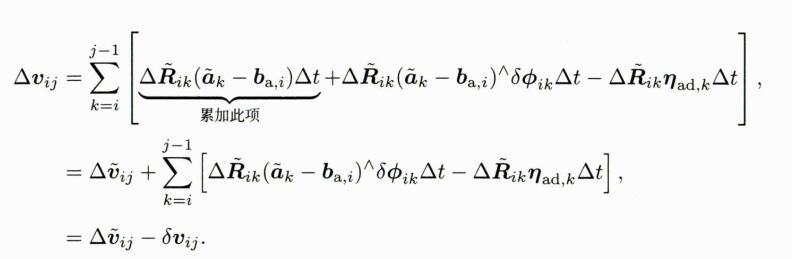
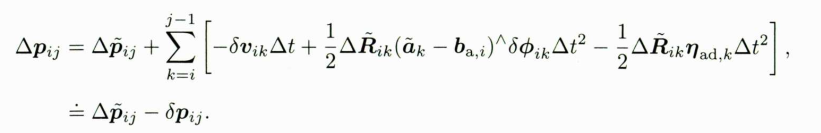
由于噪声项的定义比较复杂，需要将复杂的噪声项线性化，保留一阶系数，然后推导线性模型下的协方差矩阵变化。

旋转部分

首先从旋转部分的噪声开始

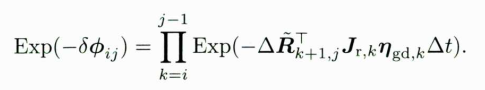
可以看到，作为随机变量的$\delta {\varphi }_{ij}$只和随机变量${\eta }_{gd}$有关，而且其它的都是确定的观测量。
线性化后取期望值时，由于${\eta }_{gd}$为白噪声，因此$\delta {\varphi }_{ij}$均值也为零。

为了分析它的协方差，需要对上面公式进行线性化。对两侧取Log,可得

上式又可以通过BCH进行线性近似。同时，由于内部的系数项$-△{\tilde{R}}_{k+1}^{\top }{J}_{r,k}{\eta }_{gd,k}△t$已经为噪声，接近于0，可以将BCH线性近似的右雅克比矩阵取为单位阵I，那么可以得到

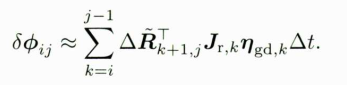
上式是高斯随机变量的线性组合，它的结果依然是高斯的。同时，由于预积分的累加特性，预积分观测量的噪声也会随着时间不断累加。

能否用第j-1时刻的噪声来计算第j时刻的噪声？如果可以，那么程序实现也会更简单。
答案：可以。
由于上式是累加形式的，因此很容易将其写成递推的形式：

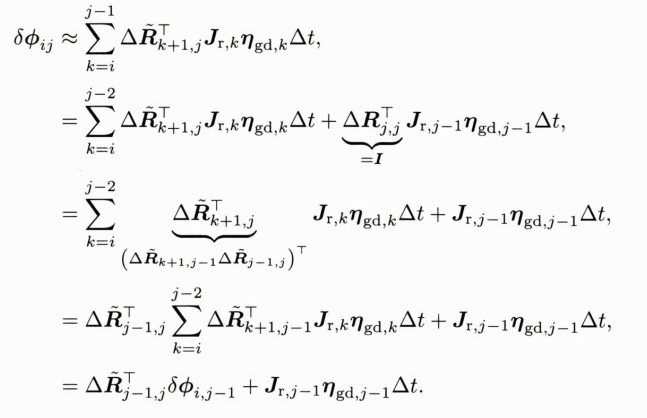
上式描述了如何从j-1时刻的噪声推断至j时刻。显然，这是一个线性系统。

设j-1时刻$\delta {\varphi }_{i，j-1}$的协方差为${\Sigma }_{j-1}$，${\eta }_{gd}$的协方差为${\Sigma }_{{\eta }_{gd}}$，那么：

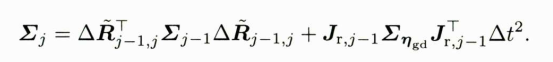
这表明预积分误差会随着数据累积而变大，预积分观测量也会变得越来越不确定。这和实际情况是相符的。

速度部分

接下来考虑速度。与旋转部分相同，速度部分也可以写成高斯噪声变量的线性组合形式：

它也可以写成累加的形式：

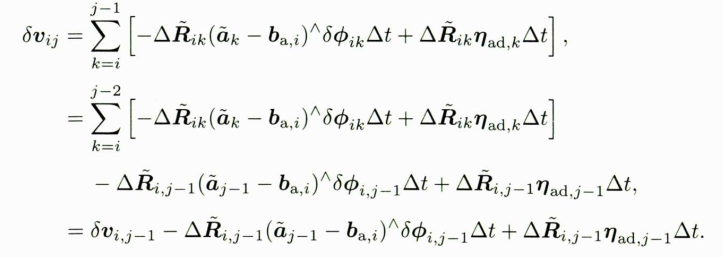
于是，$\delta v_{ij}$的协方差也可以根据累加系数来确定。

平移部分

对于平移部分也可以做速度部分同样的处理。直接列写平移部分噪声的累加形式：

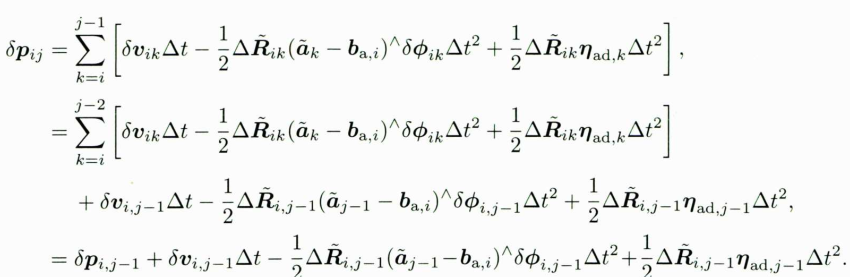
总结

上面推导了，如何从j-1时刻将噪声项递推至j时刻。

也可以将上面格式整理成矩阵形式。将三个噪声项合并成同一个：

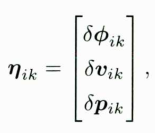
并且把IMU的零偏噪声定义为

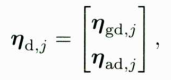
那么从${\eta }_{i，j-1}$至${\eta }_{i，j}$的递推式可以写作：

其中，系数矩阵$A_{j-1},B_{j-1}$为

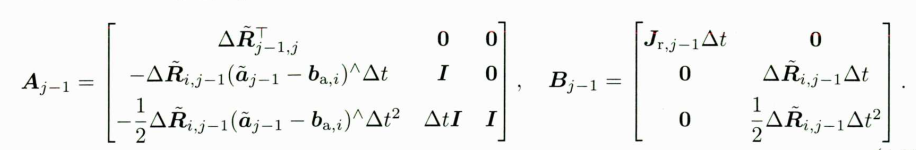
矩阵形式更清晰地显示了几个噪声项之间累积的递推关系。如果以协方差的形式来记录噪声，那么每次增加IMU观测时，噪声应该呈现逐渐增大的关系：

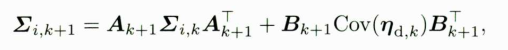
这里的Ak+1矩阵接近单位阵I，因此可以看成将噪声累加。
陀螺仪的噪声通过B矩阵进入旋转的观测量中，而加速度计的噪声则主要进入速度与平移估计中。