一句话总结:前两题白给,第三题树形DP有点难。
原题链接:198 打家劫舍

滚动数组直接秒了。
class Solution {
public int rob(int[] nums) {
int n = nums.length;
int first = 0, second = nums[0];
for (int i = 2; i <= n; ++i) {
int tmp = Math.max(first + nums[i - 1], second);
first = second;
second = tmp;
}
return second;
}
}原题链接:213 打家劫舍II

条件与上一题差不多,多了一个房屋成环的限制,那么只需要考虑两个可能性:
- 偷第0家,那么剩下可偷的房屋就从第2到第n - 2家里面选择;
- 不偷第0家,那么剩下的就从第1到第n - 1家里面选择。
剩下的房屋里的选择与上一题类似。最后得到两种可能性的最大值,返回即可。
class Solution {
public int rob(int[] nums) {
int n = nums.length;
return Math.max(nums[0] + rob(nums, 2, n - 1), rob(nums, 1, n));
}
private int rob(int[] nums, int start, int end) {
int first = 0, second = 0;
for (int i = start; i < end; ++i) {
int tmp = Math.max(second, first + nums[i]);
first = second;
second = tmp;
}
return second;
}
}原题链接:337 打家劫舍III
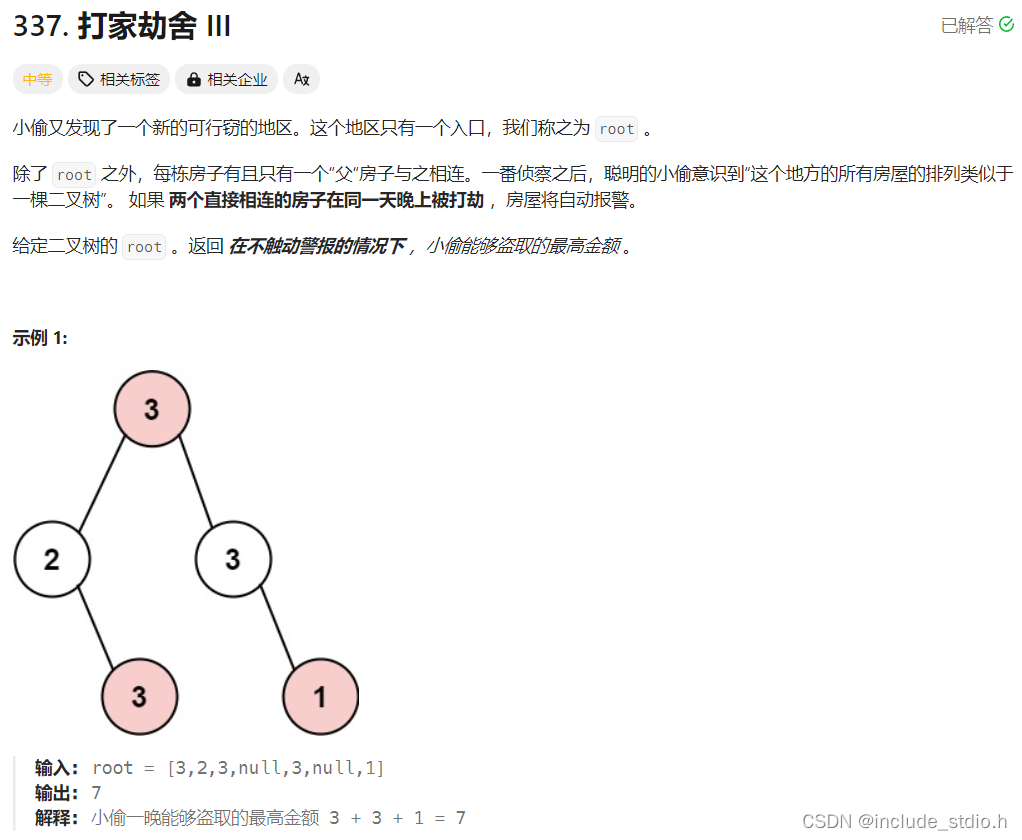
原分析在此处。这里涉及到递归和动态规划的结合。利用动规五部曲和递归三步逐步分析如下:
- 首先要考虑对树的遍历方式是前中后还是层序,这里需要后序遍历,往根节点的计算过程需要子节点的计算参与;
- 然后确定递归函数的参数和返回值。对于某一具体节点房屋,只有选择偷和不偷两种状态,因此该递归函数的返回值为长度为2的数组;同时,参数即为当前节点。其实,这里返回的数组即为dp数组,由于递归的存在,递归过程中系统会将前面每一层的参数保存起来。
- 再就是确定递归的终止条件。在遍历遇到空节点时,无论偷不偷,当前节点返回的值都将会是0,因此这里的递归终止条件即为:
if (cur == null) return new int[2];这里其实也就相当于对dp数组做了初始化。
-
紧接着需要确定的是动态规划过程中的遍历顺序。之前已经确定了要用后序遍历,因此遍历顺序为:通过递归遍历左子节点,获得偷或者不偷左子节点的金钱;通过递归遍历右子节点,获得偷或者不偷右子节点的金钱。
-
之后是确定单层递归的逻辑。如果选择偷当前节点,那么该节点的左右子节点就不能偷,于是有:val1 = cur.val + left[0] + right[0]; 如果选择不偷当前节点,那么该节点的左右子树就可以偷,具体偷不偷则要取决于最大化对该子节点的收益,即有:val2 = Math.max(left[0], left[1]) + Math.max(right[0], right[1])。这样即可得出当前节点的状态为:{val1, val2}。
以上即是分析过程,最后代码如下:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int rob(TreeNode root) {
int[] ans = robTree(root);
return Math.max(ans[0], ans[1]);
}
private int[] robTree(TreeNode root) {
if (root == null) return new int[2];
int[] left = robTree(root.left);
int[] right = robTree(root.right);
int val1 = root.val + left[0] + right[0];
int val2 = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
return new int[]{val2, val1};
}
}