文章目录
6.4 CNN和RNN的区别
6.5 RNNs与FNNs有什么区别
6.6 RNNs训练和传统ANN训练异同点
6.7 为什么RNN训练的时候Loss波动很大
6.8 标准RNN前向输出流程
6.9 BPTT算法推导
6.9 RNN中为什么会出现梯度消失
6.10 如何解决RNN中的梯度消失问题
6.4 CNN和RNN的区别
| 类别 | 特点描述 |
|---|---|
| 相同点 | 1、传统神经网络的扩展 2、前向计算产生结果,反向计算模型更新 3、每层神经网络横向可以多个神经元共存,纵向可以有多层神经网络连接 |
| 不同点 | 1、CNN空间扩展,神经元与特征卷积;RNN时间扩展,神经元与多个时间输出计算 2、RNN可以用于描述时间上连续状态的输出,有记忆功能,CNN用于静态输出 |
6.5 RNNs与FNNs有什么区别
1. 不同于传统的前馈神经网络(FNNs),RNNs引入了定向循环,能够处理输入之间前后关联问题。
2. RNNs可以记忆之前步骤的训练信息。
定向循环结构如下图所示:

6.6 RNNs训练和传统ANN训练异同点
相同点:
- RNNs与传统ANN都使用BP(Back Propagation)误差反向传播算法。
不同点:
- RNNs网络参数W,U,V是共享的(具体在本章6.2节中已介绍),而传统神经网络各层参数间没有直接联系。
- 对于RNNs,在使用梯度下降算法中,每一步的输出不仅依赖当前步的网络,还依赖于之前若干步的网络状态。
6.7 为什么RNN训练的时候Loss波动很大
由于RNN特有的memory会影响后期其他的RNN的特点,梯度时大时小,learning rate没法个性化的调整,导致RNN在train的过程中,Loss会震荡起伏,为理论解决RNN的这个问题,在训练的时候,可以设置临界值,当梯度大于某个临界值,直接截断,用这个临界值作为梯度的大小,防止大幅震荡。
6.8 标准RNN前向输出流程
以表示输入,
是隐层单元,
是输出,
为损失函数,
为训练集标签。
表示
时刻的状态,
是权值,同一类型的连接权值相同。以下图为例进行说明标准RNN的前向传播算法:
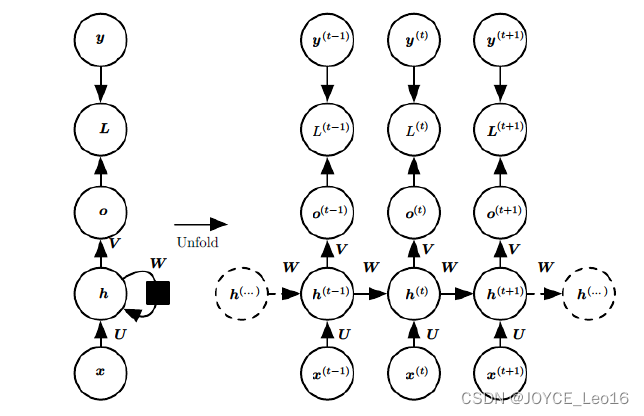
对于时刻,
,其中
为激活函数,一般会选择tanh函数,
为偏置。
时刻的输出为:
模型的预测输出为:
其中,为激活函数,通常RNN用于分类,故这里一般用softmax函数。
6.9 BPTT算法推导
BPTT(back-propagation through time)算法是常用的训练RNN的方法,其本质还是BP算法,只不过RNN处理时间序列数据,所以要基于时间反向传播,故叫随时间反向传播。BPTT的中心思想进而BP算法相同,沿着需要优化的参数的负梯度方向不断寻找更优的点直至收敛。
需要寻优的参数有三个,分别是U、V、W。与BP算法不同的是,其中W和U两个参数的寻优过程需要追溯之前的历史数据,参数V相对简单只需关注目前,那么我们就先来求解参数V的偏导数。
RNN的损失也是会随着时间累加的,所以不能只求时刻的偏导。
W和U的偏导的求解由于需要涉及历史数据,其偏导求起来相当复杂。为了简化推导过程,我们假设只有三个时刻,那么在第三个时刻对
,
对
的偏导数分别为:
可以观察到,在某个时刻的对或是
的偏导数,需要追溯这个时刻之前所有时刻的信息。根据上面两个式子得出
在
时刻对
和
偏导数的通式:
整体的偏导公式就是将其按时刻再一一加起来。
6.9 RNN中为什么会出现梯度消失
首先来看tanh函数的函数及导数图如下所示:

sigmoid函数的函数及导数图如下所示:

从上图观察可知,sigmoid函数的导数范围是(0,0.25],tanh函数的导数范围是(0,1],它们的导数最大都不大于1。
基于6.8章节中公式的推导,RNN的激活函数是嵌套在里面的,如果选择激活函数为tanh或sigmoid,把激活函数放进去,拿出中间累乘的那部分可得:
梯度消失现象:
基于上式,会发现累乘会导致激活函数导数的累乘,如果取tanh或sigmoid函数作为激活函数的话,那么必然是一堆小数在做乘法,结果就是越乘越小。随着时间序列的不断深入,小数的累乘就会导致梯度越来越小直到接近于0,这就是“梯度消失”现象。
实际使用中,会优先选择tanh函数,原因是tanh函数相对于sigmoid函数来说梯度较大,收敛速度更快且引起梯度消失更慢。
6.10 如何解决RNN中的梯度消失问题
上节描述的梯度消失是在无限的利用历史数据而造成,但是RNN的特点本来就是能利用历史数据获取更多的可利用信息,解决RNN中的梯度消失方法主要有:
- 选取更好的激活函数,如ReLU激活函数。ReLU函数的左侧导数为0,右侧导数恒为1,这就避免了“梯度消失”的发生。但恒为1的导数容易导致“梯度爆炸”,但设定合适的阈值可以解决这个问题。
- 加入BN层,其优点包括可加速收敛、控制过拟合,可以少用或不用Dropout和正则、降低网络对初始化权重不敏感,且能允许使用较大的学习率等。
- 改变传播结构,LSTM结构可以有效解决这个问题。