ES入门十一：正排索引和倒排索引

索引本质上就是一种加快检索数据的存储结构，就像书本的目录一下。

为了更好的理解正排索引和倒排索引，我们借由一个 **唐诗宋词比赛，**这个比赛一共有两个项目：

给定诗词名称，背诵整首
给诗词中几个词语，让你说出带这些词语的诗词。

不难想到，1比较简单，就是一个正向索引，2比较难，属于逆向索引

正排索引

如果想赢得第一个项目，我们怎么设计，我们可以把诗词名作为key，然后诗词内容作为value，然后放到hash中存储起来。像这种我们吧实体id到数据内容实体的关联关系的索引我们称之为正排索引

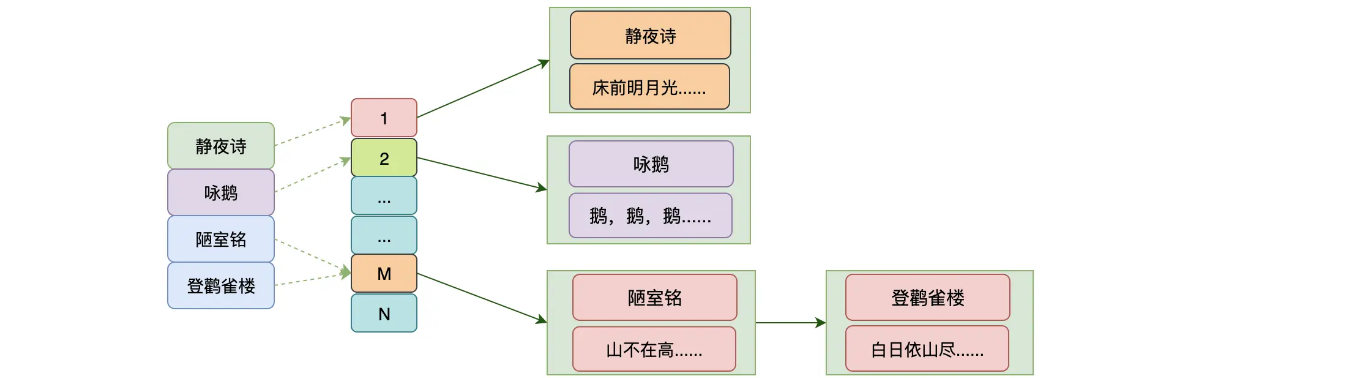
倒排索引

但是如果说我们想通过词语来找出哪些诗词中含有这些诗词，这个怎么做哪？不能用hash这种来存储了，这里就可以考虑倒排索引，

将所有诗词的内容进行分词
建立各个词语到诗词名称的索引

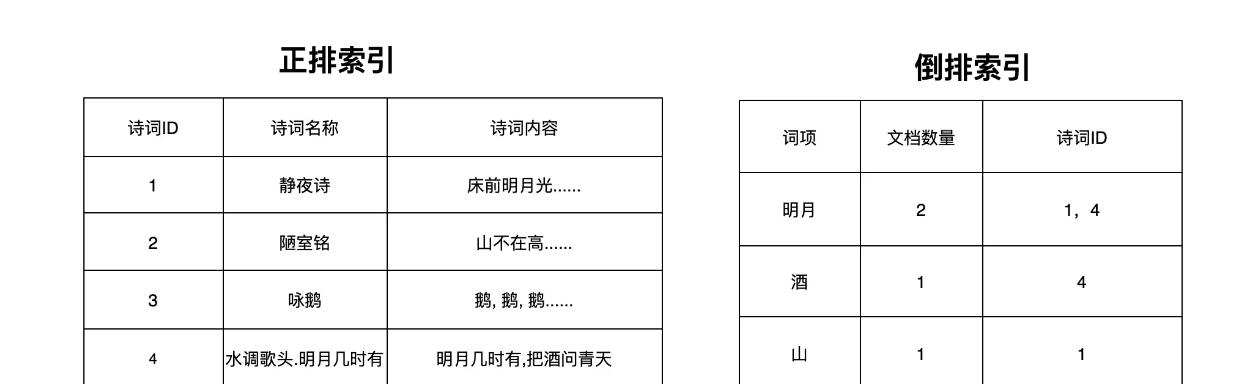
根据倒排索引，我们可以

获取诗词（词项）对应的文档id
如果有多个诗词（词项）也就会获取到多个文档id，然后做交集即可。
最后通过交集的文档id去文档里面找

用hash行不行

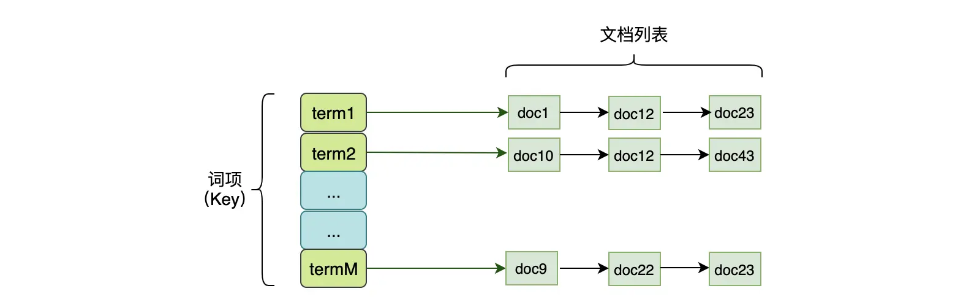
如上图，我们看起来用hash实现也是可以的，但是哪，如果数据量非常大，你想想诗词中取这个key得多少，更别说其他需求了。所以简单的使用hash是不行的，因为在存储海量数据的时候，系统将会面临下面这些问题：

分词形成的词项（term）可能是海量的，需要可以在内存和磁盘上高效存储
既然词项是海量的，那么如何快速找到对应的词项也是个问题
每个词项对应的文档可能非常多，也就是上图中的文档列表很长
在词项对应的文档多的情况下，多个文档列表做交集也是一个很大的问题

是不是感觉很难？
其实就是词项和文档列表的问题

Lucene的倒排索引的实现中，使用词项索引（Term Index）解决了问题1和问题2
Lucene使用Roaring Bitmaps、跳表等技术解决了问题3和问题4

倒排索引的原理

倒排索引的组成一共有3个部分：

Term Index
Term Dictionary
Posting List

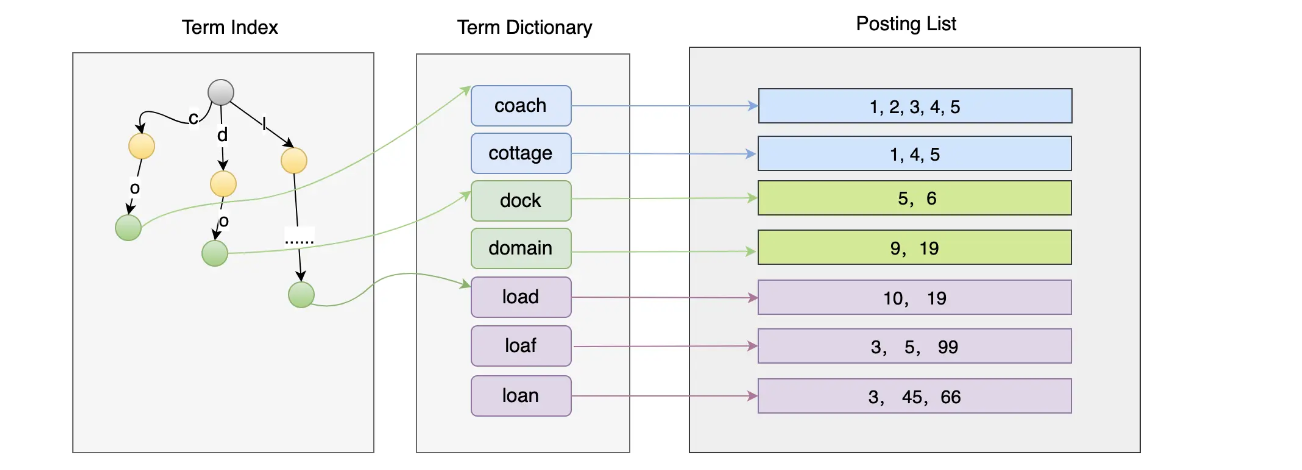
Term Dictionary放的是词项，如果词项越来越多查询肯定不行，所以就有了**Term Index，它是Term Dictionary的索引，最好设计得越小越好，这样缓存在内存中也没有压力。**Posting LIst保存了每个词项对应的文档Id列表

Segment

在了解 Term Index、Term Dictionary、Posting List 的具体实现前，我们先来看看 Segment、文档、Field、Term 与它们的关系。

默认情况下，ES每秒会把缓存中的数据写入到Segment，然后根据某些规则进行刷盘，并且合并这些Segment。所以Segment的数据一旦写入就不变了，采用不变形有2个好处：

更新对磁盘来说不友好
一个可变的数据有并发写的问题

逻辑上，一个Segment上会有多个文档，一个文档有多个字段。如下图中的Segment就有两个文档，文档1和文档2都有两个Field。这些字段的内容会被分词器形成多个Term，然后以块的形式保存到Term Dictionary中，并且系统会对Term Dictionary的内容做索引形成Term Index。在搜索的时候，通过

Term Index找到Block
之后进一步找到Tem对应的Posting List中的文档Id
然后计算出符合条件的文档Id列表

需要注意的是，Segment中的每个字段（Field）都会有自己的Term Index、Term Dictionary、Posting List结构，也就是说每个Field中的这些结构都是独立的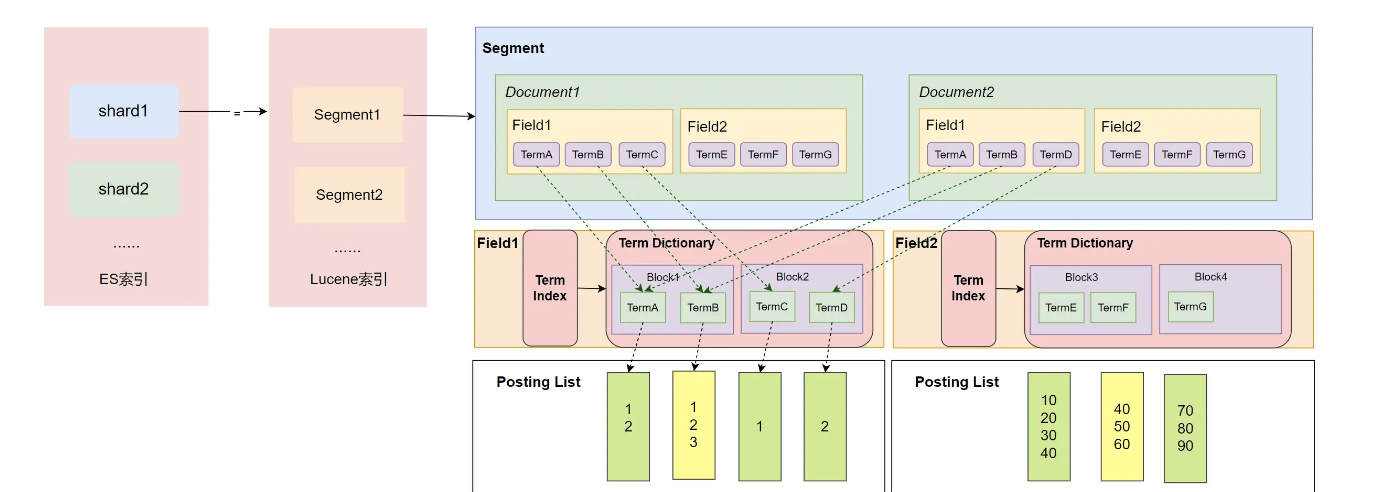

Term Index的实现

Term Index作为Term Dictionary的索引，其最好是资源消耗小，可以缓存在内存中，而且数据查找有较低的复杂度。在讨论Tem Index如何实现前，看下面这几个词语：

这两对词语分别有公共的前缀：co和do。如果我们把Term Dictionary中的Term排序后按公共前缀抽取出来按块存储，而Term Index只使用公共前缀做索引，那本身要存储coach、cottage两个字符串的索引，现在只需要存储co一个就行了。这样的话，拥有同一个公共前缀的Term越多，实际上就是越省空间，并且这种设计在查找的时候复杂度是前缀公共的长度：0（length（prefix））

但是这样的索引也有缺点，它只能找到公共前缀所在的块的地址，所以它既无法判断这个Term是否存在，也不知道这个Temr保存在Term Dictionary（.tim）文件具体在什么位置上。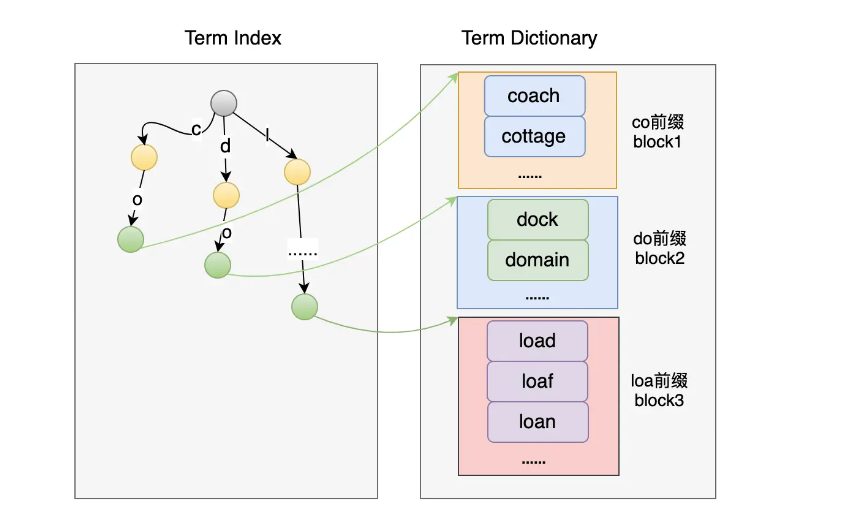

如上图，对于在每个块中如何快速查找到对应的Term，我们可以使用二分法来搜索，因为Block中的数据是有序的。但机智的你是不是也发现可以优化的地方？因为前缀在Term Index中保存了，那么Block中就不要为每个Term在保存对应的前缀了，所以Block中保存的每个Term都可以省略掉前缀了。比如，co 前缀的 block1 中保存的内容为 ach、ttage 即可。

**对于前缀索引的实现，业界使用了FST 算法来解决。**FST（Finite State Transducers）是一种 FSM（Finite State Machines，有限状态机），并且有着类似于 Trie 树的结构。下面来简单了解一下 FST。

FST有以下特点：

通过对Term Dictionary数据的前缀复用，压缩了存储空间
高效的查询性能，O(len(prefix))的复杂度；
构建后不可变。（事实上，倒排索引一旦生成就不可变了。）

下图是一个简单的FST图。从图中可以看出，一条边有两个元素label和out，其中label为key的元素，例如cat这个key 就有 c、a、t 这三个元素，out为此边的值value。小圆圈为FST的一个节点，节点分为两类-普通节点和Final节点，图中灰黑色的为Final节点，Final节点中还有Finalout，代表 Final 节点的值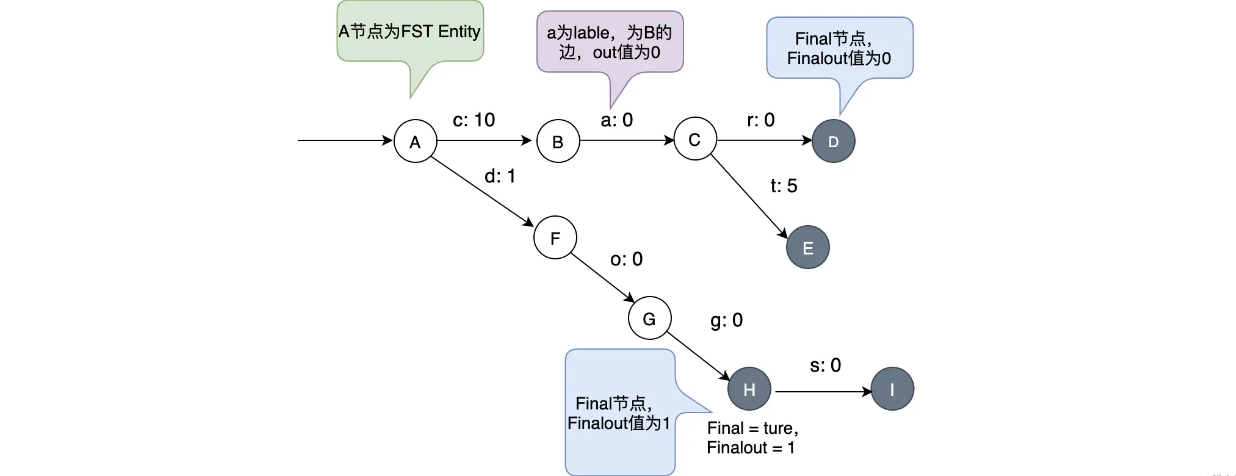

当访问cat的时候，读取 c、a、t 的值作和，再加上 Final 节点的 Finalout 值即可：10 + 0 + 5 + 0 = 15；当访问 dog 的时候，读取 d、o、g 的值即可，但是由于 g 为 Final，所以需要加上 g 的 Finalout：1 + 0 + 0 + 1 = 2。

简单的可以理解为这个：不需要看上面ABC这些大的节点，直接看边，cat就是c+a+t，另外看这个t是不是final节点，如果dog的话还需要加上g为final out =1

Term Dictionary的实现

在倒排索引组成的3个部分中，Term dictionary保存了Term和Posting List的关系，存储了Term相关的信息，比如记录该Term的文档数量、Term在Segment中出现的频率，还保存了指向Posting List的指针（文档列表的id的位置、词频位置等），

如下图，在对Term Dictionary 做索引的时候，先将所有的Term进行排序，然后将Term Dictionary中有共同前缀的Term抽取出来进行存储，再对共同前缀索引，最后通过索引就可以找到公共前缀对应的块在Term Dictionary文件中的偏移地址。

由于每个块中都有共同前缀，所以不需要再保存每个Term的全部内容，只需要保存其后缀即可，而且这些后缀都是排好序的。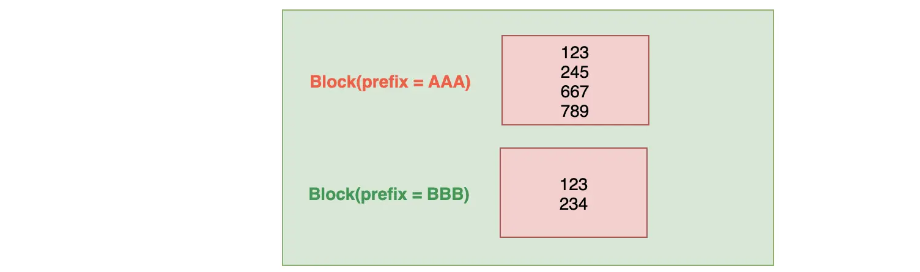

至此，我们就可以通过Term Index 和 Term Dictionary 快速判断一个 Term 是否存在，并且存在的时候还可以快速找到对应的 Posting List 信息

Posting List的实现

上面的Posting List并不是只是包含文档ID，其实Posting List包含的信息比较多，如文档Id、词频、位置等等。Lucence把这些数据分成三个文件进行存储：

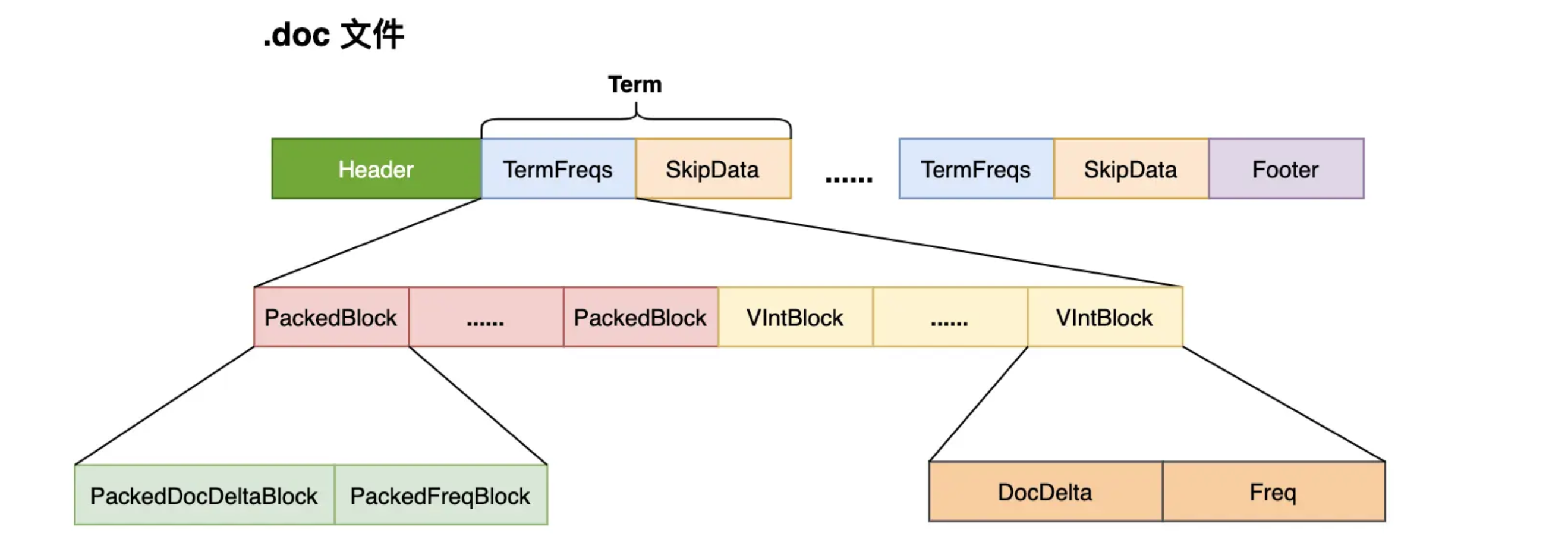
.doc文件，记录了文档Id信息和Term的词频，还记录了跳跃表信息，用来加速文档Id的查询；还记录了Term在pos和pay文件中的位置，有助于进行快速读取
.pay文件，记录了Payload信息和Term在doc中的偏移信息；
.pos文件，记录了Term在doc中的位置信息

因为倒排索引的主要目的就是找到文档id，所以下面讨论Posting List的时候我们就关注文档Id的信息，其他的就忽略了。前面提到过，Posting List主要面临2个问题：

如果节省存储
如何快速做交集

要节省存储，可以对数据进行压缩存储；至于如何做交集，业界应用的得比较多的是跳表、Roaring Bitmaps等技术。下面我们就针对这两个问题以及对应的方法分别讲解一下：

节省存储：整形压缩

不知道你有没有留意过，其实int类型或者long类型是可以进行压缩的。我们可以根据需要处理的数据的取值范围，选择占用更小字节数的数据类型来存储原数据，例如下面的Int数组：

# Int数组
[8, 12, 100, 140]

# 各个元素与其二进制表示
8 -> 00001000
12 -> 00001100
100 -> 01100100
140 -> 10001100

这个Int数组，如果每个数据都需要用4个字节来保存的话，需要16个字节。但你会发现，数组中最大的数140只需要用8位（一个字节）就可以表示了。这样一来，原来需要16个字节的数据只需要4个字节就可以表示了。

整数压缩基本就是这个思路了，当然还有其他玩法（下面介绍的VintBlock），但核心的思想都是：用最少的位数来表示原数据，并且兼顾数据读取效率。Lucene在Posting List中使用了2种编码格式来对整形类型的数据进行压缩- PackedBlock和VinBlock，并且在对整数进行压缩的基础上，还会对文档Id使用差值存储的方式来对数据进一步的压缩处理。

PackedBlock

在Lucene中，每当处理完128个包含某个Term的文档是，就会将这个文档Id和词频使用的PackedInts进行压缩存储，生成一个PackedBlock。PackedBlock中使用两个数组，一个是存储文档id的，一个是存储词频的。所以PackedBlock是存储固定长度的整形数组的结构，且数组的长度为128.

下面简单介绍一下PackedInts的实现，PackedInts会将Int[] 压缩打包成一个Block，其压缩方式是把数组中最大的那个数占用的有效位数作为标准，然后各个元素打包的数组中，每个元素都按这个有效位数来算，例如下面数组：

# Int数组
[8, 12, 100, 120]

# 各个元素与其二进制表示
8 -> 0001000
12 -> 0001100
100 -> 1100100
120 -> 1111000

最大数120的有效位数是7，所以数组中所有数据都可以使用7位来表示。假设这个数组有128个元素，且最大位120，那么这个压缩后的数组就如以下：

最终这个数组占用的位数位7bit * 128 = 896bit =112字节（这里没有算len占用的空间，但是不要忽略len也是要花费空间存储的），这比起原数据128 * 4字节=512字节确实节省了不少

PackedBlock只能存储固定长度的数组数据，如果一个Segment的文档数不是128的整数倍，那该怎么办那？这时可以使用VintBlock来进行存储

VintBlock

VintBlock通过使用变长整形编码方式来进行压缩，所以其可以存储复合的数据类型，不需要想PackedInts那样规定数据元素是多少位的。VintBlock采用Vint来对Int类型进行压缩，Vint采用可变长的字节来表示一个整数，每个字节只使用第1位到第7位来存储数据，第8位用来作为是否需要读取下一个字节的标记

如上图，本身Int 200需要4个字节，使用Vint只需要2个字节存储即可

使用PackedBlock与VintBlock来解析.doc文件

Lucene在处理文档的时候，每处理 128 篇文档就会将其对应的文档 ID 数组（docDeltaBuffer）和词频（TermFreq）数组（freqBuffer）处理为两个 Block：并且使用 PackedInts 类对数据进行压缩存储，生成一个 PackedBlock。而把最后不足 128 篇文档的数据采用 VIntBlock 来存储（如果有 131 个文档，会生成一个 PackedBlock 和 3 个 VIntBlock）。并且在生成 PackedBlock 的时候，会生成跳表（SkipData），使得在读取数据时可以快速跳到指定的 PackedBlock。
下图为你整理了处理 .doc 文件的数据结构，以加深你对 Posting List 的理解。

使用文档Id差值存储来节省空间

整数的压缩可以使当个数值占用的空间得以减少，但数与数之间还存在着微妙的关系，两个正整数的差一定会比它们种最大的那一个要小
利用这个特性，我们可以使需要压缩的整数变成最小的数，从而进一步压缩空间。因为存储文档Id的数组是有序的（需要注意的是，词频是无序的，无法使用下面的处理方式），所以在保存文档ID的时候，docDeltaBuffer 中存的不是文档的 ID，而是与上一个文档 ID 的差值，这样做可以进一步压缩存储空间！

ids = [1, 4, 6, 9, 14, 17, 21, 25]

如上面给定的数组 ids，如果用 PackedInts 的方式来对数据进行压缩的话，那么25（0001 1001）最少需要用 5 bit 来存储，所以整个数组需要 5 * 8 = 40 bit 来存储。如果数组中存储的是文档 ID 的差值，那么这个差值数组如下：

dtIds = [1, 3, 2, 3, 5, 3, 4, 4]

dtIds 数组中最大值为 5（0000 0101），其最少需要 3 bit 来表示，那么整个数组只需要 3 * 8 = 24 bit，相对于原来需要 40 bit 来存储数据，差值存储的方式可以有效降低存储的空间。探其究竟，其实是两个正整数间的差值会比它们间最大的那个要小，那么需要的有效位数就可能会减少了。
其实综合了上面所有的流程，无非就是文档 ID 使用增量编码，数据分块存储、数据按需分配存储空间，而这整个过程叫做 FOR（Frame Of Reference） 。

2.2.4.2 文档Id列表的交集求解

如果你需要检索朝代是唐代、诗人姓李、诗名中包含“明月”的诗，这时候系统会返回 3 条包含对应文档 ID 的列表，如下图：

如果直接循环3个数组求交集，并不是很高效，下面对其进行优化。

位图

如果我们将列表的数据改造成位图会如何？假设有两个posting list A、B和它们生成的位图如下：

A = [2, 3, 5] => BitmapA = [0, 0, 1, 1, 0, 1]
B = [1, 2, 5] => BitmapB = [0, 1, 1, 0, 0, 1]

BitmapA AND BitmapB = [0, 0, 1, 0, 0, 1]

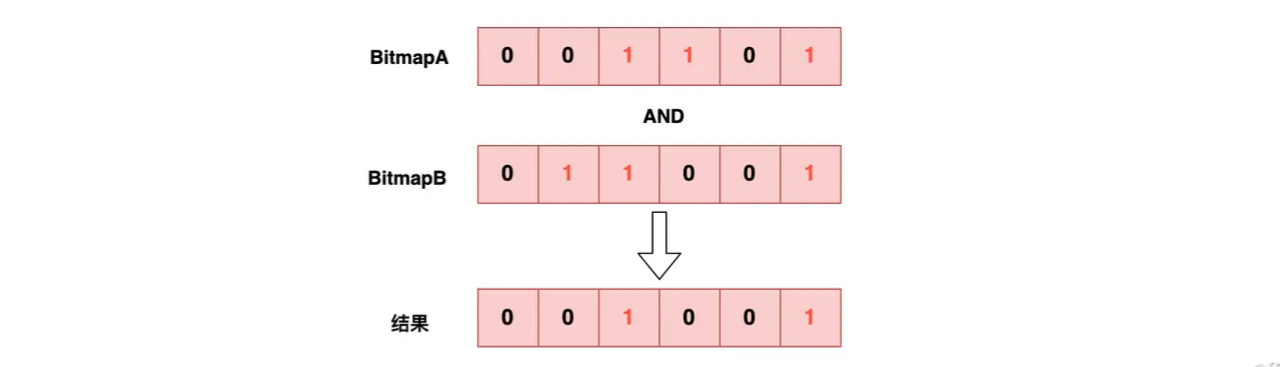
生成位图的方式其实很简单：Bitmap[A[i]] = 1，其他为 0 即可。这样我们可以将 A、B 两个位图对应的位置直接做 AND 位运算，由于位图的长度是固定的，所以两个位图的 AND 运算的复杂度也是固定的，并且由于 CPU 执行位运算效率非常高，所以在位图不是特别大的情况下，使用位图求解交集是非常高效的。

但是位图位图也有其致命的缺点，总结下来有这几点：

位图可能会消耗大量的空间。即使位图只需要1bit就可以表示相对应的元素是否存在，但是如果一个列表的有一个元素特别大，例如数组 [1, 65535]，则需要 65535 bit 来表示。如果用 int32 类型的数组来表示的话，一个位图就需要 512M（2^32 bit = 2^29 Byte = 512M），如果有 N 个这样的列表，需要的存储空间为 N * 512M，这个空间开销是非常可怕的！
位图只适合数据稠密的场景
位图只适合存储简单整形类型的数据，对于复杂的对象类型无法处理，或者说复杂的类型本身就无法在CPU上直接使用AND这样的操作符

业界为了解决位图空间消耗大的问题，会使用一种压缩位图技术，也就是Roading Bitmap来代替简单的位图。Roadring Bitmap在业界应用广泛，下面来看看Roaring Bitmap的实现

Roaring Bitmaps

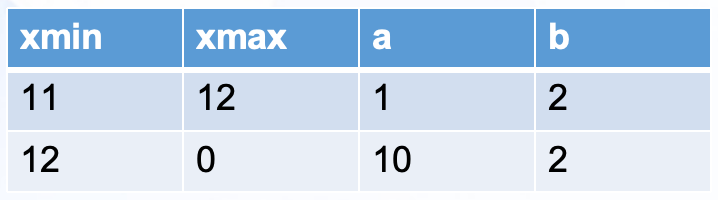
它会把一个 32 位的整数分成两个部分：高 16 位和低 16 位。然后将高 16 位作为一个数值存储到有序数组里，这个数组的每一个元素都是一个块。而低 16 位则存储到 2^16 的位图中去，将对应的位置设置为 1。这样每个块对应一个位图，如下图：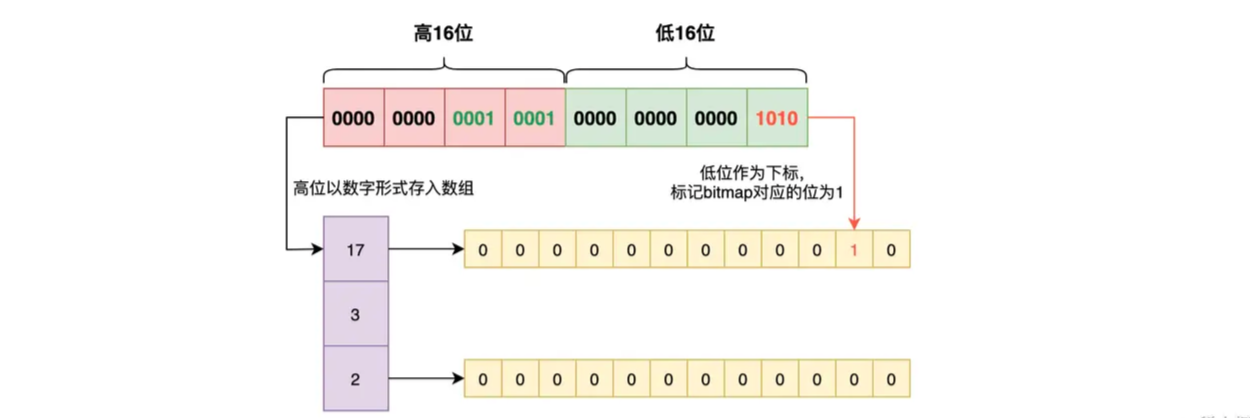

Roaring Bitmaps 通过拆分数据，形成按需分配的有序数组 + Bitmaps 的形式来节省空间。其中一个 Bitmaps 最多 2^16 个 bit，共消耗 8K。而由于每个块中存的是整数，每个数需要 2 个字节来存储即可，这样的整数共有 2^16 个，所以有序数组最多消耗 2 Byte * 2^16 = 128K 的存储空间。由于存储块的有序数组是按需分配的，所以 Roaring Bitmaps 的存储空间由数据量来决定，而 Bitmaps 的存储空间则是由最大的数来决定。举个例子就是，数组[0, 2^32 - 1]，使用 Bitmaps 的话需要 512M 来存储，而 Roaring Bitmaps只需要 2 * (2 Byte + 8K)。
由于 Roaring Bitmaps 由有序数组加上 Bitmaps 构成，所以要确认一个数是否在 Roaring Bitmaps 中，需要通过两次查询才能得到结果。先以高 16 位在有序数组中进行二分查找，其复杂度为 O(log n)；如果存在，则再拿低 16 位在对应的 Bitmaps 中查找，判断对应的位置是否为 1 即可，此时复杂度为 O(1)。所以，Roaring Bitmaps 可以做到节省空间的同时，还有着高效的检索能力。
但是机智的你不知道有没有看出来，如果每个块的 Bitmaps 一直消耗 8K 的存储是不是超级浪费？如果这一个块中的数据很少，或者很稀疏，那还不如把 Bitmaps 做成数组呢。那到底用数组还是用 Bitmaps，阈值在哪里呢？当数据量达到 4096 的时候，我们发现 4096 * 16 bit(2 Byte) = 8K，所以当一个块的数据量小于 4096 的时候，可以使用 short 类型的有序数组存储数据，并且使用变长数组进一步节省空间。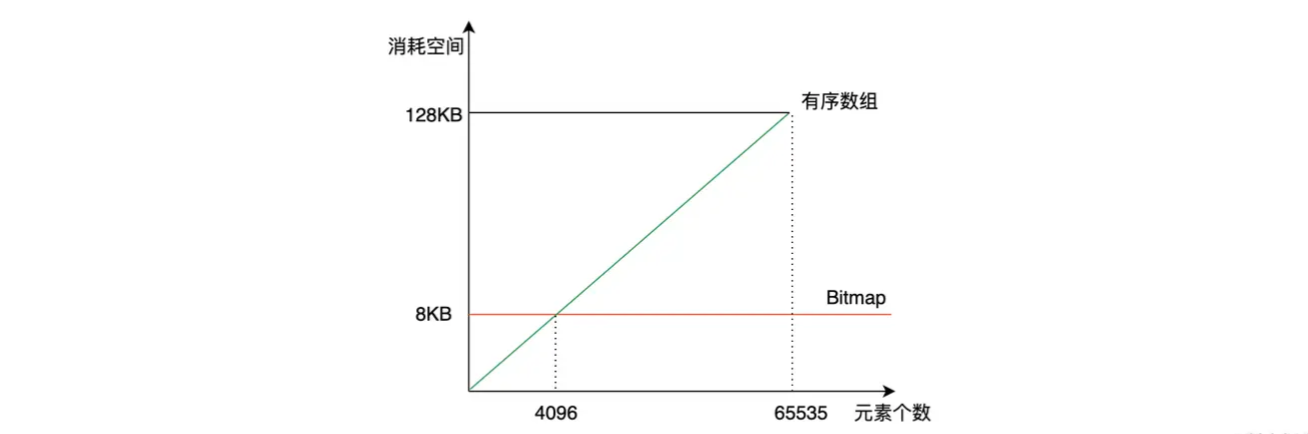

业界除了使用 Roaring Bitmaps 来求交集外，还使用了跳表。

使用跳表加速多个列表交集的求解

跳表是一种有序的数据结构，它通过在每个节点中维持多个指向其他节点的索引，从而达到快速访问的目的。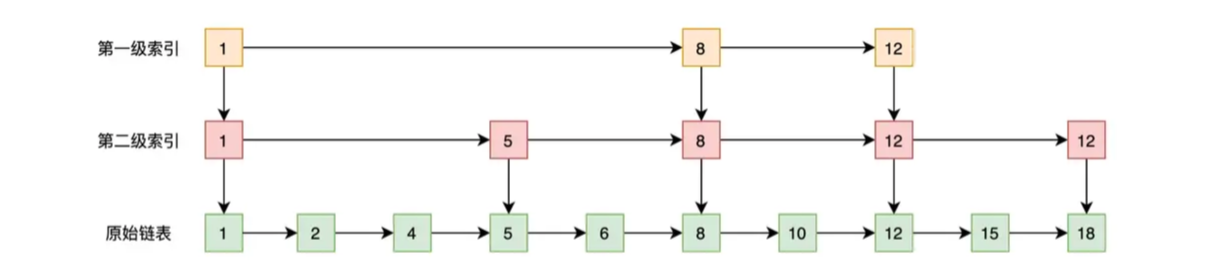

如上图，有序链表不能像有序数组那样使用二分法进行快速访问，但可以对有序链表维护一层或者多层索引使其快速访问。
在求解两个有序列表 A 和 B 的交集时，可以使用归并排序的方法来遍历两个列表，将复杂度从 O(M * N) 降低到 O(M + N)，这里的 M、N 分别为这两个列表的长度。
链表归并求交集的过程可以总结为以下三个步骤。

第一步：将指针 p1 和 p2 分别指向列表 A 和 B 的开头。
第二部：比较 p1 和 p2 指向的数据，会出现 3 种情况，如果内容相等，说明是公共元素，需要加入到结果集中；如果 p1 的内容小于 p2 的内容，p1 向后移；如果 p1 的内容大于 p2 的内容，p2 向后移。总结起来就是，谁小谁就往前走，相等就一起往前走，直到有一方结束！
第三步：重复第二步，直到 p1 或者 p2 到达链表尾为止。

这里我们再结合以下示意图和例子来加深一下对归并流程的理解。指针 p1 和 p2 的原位置如下图所示，下面我们就来看看它们是怎么移动的。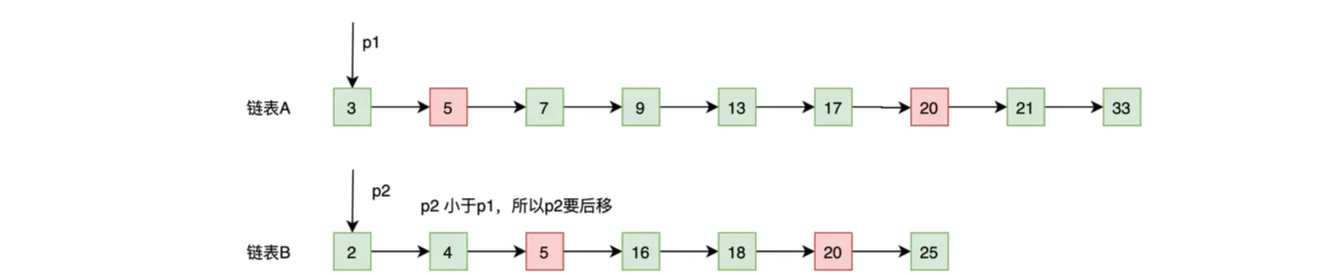

p2 的内容小于 p1 的内容（2 < 3），基于谁小谁就往前走的原则，所以 p2 往后移动一位，移动后的结果如下图：

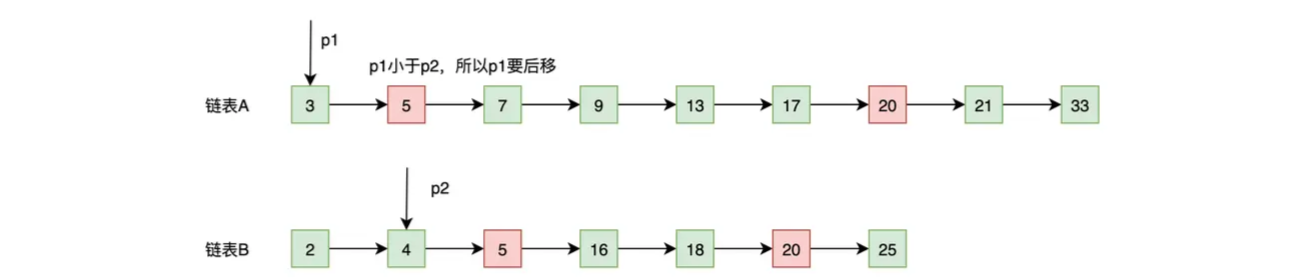
p1 的内容小于 p2 的内容（3 < 4），基于谁小谁就往后走的原则，所以 p1 往后移动一位，移动后的结果如下图：

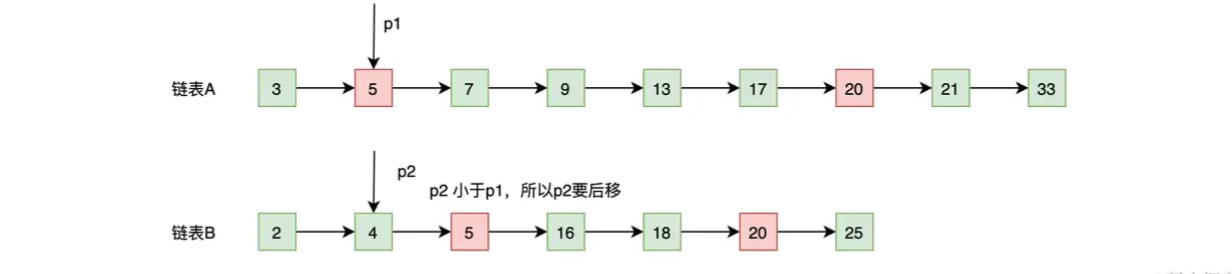
p2 的内容小于 p1 的内容（4 < 5），基于谁小谁就往后走的原则，所以 p2 往后移动一位，移动后的结果如下图：

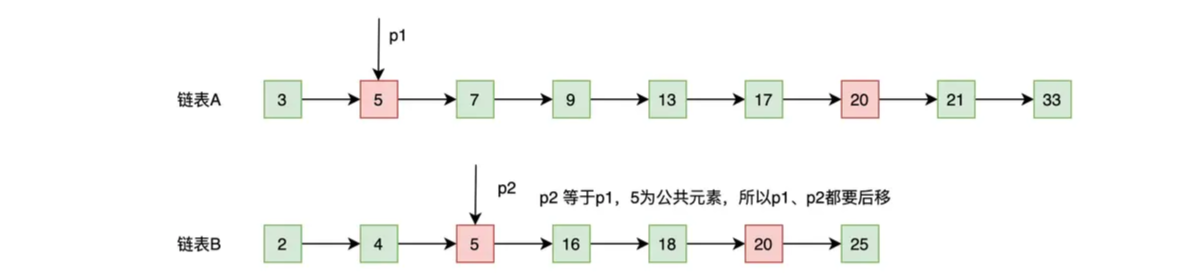
p2 的内容等于 p1 的内容（5 = 5），所以 5 为公共元素，需要记录下来，并且基于相等就一起往后走的原则，所以 p2 和 p1 都往后移动一位，移动后的结果如下图：

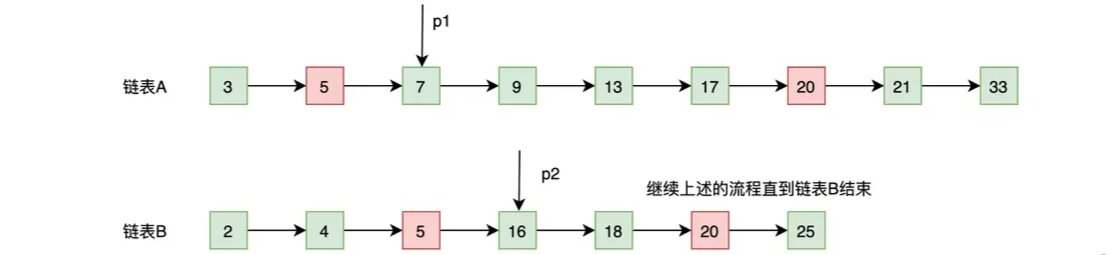
就这样，一直继续上述的流程直到链表B结束

归并排序的方式可以降低链表求交集的复杂度，但上述的算分还用优化的的地方。从下图中可以看出，此时 p1 要从 10 开始找直到多次才能找到 1000 这个大于或者等于 p2 的元素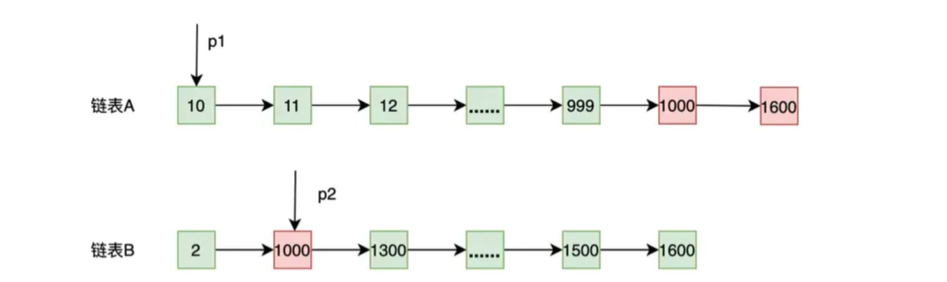

要优化这个问题，可以使用前面介绍的跳表，给链表做索引。下图中，p1 使用跳表索引经过比较少的次数就可以找到 1000 了。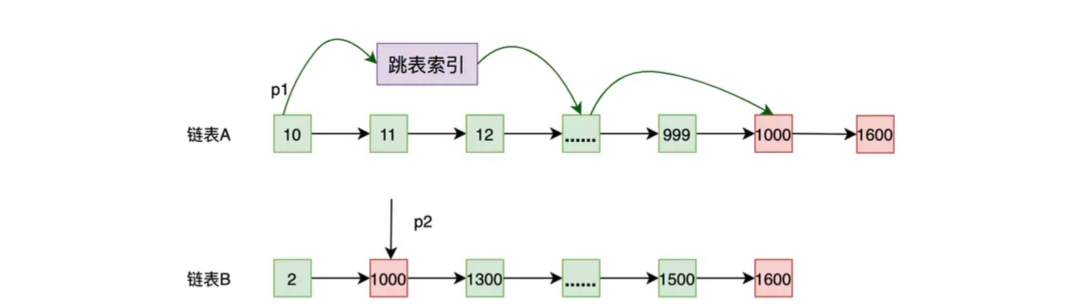

那既然链表 A 和 B 都有跳表索引的结构，那在链表 B 中查找数据也同样可以使用跳表索引的结构进行加速。如下图，当 p1 的值大于链表 B 当前值时，用 p1 的值当作 key，在链表 B 中使用二分查找，这样 p2 就可以使用跳表索引快速往前跳了。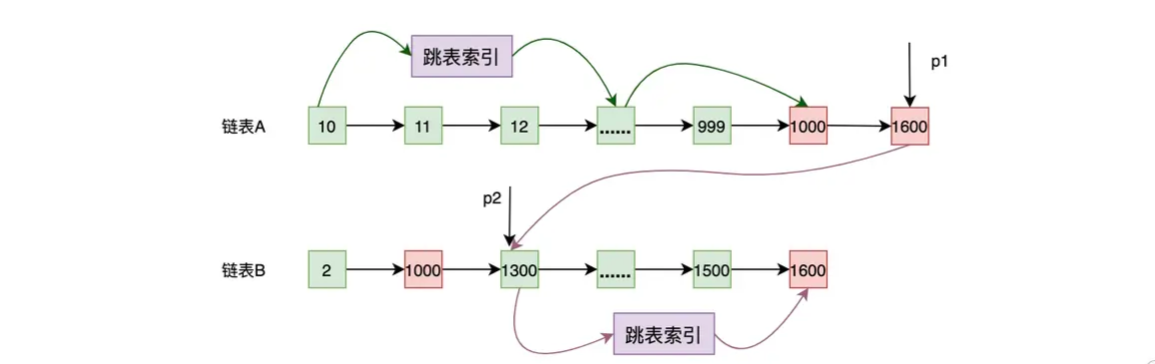

这种二分查找法可以总结为：谁当前值大，就用其作为 key 到其他列表中做二分查找。但是，需要说明的是，虽然使用跳表索引可以降低查询的复杂度，但是跳表索引是要消耗空间的，并且在构建跳表的时候，也需要消耗额外的时间！

总结

ES 中的倒排索引主要分为 3 个部分：Term Index、Term Dictionary 和 Posting List。

Term Index 是 Term Dictionary 的索引，使用它可以快速判断一个 Term 是否存在，并且可以找到这个 Term 在 Term Dictionary 存储的块地址。Term Index 使用了 FST 来实现，其有着小巧且复杂度低的特点。
而 Term Dictionary 是存储 Term 信息的地方，其内容包括 Term、包含该 Term 的文档的数量、Term 在整个 Segment 中出现的频率等。
我们还学习了 Posting List 的实现，了解了 Lucene 使用 PackedBlock 和 VIntBlock 对整数进行压缩的思路，也介绍了业界使用 Roaring Bitmaps 和跳表来解决列表求交集的方案。