---

前言

在计算机科学与算法领域中，二叉树作为一种基础且重要的数据结构，以其独特的组织方式和丰富的特性，广泛应用于诸多实际问题的解决方案。尤其在信息学奥林匹克竞赛（NOI）等高级别编程竞赛中，深入理解和熟练掌握二叉树的相关知识，是提升解题能力和应对复杂问题的关键一环。本篇文章旨在系统地阐述二叉树的定义、分类以及其基本性质，为读者搭建起扎实的理论基础，并通过实例解析与练习题，加深对二叉树特性的直观感知与运用能力。

学习路线：C++从入门到NOI学习路线

学习大纲：C++全国青少年信息学奥林匹克竞赛（NOI）入门级-大纲

---

一、二叉树的定义

在了解二叉树之前，我们先简单复习关于树的内容。

1. 树的定义

树（Tree）是由n（≥0）个节点的有限集。n=0时称为空树。在任意非空树中：

1. 有且仅有一个被称为根（Root）的节点，根节点没有前驱；
2. 树中的每个节点可以有零个或多个子节点；
3. 如果节点A是节点B的子节点，则节点B称为节点A的父节点；
4. 除了根节点外，每个节点有且仅有一个父节点；
5. 任意两个节点之间存在唯一的路径。

那么什么是二叉树呢？树是一种特殊的图，而二叉树是树的一种特殊形式。

比如我们把图比喻成灵长类。

那么树就是其中的一个分支，例如人猿总科。

二叉树又是树的一个分支。

它们之前的关系也可以用树来表示，如下所示：

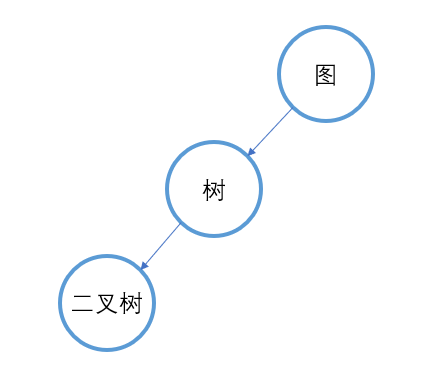
2. 二叉树的定义

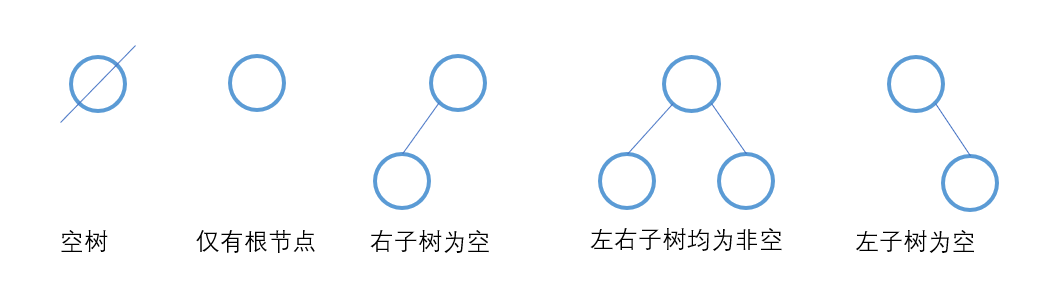
二叉树是n(n≥0)个结点的有限集合，这个集合或是空集，或是由一个根结点以及两棵互不相交的、被称为根的左子树和右子树所组成;左子树和右子树分别又是一棵二叉树。二叉树的特点:每个结点至多只有两棵子树，且二叉树的子树有左右之分，其次序不能任意颠倒。

二、满二叉树、完全二叉树和非完全二叉树

那什么是满二叉树、完全二叉树和非完全二叉树呢？它们和二叉树之间又有什么关系呢？

二叉树是最基础的二叉树类型，结构灵活多变；满二叉树是一种高度规则化的二叉树，所有节点都有两个子节点；完全二叉树在结构上接近满二叉树，但在最后一层允许部分节点缺失且保持左对齐，这种特性使得完全二叉树能够高效地用数组存储并应用于多种算法和数据结构中，而非完全二叉树是指任何不满足完全二叉树定义的二叉树。

具体关于满二叉树、完全二叉树和非完全二叉树的介绍可以看下面。

它们之前的关系也可以用树来表示，如下所示：

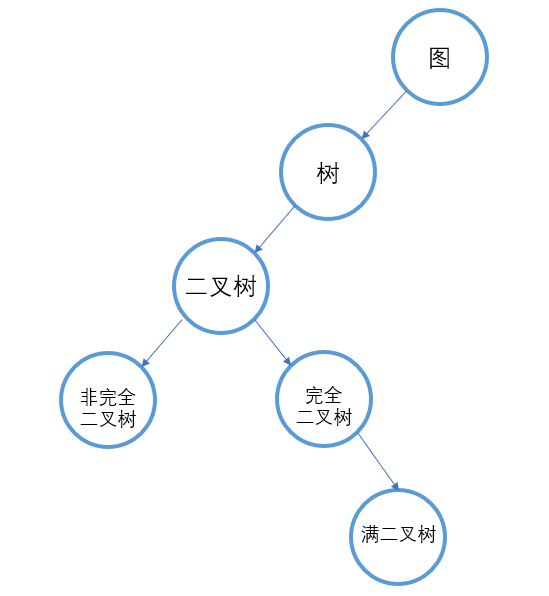
我们首先从最简单得满二叉树讲起。

1.满二叉树

满二叉树是二叉树的一个特殊类型。它的特点是，除了第一层外，每一层的节点都有两个子节点。也就是说，如果一个满二叉树的深度为K，那么它的节点总数就是(2^k) - 1。满二叉树是一种形态非常规则的树，其节点数是一系列固定的数。

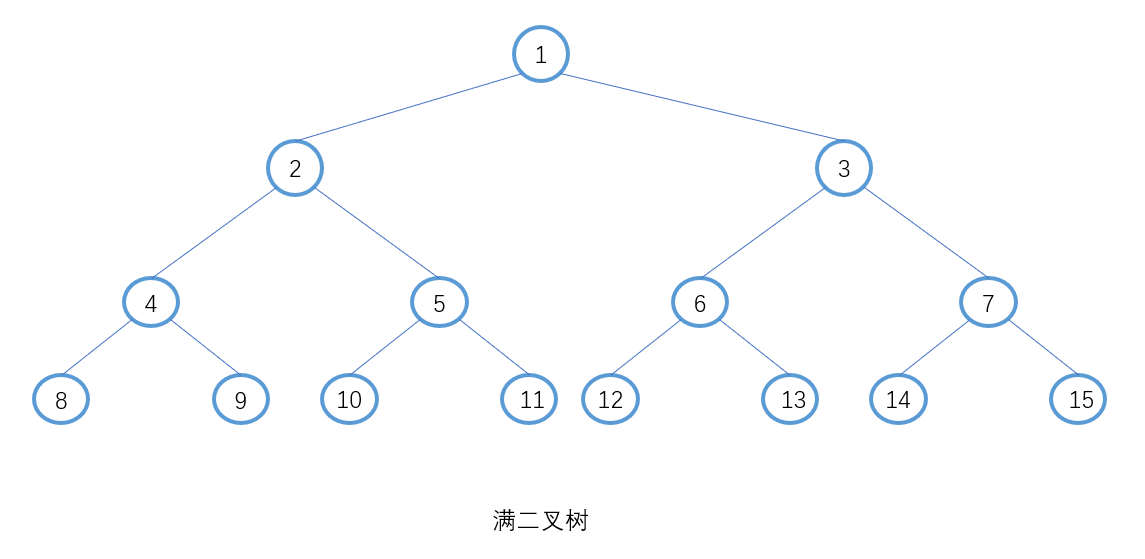
满二叉树是完全二叉树的一种特殊情况。换句话说，满二叉树必定是完全二叉树，但完全二叉树并不一定是满二叉树。

那什么是完全二叉树？

2.完全二叉树

完全二叉树是另一种特殊的二叉树，除了可能的最后一层外，每一层的节点数都达到最大（即完全填满），并且最后一层的所有节点都尽可能地靠左排列（即从左到右填充）。换句话说，对于完全二叉树，除了最后一个层级可能未填满外，其他层级都是满的，并且最后一个层级的叶子节点都集中在左侧。

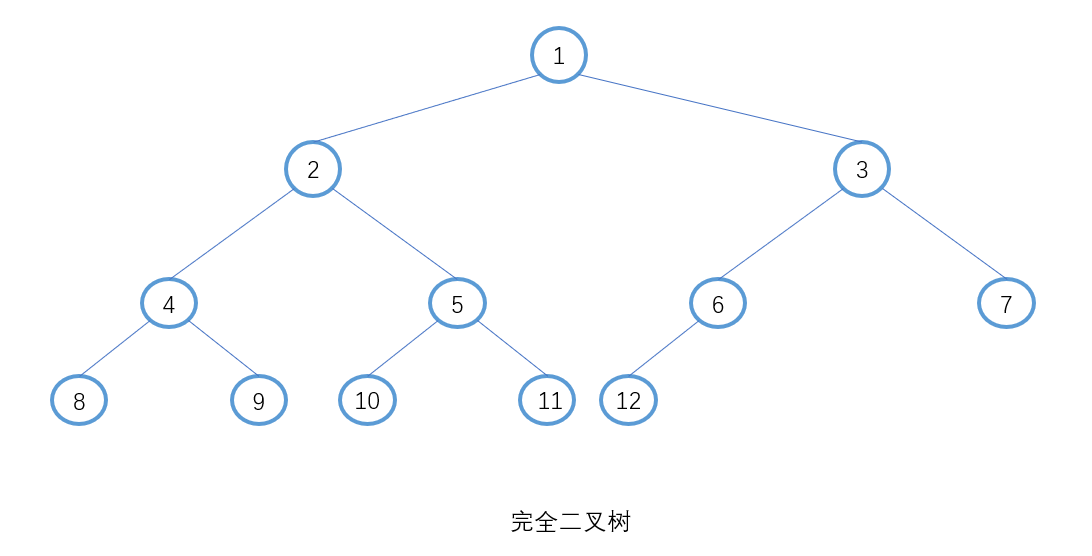
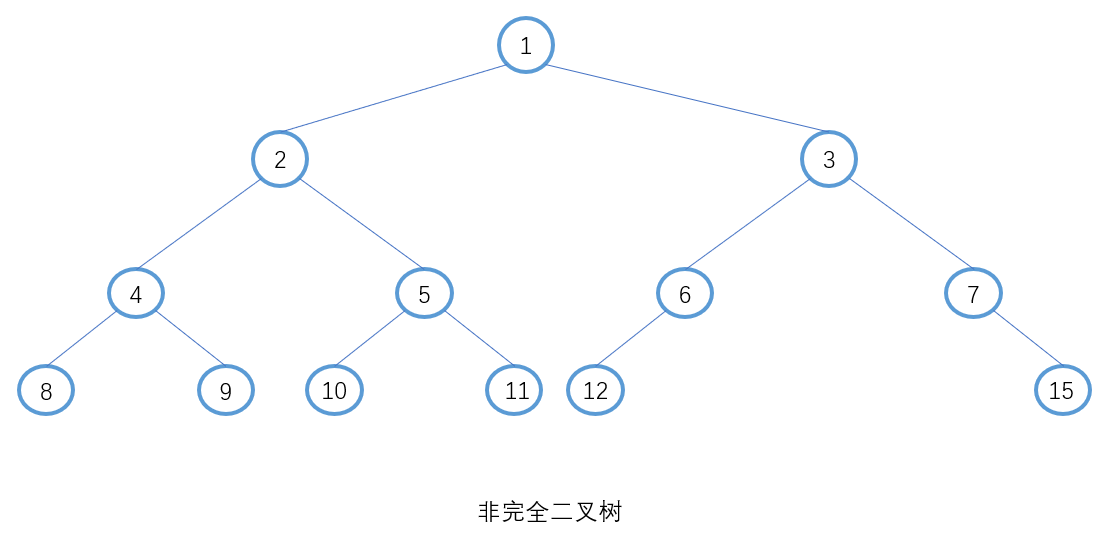
3.非完全二叉树

非完全二叉树是指任何不满足完全二叉树定义的二叉树。具体来说，非完全二叉树至少存在以下一种情况：

1. 除了最后一层外，至少有一层的节点数少于该层的最大可能数（即未填满）。
2. 即使最后一层节点数达到最大，但存在某个中间层节点数未达到该层最大可能数。
3. 最后一层的节点未按照从左到右的顺序排列，即使该层节点数达到了最大。

换言之，只要二叉树不符合完全二叉树的两个条件（所有非最后一层满节点，最后一层左对齐），它就被认为是非完全二叉树。非完全二叉树的形态可以非常多样，包括但不限于：

1. 中间层有节点缺失。
2. 最后一层节点数量未达到最大，且分布不均匀（未左对齐）。
3. 最后一层虽填满节点，但前面有中间层未填满。

三、二叉树的性质

接下来我们需要了解关于二叉树的五条性质。

这些性质有助于我们更好地理解和分析二叉树的结构特征、节点数量关系以及节点间父子关系。

性质1: 在二叉树的第i层上至多有2^(i-1)个结点 (i≥1)。

二叉树的每一层节点数最多按照指数级增长。第一层（根节点所在层）有1个节点（2^0=1 ） ，第二层最多有2个节点（2^1=2 ），第三层最多有4个节点（2^2=4 ），以此类推。每一层节点数是前一层节点数的两倍。这个性质源于二叉树每个节点最多有两个子节点的特性。

性质2: 深度为h的二叉树至多有2^h - 1个结点 (h≥1)。

深度为h的二叉树意味着它有h层。根据性质1，我们知道第i层最多有2^i-1个节点。将这一规律应用到每一层，累加所有层的节点数，得到的总节点数上限就是：

∑(2^i-1) for i = 1 to h = (2^1 - 1) + (2^2 - 1) + ... + (2^h - 1) = 2^h - 1

即深度为h的二叉树最多有2^h -1个节点。

性质3: 对任何一棵二叉树，如果其叶结点数n0，度为2的结点数为n2，则一定满足: n0 = n2 + 1。

这个性质揭示了二叉树中叶节点（度为0的节点，没有子节点）与度为2的节点（有两个子节点）之间存在的固定数量关系。为了理解这个关系，我们可以考虑以下两个操作：

1. 增加一个度为2的节点：当我们在二叉树中添加一个度为2的新节点时，这个新节点会带来两个新的子节点。这两个子节点中，必定有一个是新的叶节点（因为它没有子节点），另一个则会使得原有的一个叶节点的度增加到1（因为它成为了新节点的一个子节点）。因此，每增加一个度为2的节点，叶节点总数会增加1。

2. 减少一个叶节点： 反过来，如果我们想减少一个叶节点，必须从二叉树中去掉一个叶节点及其所有祖先（直至找到一个度为2的节点）。当我们去掉一个叶节点时，其父节点（假设为度为2）失去一个子节点，从而使其度降为1。为了恢复这个父节点的度为2，我们需要去掉它的另一个子节点（也是一个叶节点）。这样，我们总共去掉了两个叶节点，以及一个度为2的节点。由此可见，减少一个叶节点需要同时去掉一个度为2的节点，叶节点总数减少的数量与度为2节点减少的数量相同。

综合以上两个操作，我们可以得出结论：在任何二叉树中，增加一个度为2的节点会导致叶节点总数增加1，而减少一个叶节点则会导致叶节点总数减少1，并同时减少一个度为2的节点。因此，叶节点数（n0）与度为2的节点数（n2）之间始终保持恒定的关系：n0 = n2 + 1。

这个性质表明，在任何二叉树中，叶节点数总是比度为2的节点数多1。无论二叉树的具体形态如何变化，只要其叶节点数和度为2的节点数确定，两者之间的这种数量关系始终保持不变。

性质4：对于任何非空二叉树，其总结点数 n 总是等于叶节点数 n0​ 加上度为1的节点数 n1​ 加上度为2的节点数 n2​，则有：n=n0+n1+n2。

性质5: 具有n个结点的完全二叉树的深度为 floor(log2n) + 1。

这个性质描述了具有n个节点的完全二叉树的深度（即层数）与其节点总数n之间的关系。完全二叉树是一种特殊的二叉树，除了可能的最后一层外，每一层都被完全填满，并且最后一层的节点都尽可能靠左排列。

要理解这个性质，可以考虑完全二叉树的节点分布特点以及节点总数与深度之间的指数关系。在完全二叉树中，第i层（从根节点所在的第1层开始计数）最多有2^(i-1)个节点。随着层数i的增加，每层的节点数按指数级增长（即每增加一层，节点数翻倍）。当二叉树深度为h时，其节点总数最多为：

∑(2^(i-1)) for i = 1 to h = 2^0 + 2^1 + 2^2 + … + 2^(h-1) = 2^h - 1

这意味着，对于具有n个节点的完全二叉树，其节点总数n应满足以下关系：

2^(h-1) ≤ n < 2^h

取对数，得到：

h - 1 ≤ log2(n) < h

移项并取整数部分（向下取整），得到深度h为：

h = floor(log2(n)) + 1

因此，具有n个节点的完全二叉树的深度为 floor(log2n) + 1。这个性质揭示了完全二叉树节点总数与深度之间的对数关系，有助于我们快速估算或计算完全二叉树的深度，特别是在处理与完全二叉树相关的算法和数据结构问题时。

性质6: 对于一棵n个结点的完全二叉树，对任一个结点(编号为i)，有以下关系：

1. 如果i=1, 则结点i为根, 无父结点; 如果i>1, 则其父结点编号为 floor(i/2)。

在完全二叉树中，节点编号通常按照层序遍历的顺序进行。根节点编号为1，其子节点分别为2和3。对于任意节点i（i>1），其父节点的编号为其编号除以2向下取整，即floor(i/2)。这是因为完全二叉树中，每个节点的编号恰好是其左孩子的两倍，右孩子的两倍加1。因此，除以2并向下取整可得到父节点的编号。

举例说明：

对于如下完全二叉树：

        1
       / \
      2   3
     / \
    4   5

• 根节点编号为1，无父节点。
• 节点2的父节点编号为 floor(2/2) = 1，即根节点。
• 节点3的父节点编号为 floor(3/2) = 1，即根节点。
• 节点4的父节点编号为 floor(4/2) = 2，即节点2。
• 节点5的父节点编号为 floor(5/2) = 2，即节点2。

2. 如果 2i > n, 则结点i无子节点, 即结点i为叶结点; 否则左孩子编号为2i。

判断节点i是否有左孩子，只需看是否存在编号为2i的节点。如果2i大于总节点数n，说明不存在编号为2i的节点，因此节点i没有左孩子，即为叶节点。反之，如果2i≤n，说明存在编号为2i的节点，它是节点i的左孩子。

举例说明：

对于如下完全二叉树，节点总数n为5。

        1
       / \
      2   3
     / \
    4   5

• 节点1的左孩子编号为2i = 2 × 1 = 2，存在节点2，所以节点1有左孩子。
• 节点2的左孩子编号为2i = 2 × 2 = 4，存在节点4，所以节点2有左孩子。
• 节点3的左孩子编号为2i = 2 × 3 = 6，不存在节点6（因为n=5），所以节点3无左孩子，即为叶节点。
• 节点4的左孩子编号为2i = 2 × 4 = 8，不存在节点8（因为n=5），所以节点4无左孩子，即为叶节点。
• 节点5的左孩子编号为2i = 2 × 5 = 10，不存在节点10（因为n=5），所以节点5无左孩子，即为叶节点。

3. 如果 2i+1 > n, 则结点i无右孩子, 否则右孩子编号为2i+1。

类似地，判断节点i是否有右孩子，只需看是否存在编号为2i+1的节点。如果2i+1大于总节点数n，说明不存在编号为2i+1的节点，因此节点i没有右孩子。反之，如果2i+1≤n，说明存在编号为2i+1的节点，它是节点i的右孩子。

举例说明：

对于如下完全二叉树，节点总数n为5。

        1
       / \
      2   3
     / \
    4   5

• 节点1的右孩子编号为2i+1 = 2 × 1 + 1 = 3，存在节点3，所以节点1有右孩子。
• 节点2的右孩子编号为2i+1 = 2 × 2 + 1 = 5，存在节点5，所以节点2有右孩子。
• 节点3的右孩子编号为2i+1 = 2 × 3 + 1 = 7，不存在节点7（因为n=5），所以节点3无右孩子。
• 节点4的右孩子编号为2i+1 = 2 × 4 + 1 = 9，不存在节点9（因为n=5），所以节点4无右孩子。
• 节点5的右孩子编号为2i+1 = 2 × 5 + 1 = 11，不存在节点11（因为n=5），所以节点5无右孩子。

以上就是性质5中关于完全二叉树中任一节点与其父节点、子节点之间的编号关系的详细解释。这些关系有助于我们根据节点编号快速确定其在完全二叉树中的位置、父节点和子节点。

四、练习

1. 问题:二叉树和树有哪些不同?

2. 问题:具有3个结点的二叉树可能有____________种不同形态?请分别画出它们。

3. 问题:一棵完全二叉树有 5000个结点，可以计算出其叶结点的个数是_______________。

4. 问题:一棵深度为k且有__________个结点的二叉树称为满二叉树。

5. 问题:一颗深度为k的二叉树，至少有_____________个结点。

五、总结

综上所述，本篇文章围绕二叉树这一核心概念，从定义、分类到基本性质，构建了一个全面的知识框架。五条基本性质的阐述，不仅揭示了二叉树内部数量关系的稳定性与规律性，也展现了完全二叉树在深度计算、节点编号与父子关系定位上的独特优势。无论是对初学者奠定扎实基础，还是对进阶者深化理解与拓展应用，本篇关于二叉树的探讨都将起到积极的引导与促进作用。

六、感谢

如若本文对您的学习或工作有所启发和帮助，恳请您给予宝贵的支持——轻轻一点，为文章点赞；若觉得内容值得分享给更多朋友，欢迎转发扩散；若认为此篇内容具有长期参考价值，敬请收藏以便随时查阅。

每一次您的点赞、分享与收藏，都是对我持续创作和分享的热情鼓励，也是推动我不断提供更多高质量内容的动力源泉。期待我们在下一篇文章中再次相遇，共同攀登知识的高峰！