验证二叉树的前序序列化

题目要求

解题思路

方法一：栈
栈的思路是「自底向上」的想法。下面要结合本题是「前序遍历」这个重要特点。

我们知道「前序遍历」是按照「根节点-左子树-右子树」的顺序遍历的，只有当根节点的所有左子树遍历完成之后，才会遍历右子树。对于本题的输入，我们可以先判断「左子树」是否有效的，然后再判断「右子树」是否有效的，最后判断「根节点-左子树-右子树」是否为有效的。这个思路类似于递归，而把递归改写成循环时，就会使用「栈」，这就是本题使用「栈」的原因。

下面的重点是如何判断一棵子树是否有效？首先考虑最简单情况：怎么判断一个节点是叶子节点？很明显，当一个节点的两个孩子都是 "#"（空）的时候，该节点就是叶子节点。

当一个节点不是叶子节点的时候，那么它必定至少有一个孩子非空！有两种情况：

两个孩子都非"#"（空）；
一个孩子为"#"（空），另一个孩子非"#"（空）；
为了兼容这两个情况，我们想出了本题的一个重磅级的技巧：把有效的叶子节点使用 "#" 代替。 比如把 4## 替换成 # 。此时，叶子节点会变成空节点！

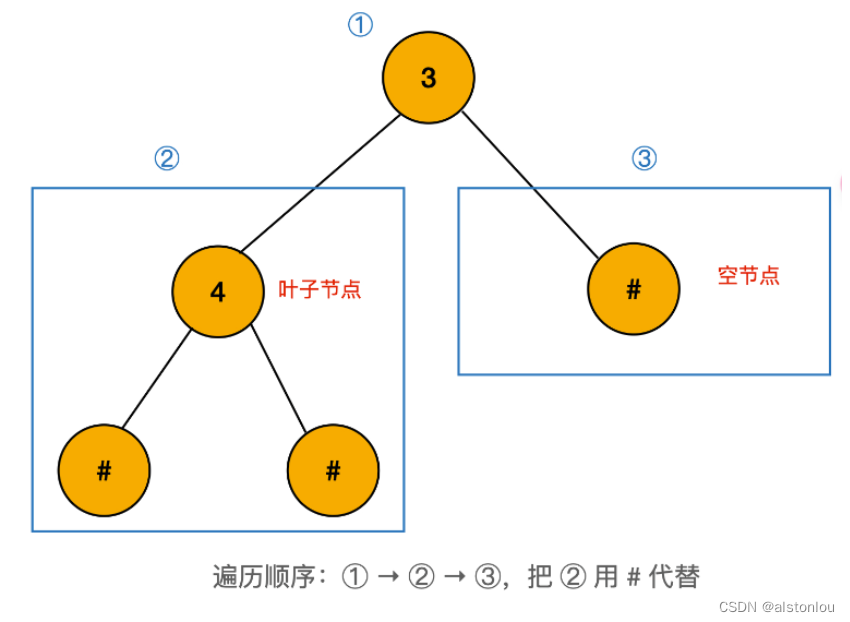
具体操作流程示例如下：

如输入："9,3,4,#,#,1,#,#,2,#,6,#,#"，当遇到 x,#,# 的时候，就把它变为 #。

模拟一遍过程：

1. [9,3,4,#,#] => [9,3,#]，继续
2. [9,3,#,1,#,#] => [9,3,#,#] => [9,#] ，继续
3. [9,#2,#,6,#,#] => [9,#,2,#,#] => [9,#,#] => [#]，结束

方法二：计算入度出度

背景知识：

• 入度：有多少个节点指向它；
• 出度：它指向多少个节点。

我们知道在树（甚至图）中，所有节点的入度之和等于出度之和。可以根据这个特点判断输入序列是否为有效的！

在一棵二叉树中：

• 每个空节点（ "#"）会提供 0 个出度和 1 个入度。
• 每个非空节点会提供 2 个出度和 1 个入度（根节点的入度是 0）。

我们只要把字符串遍历一次，每个节点都累加 diff = 出度 - 入度 。在遍历到任何一个节点的时候，要求diff >= 0，原因是还没遍历到该节点的子节点，所以此时的出度应该大于等于入度。当所有节点遍历完成之后，整棵树的 diff == 0。

这里解释一下为什么下面的代码中 diff 的初始化为 1。因为，我们加入一个非空节点时，都会对 diff 先减去 1（入度），再加上 2（出度）。但是由于根节点没有父节点，所以其入度为 0，出度为 2。因此 diff 初始化为 1，是为了在加入根节点的时候，diff 先减去 1（入度），再加上 2（出度），此时 diff 正好应该是2.

代码

方法一：

class Solution(object): 
    def isValidSerialization(self, preorder): 
        stack = [] 
        for node in preorder.split(','): 
            stack.append(node) 
            while len(stack) >= 3 and stack[-1] == stack[-2] == '#' and stack[-3] != '#': 
            stack.pop(), stack.pop(), stack.pop() 
            stack.append('#') 
        return len(stack) == 1 and stack.pop() == '#' 

方法二：

class Solution(object): 
    def isValidSerialization(self, preorder): 
    nodes = preorder.split(',') 
    diff = 1 
    for node in nodes: 
        diff -= 1 
        if diff < 0: 
            return False
        if node != '#': 
            diff += 2 
    return diff == 0 

复杂度分析

方法一：

• 时间复杂度：$O(N)$
• 空间复杂度：$O(N)$

方法二：

• 时间复杂度：$O(N)$
• 空间复杂度：$O(1)$

参考

负雪明烛