几何分类

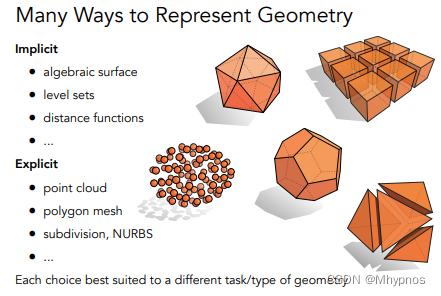
几何分类：隐式几何和显示几何

隐式几何：不会告诉空间中的点具体在哪，告诉这些点满足的一定关系。
如球的描述 $x^2+y^2+z^2=1$

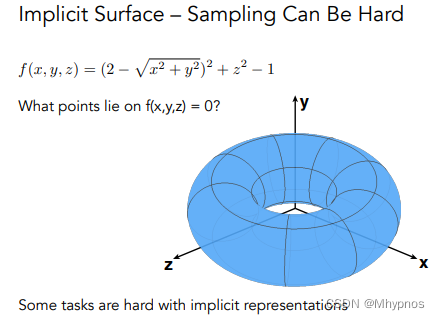
缺点：这个面都有哪些点是不容易看出来的，从上述的式子里很难看出是个圆环的结构。

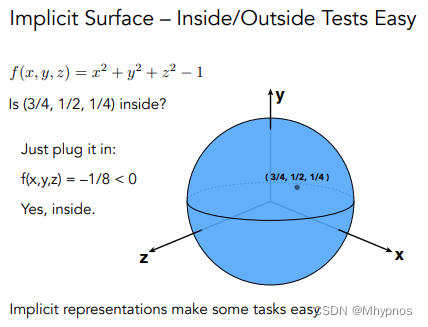
优点：容易判断点在不在面上. 等于0在表面上，小于0在物体内，大于0在物体外

显式几何：直接给出点的位置，如之前模型上直接给出三角形的点。另一种是通过参数映射的方法定义表面。
如上图定义了一个空间uv，上面任何一个点都用坐标(u,v)表示，并且这个点都会映射对应到空间中的某一点。
则可以定义一个函数，输入的是u，v，输出的是x，y，z。
把所有的(u,v)找一遍，可以找到对应的所有的(x,y,z)。

优点：显示形状很容易

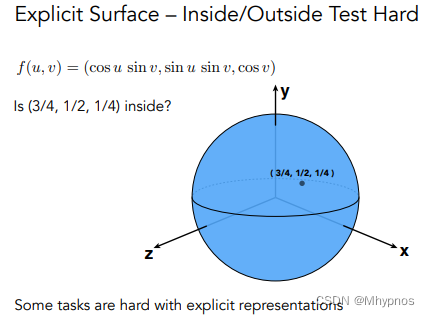
缺点：不容易判断点与表面的关系

More Implicit Representations in Computer Graphics

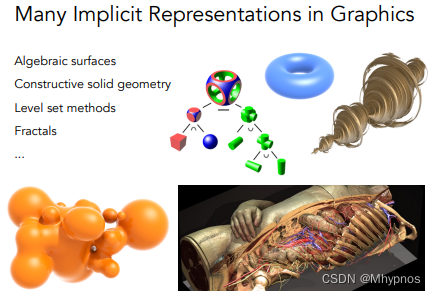
更多得隐式几何表现方法

直接用数学公式表示，最大得问题是不直观

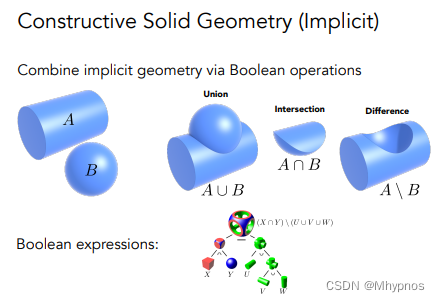
CSG：通过一系列基本几何的基本运算，来定义新的几何。通过简单的几何来形成复杂的几何

距离函数：空间中的任意一个点，到你想要表述的几何形体上面任一点，他们直接的最小距离，正负都可以。如果点在几何形体的外面，则距离为正，如果点在物体内部，则距离为负。
如上图，两个球在相互接近时，形状发生了变换。把两个不同物体的，他们两者的距离函数都算出来之后，把两个距离函数做一个blending，融合。再恢复成原来的物体

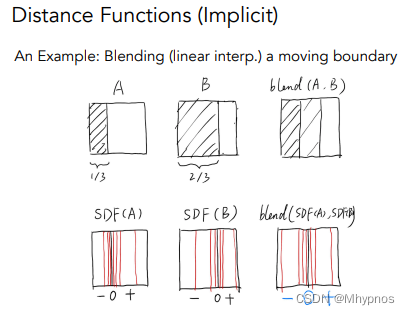
应用距离函数的例子。输入和输出是两张不同的图，认为他们是一个表示某种几何的边界。有一个物体挡住了视口的1/3，另外一个物体经过了一些移动之后，挡住了2/3。希望求出物体从左到右移动的一个中间状态。
我们期望的结果是blend的新图，左边一半是黑的，右边一半是白，因为是运动信息的中间态。但现在结果是左边1/3是黑的，中间1/3是灰的，右边1/3是白的
则需要先求出距离函数。物体的边界(SDF(A)中间那条黑线)我们认为就是物体的表面（A图中黑色运动物体的边界），则靠近这个边界的点的值是比较小大，远离这个边界的值是比较大的。对于B同理。把这两张图进行blend操作，得到的边界(0)在正中，再通过SDF恢复成原本的形状。
通过blend两个对应的SDF，等于blend物体的边界

分别把两个物体对应的距离函数求出来，即空间中任意一个点他们对应的距离函数，然后blend起来。再恢复成原本的面。即SDF值是0的时候，就是物体的面所在的地方

距离函数应用的例子

距离函数恢复成物体的表面，取所有距离等于0的点就是物体的表面。
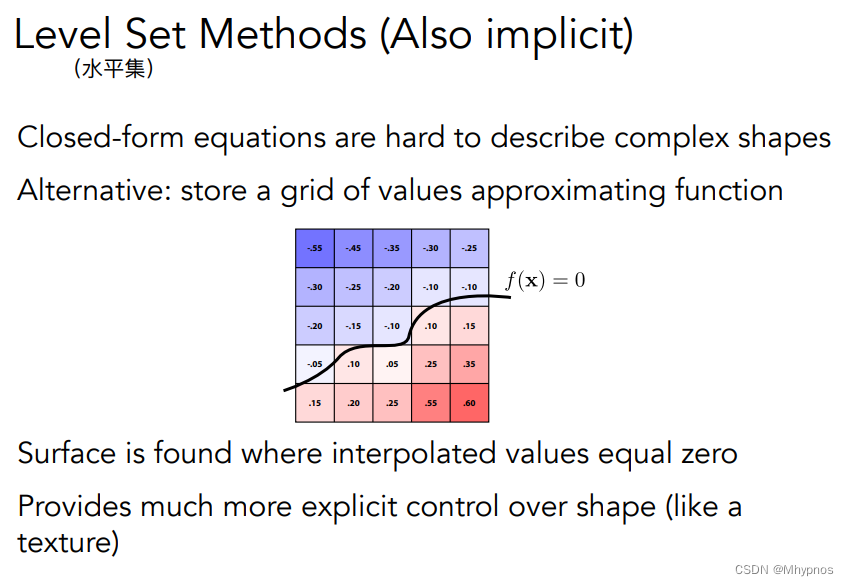
对于一些特点的情况。距离函数不太好写成某一种解析的式子 f(x) 的形式，只要距离函数能通过某种方法表述起来就行。
如上图，水平集方法：函数的表述是写在一个格子上的，函数在不同的地方有不同的值，水平集是在一个格子上的不同位置写好他的值是多少。只需要找到在中间某些值是0的地方，就可以提取函数所试图描述的表面。
类似地理上的等高线。
可以通过双线性插值解出等于0的位置

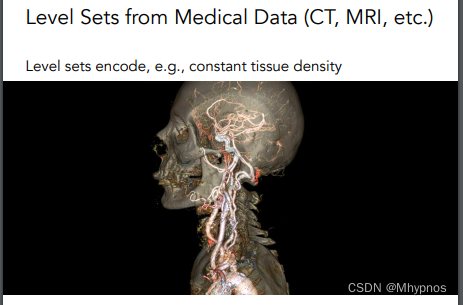
水平集可以定义在3维空间上的格子。
则如果有一3维纹理，表示人体的不同位置的密度。
如何从3维的信息提取出物体的表面：可以让密度的函数 f(x) 等于某个密度，如5.0，找到所有这样满足这个密度的位置，则可以找到一个表面

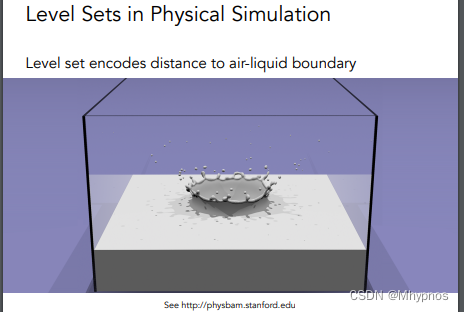
水花和水花结合在一块，也可以通过距离函数，水平集来描述。把水滴和水滴blend在一块，再提出融合到一块之后的表面

分形：自相似的意思，自己的一个部分和整体长的非常像。类似递归。
如雪花

优点：

1. 隐式的函数通常表述起来都很容易。正常情况下都不是明确地把表面上的点写出来，存储比较容易
2. 可以查询在表面的里外。
3. 容易做光线求交
4. 能严格的描述物体的弧度，适合描述拓扑结构等

缺点：

1. 难以描述复杂的模型形状

Explicit Representations in Computer Graphics

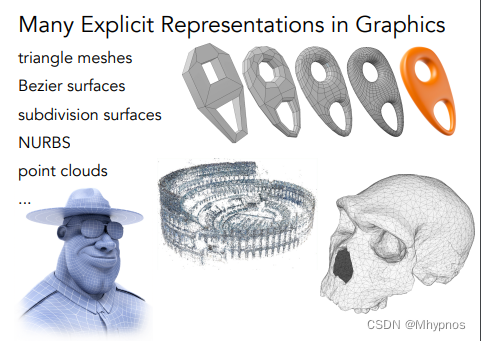
三角形面，贝塞尔曲面，点云。。。

点云：不考虑物体是一个表面，而是表面上的一堆点，把每个点都表示成一个点。只要点够细，就看不到点与点之间的缝隙，就可以看到一个表面的概念
即一个(x,y,z)的列表
通常人们做一个三维空间的扫描，得到的输出就是点云
点云经常在之后会处理成多边形的面

多边形面：四边形或三角形
要注意的是连接关系

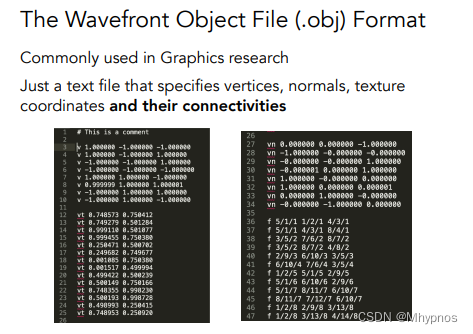
特定的文件格式：.obj，文本文件，存储的是空间中的一个物体。
把空间中的一堆点，一堆法线和一堆纹理坐标分开来表示，然后再一块组织起来
一个立方体：8个点v，6个法线vn（输出的时有冗余，29，30是同一法线），12个纹理坐标vt。
face定义连接关系(v，vt， vn)，即三角形面