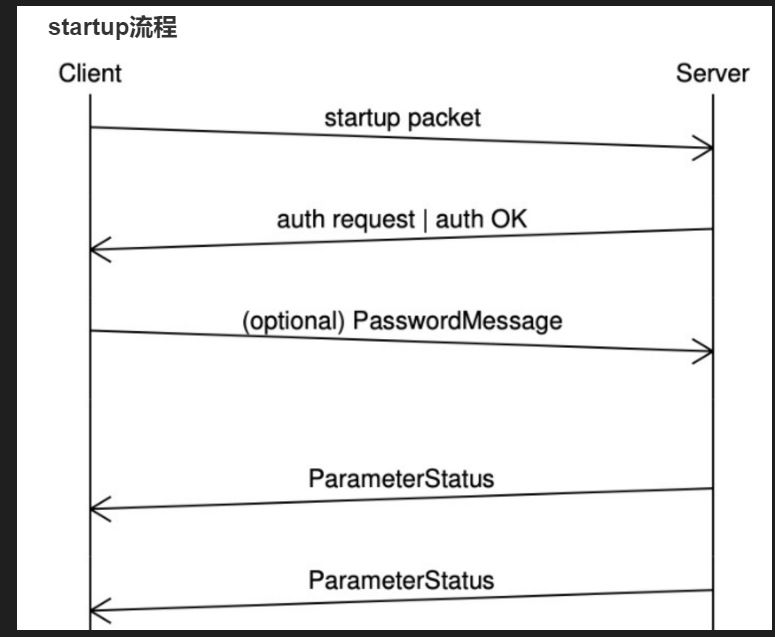
神经网络(NN)复杂度
- NN复杂度,多用NN层数和NN参数个数表示

如上图示
- 空间复杂度
- 层数=隐藏层的层数+1个输出层
- 上图为2层NN
- 总参数
- 3*4+4 +4*2+2=26
- 层数=隐藏层的层数+1个输出层
- 时间复杂度
- 乘加运算次数
- 3*4+4*2=20
- 乘加运算次数
指数衰减学习率
可以先用较大学习率,快速得到较优解,然后逐步减小学习率,使模型在训练后期稳定
指数衰减学习率
=
初始学习率
∗
学习率衰减
率
当前轮数
/
多少轮衰减一次
指数衰减学习率=初始学习率*学习率衰减率^{当前轮数/多少轮衰减一次}
指数衰减学习率=初始学习率∗学习率衰减率当前轮数/多少轮衰减一次
激活函数
-
sigmoid
- f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
- 易造成梯度消失
- 输出非0均值,收敛慢
- 幂运算复杂,训练时间长
-
Tanh函数
- f ( x ) = 1 − e − 2 x 1 + e − 2 x f(x)=\frac{1-e^{-2x}}{1+e^{-2x}} f(x)=1+e−2x1−e−2x
- 输出是0均值
- 易造成梯度消失
- 幂运算复杂,训练时间长
-
Relu
- f ( x ) = m a x ( x , 0 ) f(x)=max(x,0) f(x)=max(x,0)
- 在正区间解决了梯度消失问题
- 计算速度快
- 收敛速度远快于Sigmoid和TanH
- 缺点
- 输出非0均值,收敛慢
- Dead Relu问题:某些神经元可能永远不会被激活,导致相应的参数永远无法更新
-
Leaky Relu
- tf.nn.leaky_relu(x)
- f(x)=max(ax,x)
- 不会有Dead Relu问题,但是实际操作中,并没有完全证明Leaky Relu总是好于Relu

初学者建议
- 首选Relu激活函数
- 学习率设置较小值
- 输入特征标准化
- 初始参数中心化,即让随机生成的参数满足正态分布,且 m e a n = 0 , s t d d e v = 2 当前层输入特征个数 mean=0, stddev=\sqrt{\frac{2}{当前层输入特征个数}} mean=0,stddev=当前层输入特征个数2
损失函数Loss
预测值y与已知答案y_的差距
nn优化目标:loss最小
-
均方误差 MSE
m s e ( y _ , y ) = ∑ i = 1 n ( y − y _ ) 2 n mse(y\_,y)=\frac{\sum^n_{i=1}(y-y\_)^2}{n} mse(y_,y)=n∑i=1n(y−y_)2loss_mse=tf.reduce_mean(tf.square(y_-y)) -
交叉熵损失函数CE
- Cross Entropy:表征两个概率分布之间的距离
H ( y , y ) = − ∑ y _ ∗ l n y H(y_,y)=- \sum y\_*lny H(y,y)=−∑y_∗lny
tf.losses.categorical_crossentropy(y_,y)示例:二分类,已知答案y_=(1,0),预测y1=(0.6,0.4),y2=(0.8,0.2),哪个更接近标准答案?
H 1 ( ( 1 , 0 ) , ( 0.6 , 0.4 ) ) = − ( 1 ∗ l n 0.6 + 0 ∗ l n 0.4 ) ≈ 0.511 H 2 ( ( 1 , 0 ) , ( 0.8 , 0.2 ) ) = − ( 1 ∗ l n 0.8 + 0 ∗ l n 0.2 ) ≈ 0.223 H_1((1,0),(0.6,0.4))=-(1*ln0.6+0*ln0.4)\approx0.511\\ H_2((1,0),(0.8,0.2))=-(1*ln0.8+0*ln0.2)\approx0.223 H1((1,0),(0.6,0.4))=−(1∗ln0.6+0∗ln0.4)≈0.511H2((1,0),(0.8,0.2))=−(1∗ln0.8+0∗ln0.2)≈0.223
因为 H 1 > H 2 H_1>H_2 H1>H2,所有y2预测更准。
欠拟合与过拟合
欠拟合的解决方法
- 增加输入特征项
- 增加网络参数
- 减少正则化参数
过拟合的解决方法
- 数据清洗
- 增大训练集
- 采用正则化
- 增大正则化参数
正则化
正则化在损失函数中引入模型复杂度指标,利用给w的加权值,弱化了训练数据的噪声,一般不正则化b
l
o
s
s
=
l
o
s
s
(
y
,
y
)
+
R
E
G
U
L
A
R
I
Z
E
R
∗
l
o
s
s
(
w
)
loss=loss(y_,y)+REGULARIZER*loss(w)
loss=loss(y,y)+REGULARIZER∗loss(w)
L1正则化
l
o
s
s
L
1
=
∑
i
∣
w
i
∣
loss_{L1}=\sum_i|w_i|
lossL1=i∑∣wi∣
L2正则化
l
o
s
s
L
2
=
∑
i
∣
w
i
2
∣
loss_{L2}=\sum_i|w^2_i|
lossL2=i∑∣wi2∣
正则化的选择
- L1正则化大概率会使 很多参数变为零,因此该方法可通过稀疏参数,即减少参数的数量,降低复杂度
- L2正则化会使参数很接近零但不为零,因此该方法可以通过减少参数的值的大小降低复杂度
参数优化器
整体优化流程
待优化参数w,损失函数loss,学习率lr,每次迭代一个batch,t表示当前batch迭代的总次数:
- 计算 t t t时刻损失函数关于当前参数的梯度 g t = Δ l o s s = ∂ l o s s ∂ ( w t ) g_t=\Delta loss=\frac{\partial loss}{\partial (w_t)} gt=Δloss=∂(wt)∂loss
- 计算 t t t时候一阶动量 m t m_t mt和二阶动量 V t V_t Vt
- 计算 t t t时刻的下降梯度 η t = l r ⋅ m t / V t \eta_t=lr·m_t/\sqrt{V_t} ηt=lr⋅mt/Vt
- 计算 t + 1 t+1 t+1时刻参数: w t + 1 = w t − η t w_{t+1}=w_t-\eta_t wt+1=wt−ηt
注意:
一阶动量:与梯度相关的函数
二阶动量:与梯度平方相关的函数
神经网络训练时为了提高效率,每次喂入batch个数据,每个batch是 2 n 2^n 2n个数据
SGD 随机梯度下降
- 常用的地图下降法
- m t = g t m_t=g_t mt=gt
- V t = 1 V_t=1 Vt=1
SGDM
- 含momentum的SGD,在SGD基础上增加一阶动量
-
m
t
=
β
⋅
m
t
−
1
+
(
1
−
β
)
⋅
g
t
m_t=\beta·m_{t-1}+(1-\beta)·g_t
mt=β⋅mt−1+(1−β)⋅gt
- m t m_t mt表示各时刻梯度方向的指数滑动平均值
- β \beta β的经验值为0.9
- V t = 1 V_t=1 Vt=1
Adagrad
- 在SGD基础上增加二阶动量
- 可以对模型中的每个参数分配自适应学习率
- m t = g t m_t=g_t mt=gt
- V t = Σ τ = 1 t g τ 2 V_t=\Sigma^t_{\tau=1}g^2_\tau Vt=Στ=1tgτ2
RMSProp
- 在SGD基础上增加二阶动量
- m t = g t m_t=g_t mt=gt
- V t = β ⋅ V t − 1 + ( 1 − β ) ⋅ g t 2 V_t=\beta·V_{t-1}+(1-\beta)·g_t^2 Vt=β⋅Vt−1+(1−β)⋅gt2
Adam
- 同时结合SGDM的一阶动量和RMSProp的二阶动量
-
m
t
=
β
1
⋅
m
t
−
1
+
(
1
−
β
1
)
⋅
g
t
m_t=\beta_1·m_{t-1}+(1-\beta_1)·g_t
mt=β1⋅mt−1+(1−β1)⋅gt
- 修正一阶动量的偏差 m t ^ = m t 1 − β 1 t \hat{m_t}=\frac{m_t}{1-\beta_1^t} mt^=1−β1tmt
-
V
t
=
β
2
⋅
V
t
−
1
+
(
1
−
β
2
)
⋅
g
t
2
V_t=\beta_2·V_{t-1}+(1-\beta_2)·g_t^2
Vt=β2⋅Vt−1+(1−β2)⋅gt2
- 修正二阶动量的偏差 V t ^ = V t 1 − β 2 t \hat{V_t}=\frac{V_t}{1-\beta_2^t} Vt^=1−β2tVt