思路：BFS

这道BFS可谓是细节爆炸，对于编程能力和判断条件的能力的考察非常之大。

对于这道题，我们还需要额外考虑一些因素，那就是对于障碍物的考虑和机器人方位的考虑。

首先我们看第一个问题，就是对于障碍物的考虑，这里转载一下洛谷某一位大佬的图像：

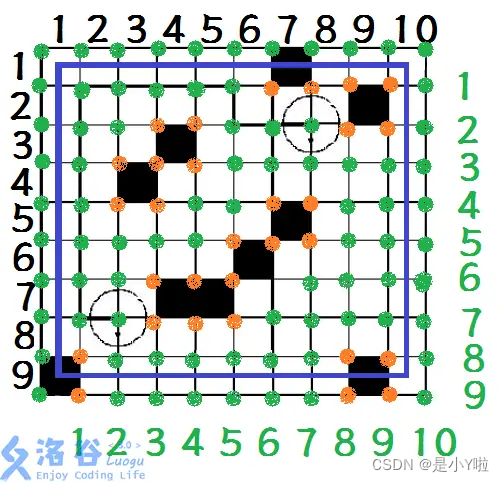
绿色的结点就是机器人走的结点，但是黑色的方块却是障碍物的地方。这就很矛盾，因为明明机器人走的是点，但是障碍物是以方块的形式呈现的。所以我们不得不想，怎么样才能处理这种关系呢？根据这样的图像呈现，我们可以知道，在蓝色方框之内的绿色结点才是机器人能够走的结点。因为在边界处，我们的机器人并不能走，因为自身就拥有宽度，所以我们在之后判断边界的时候需要额外注意，不能碰到边界位置。

根据黑色方块的位置坐标，我们可以转化成机器人不能走的结点在哪。那么上面的橙色结点就是机器人在障碍物的时候不能走的结点了。下结论来说，这个样例中机器人能够走的地方就是蓝色方框以内绿色结点的位置，且不会波及到橙色结点的地方。这里需要处理一下，也就是对于这个结点的处理。

接下来，我们再看第二个问题，机器人的方位怎么考虑？并且，我们在转动的时候是需要花费时间的，怎么样才能在转到某个方位的同时，花费少的时间呢？这里在代码中定义了几个数组：

dx:在x轴方向的行走，下标从1开始；

dy:同理在y轴方向的行走；

dt:顺时针方向上各个方向的编号；

dtt:数字i在dt数组中所对应的下标

abc:转动i次到达的方向所需要的最少旋转次数。

这里的abc数组可能难理解一些。

举个例子：你在北方向，北方向对应的编号是1，我们旋转i次，假设i=3(假设我们都是顺时针旋转），这个时候我们是不是旋转到了西方向呢？也就是当我们旋转到这个方向，顺时针我们用了3次，但是最小用的旋转次数其实就是逆时针旋转了1次，这个dtt数组存储的就是1，这就是这个数组的作用，解决了旋转次数最少的问题，也就是花费时间尽可能少的原则。

好了，这样我们就开始BFS遍历就行了。

注意：有几个特判需要知道：终点和起点可能会重合；终点是1的时候，肯定不能到；起点可能也有障碍物。

上代码：

#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<cmath> 
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>
#include <iomanip>
#include<sstream>
#include<numeric>
#include<map>
#include<limits.h>
#include<unordered_set>
#include<set>
#define int long long
#define MAX 501
#define _for(i,a,b) for(int i=a;i<(b);i++)
#define ALL(x) x.begin(),x.end()
using namespace std;
typedef pair<int, int> PII;
int n, m;
int counts;
int maps[MAX][MAX];//地图原先的构造
int a[MAX][MAX];//机器人能走的结点标志，1为不能走，0为能走
int dx[5] = { 0,-1,1,0,0 };
int dy[5] = { 0,0,0,-1,1 };
int dt[5] = { 0,1,4,2,3 };//方位
int dtt[5] = { 0,1,3,4,2 };//数字i在dt中的下标
int abc[5] = { 0,1,2,1,0 };//顺时针旋转到这个方位所需要的最小次数
int stx, sty;
int edx, edy;
struct Node {
    int x;
    int y;
    int t;//机器人的方位
    int times;//到达这里的最少时间
};
queue<Node>q;
char ch;
int direct;//最开始的方位
int flag = false;
void fangwei() {//标记方位号
    switch (ch) {
    case 'N':
        direct = 1;
        break;
    case 'S':
        direct = 2;
        break;
    case 'W':
        direct = 3;
    case 'E':
        direct = 4;
        break;
    }
    return;
}
void turn_into() {//根据原地图判断机器人能走的地方
    _for(i, 1, n + 1) {
        _for(j, 1, m + 1) {
            if (maps[i][j] == 1) {
                a[i - 1][j] = 1;
                a[i][j - 1] = 1;
                a[i - 1][j - 1] = 1;
                a[i][j] = 1;
            }
        }
    }
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);
    cin >> n >> m;
    _for(i, 1, n + 1) {
        _for(j, 1, m + 1) {
            cin >> maps[i][j];
        }
    }
    _for(i, 1, n + 1) {
        _for(j, 1, m + 1) {
            if (maps[i][j] == 1)
                flag = 1;
        }
    }
    cin >> stx >> sty >> edx >> edy;
    cin >> ch;
    fangwei();
    turn_into();
    Node firsts;//the first one
    firsts.x = stx;
    firsts.y = sty;
    firsts.t = direct;
    firsts.times = 0;
    q.push(firsts);
    while (!q.empty()) {
        auto tmp = q.front();
        q.pop();
        _for(i, 1, 5) {
            int zhuan = abc[i];//转动i次所得的方位的最小次数
            int fangw = dtt[tmp.t] + i;//本来的方位+i,也就是现在旋转之后的方位
            if (fangw == 5)fangw = 1;
            if (fangw == 6)fangw = 2;
            if (fangw == 7)fangw = 3;
            if (fangw == 8)fangw = 4;
            fangw = dt[fangw];
            _for(j, 1, 4) {
                int zoux = tmp.x + dx[fangw] * j;
                int zouy = tmp.y + dy[fangw] * j;
                if (zoux <= 0 || zoux >= n || zouy <= 0 || zouy >= m || (zoux == stx && zouy == sty) || a[zoux][zouy]==1)
                {
                    break;
                }
                if ((tmp.times + zhuan + 1 < maps[zoux][zouy] || maps[zoux][zouy] == 0) && a[zoux][zouy] == 0) {
                    Node d;
                    d.x = zoux;
                    d.y = zouy;
                    d.t = fangw;
                    d.times = tmp.times + zhuan + 1;
                    maps[zoux][zouy] = d.times;//flag
                    q.push(d);
                }
            }
        }
    }
    
    if ((maps[edx][edy] == 0 && (edx != stx && edy != sty)) || (maps[edx][edy] == 1))
        cout << -1 << endl;
    else if (n == 50 && m == 50 && flag == 0)
        cout << maps[edx][edy] + 1 << endl;
    else
        cout << maps[edx][edy] << endl;
    return 0;
}