题目一

方法一

归并分治

代码：

# include <stdio.h>

int arr[100];
int help[100];

int n;

//归并分治
// 1.统计i、j来自 l~r 范围的情况下，逆序对数量
// 2.统计完成后，让arr[l...r]变成有序的 
int f(int l, int r)
{
	if (l == r)
		return 0;
	int m = (l + r) / 2;
	return f(l, m) + f(m+1, r) + merge(l, m, r);
}

int merge(int l, int m, int r)
{
	//i 来自 l...m
	//r 来自 m+1....r
	//统计有多少逆序对 
	int ans = 0;
	int j = r;
	for (int i=m; i>=l; --i)
	{
		while (j >= m+1 && arr[i] <= arr[j])
			j = j - 1;
		ans = ans + j - m;
	}
	
	//左右部分合并，整体变有序，归并排序的过程 
	int k = l;
	int a = l;
	int b = m + 1;
	while (a <= m && b <= r)
	{
		if (arr[a] <= arr[b])
		{
			help[k] = arr[a];
			a = a + 1;
		}
		else
		{
			help[k] = arr[b];
			b = b + 1;
		}
		k = k + 1;
	}
	while (a <= m)
	{
		help[k] = arr[a];
		k = k + 1;
		a = a + 1;
	}
	while (b <= m)
	{
		help[k] = arr[b];
		k = k + 1;
		b = b + 1;
	}
	for (i = l; i <= r; ++i)
		arr[i] = help[i];
	return ans; 
}

int main()
{
	scanf("%d", &n);
	for (int i=0; i<n; ++i)
		scanf("%d", &arr[i]);
	
	int ans = f(0, n-1);
}

方法二

树状数组

我们假设一个数组arr

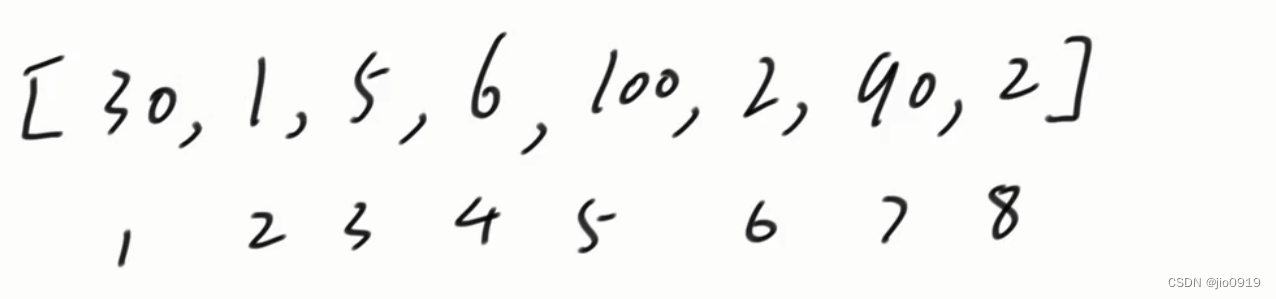
建立一个词频数组

用于记录数字出现的次数

因为arr数组中最大的数字为100

所以只要建立一个长度为100的词频数组即可

我们对原数组从右往左进行考虑

先考虑arr[8]（也就是2）

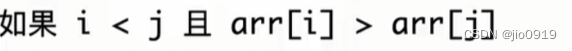
对于逆序对，i  <  j，并且arr[i] > arr[j]

因此我们只要统计小于2的数，在词频数组中的和即可

也就是词频数组中下标2之前的前缀和

在统计完sum后，再将2添加进词频数组中

这时，我们就可以把词频数组转为树状数组

以上的操作就变为了

单点修改和区间查询

注意：

此时要考虑树状数组长度的问题！！！

因为词频数组的长度是由原数组最大值决定的，可能会出现过大的情况

此时就要进行离散化处理！

我们可以假设另外一个数组help

将原数组按照从小到大的顺序填入help数组中

并进行去重（可以使用双指针）

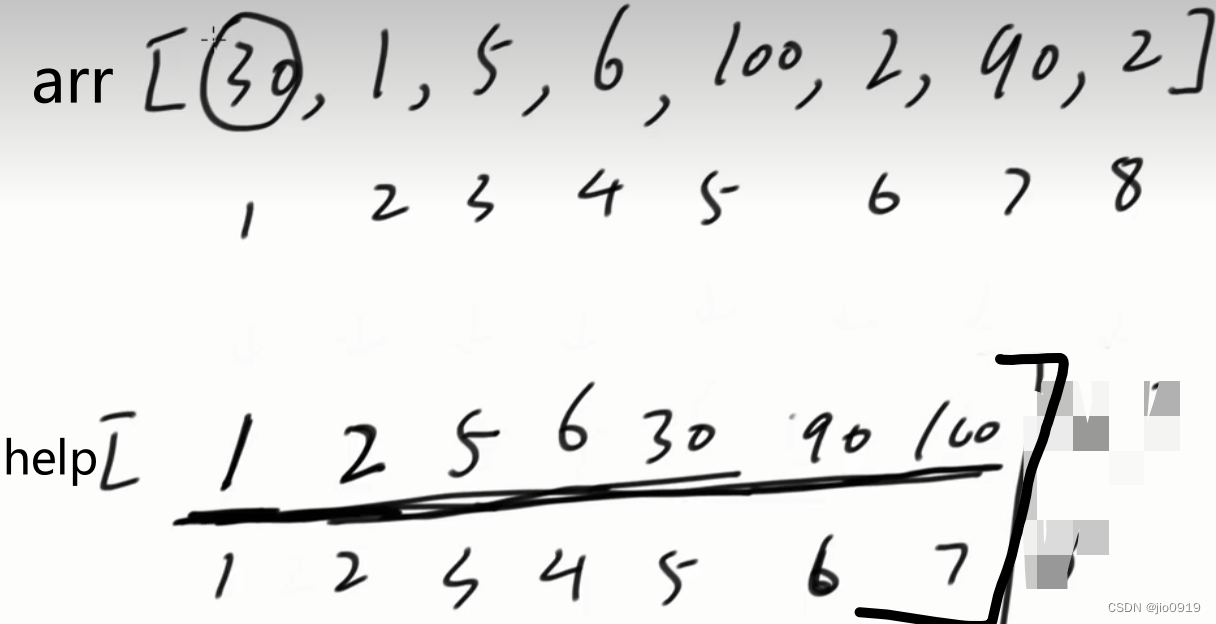
然后通过help数组对arr数组进行修改

利用二分

找到原数组中的数字在help数组中的下标位置

并将该数字修改为help数组中的下标的值

  

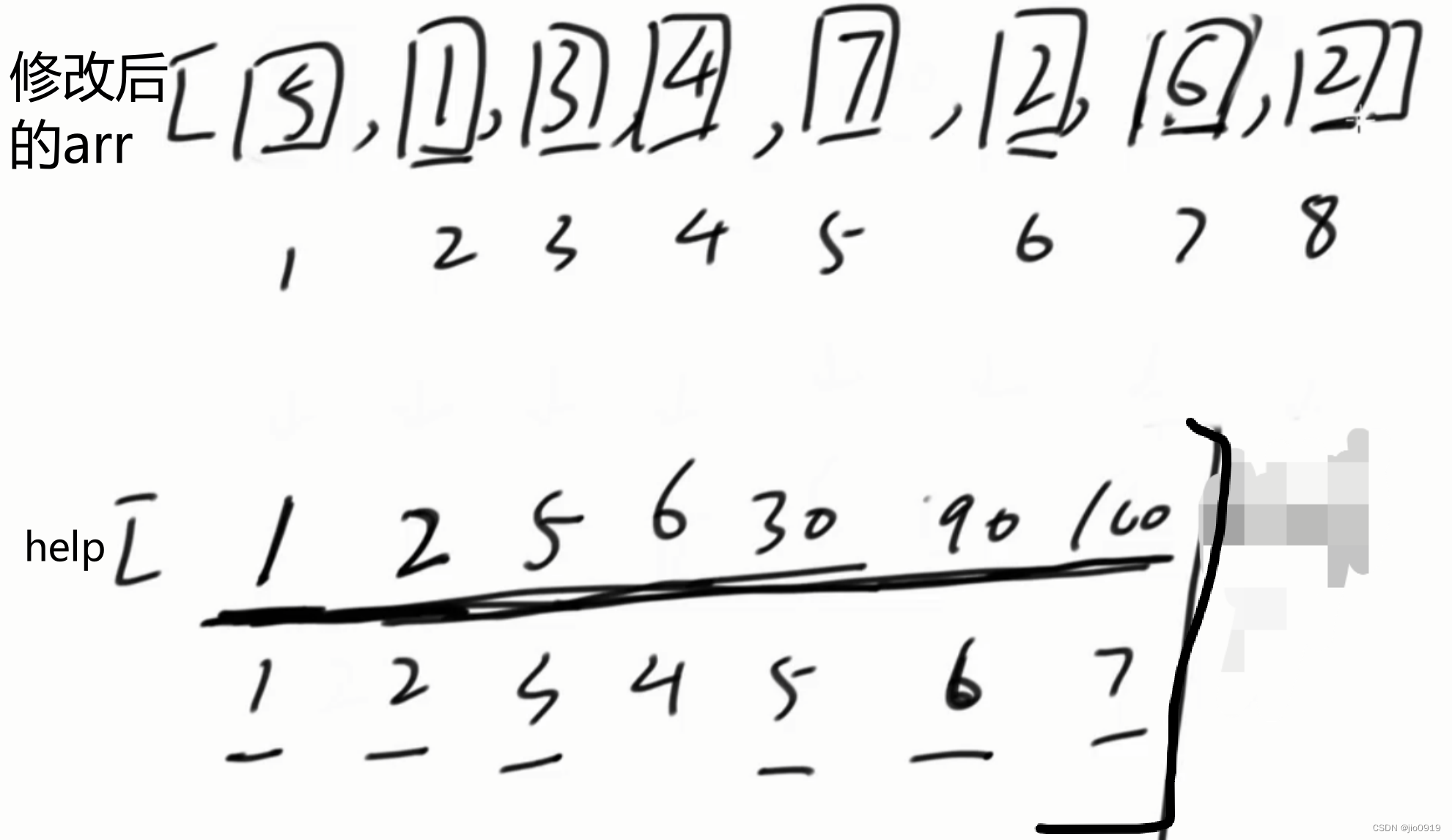
再对此时的arr数组进行词频统计建立树状数组

代码：

# include <stdio.h>
# include <stdlib.h>
int arr[100];
int sort[100];
int tree[100];

int n, m;

int cmp(const void* a, const void* b)
{
	int p1 = *(int*)a;
	int p2 = *(int*)b;
	return p1 - p2;
}

int lowbit(int x)
{
	return x & (-x);
}

void add(int i, int v)
{
	while (i <= m)
	{
		tree[i] = tree[i] + m;
		i = i + lowbit(x);
	}
}

int sum(int i)
{
	int ans = 0;
	while (i > 0)
	{
		ans = ans + tree[i];
		i = i - lowbit(i;)
	}
	return ans;
}


// 给定原始值v
// 返回sort数组中1~m的下标 
int rank(int v) 
{
	int l = 1;
	int r = m;
	int mid;
	int ans = 0;
	while (l<=r)
	{
		mid = (l + r) / 2;
		if (sort[mid] >= v)
		{
			ans = mid;
			r = mid - 1;
		}
		else
		{
			l = mid + 1;
		}
	}
	return ans;
}

int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i)
	{
		scanf("%d", arr[i]);
		sort[i] = arr[i];
	}
	qsort(sort, sizeof(int), n, cmp);
	m = 1;
	for (int i=2; i <= n; ++i)
	{
		if (sort[i] != sort[m])
		{
			m = m + 1;
			sort[m] = sort[i];
		}
	}
	int ans = 0;
	for (int i=1; i<=n; ++i)
		arr[i] = rank(arr[i]);
	
	for (int i=n; i>=1; --i)
	{
		//增加当前数字的词频 
		add(arr[i], 1);
		// 右边有多少数字是 <= 当前数值 - 1 
		ans = ans + sum(arr[i]-1);
	}
	printf("%d", ans);
}

两个方法的区别：

归并分治实现：无需离散化代码、使用空间少、常数时间优良，不能实时查询，只能是离线的批量过程

树状数组实现：需要离散化代码、使用空间多、常数时间稍慢，可以实时查询

题目二(典型)

我们建立两个数组up1， up2

up1[ i ]：以下标 i 做结尾的升序的只有一个元素的数量

up2[ i ]：以下标 i 做结尾的升序的含有两个元素的数量

假设数组arr为：

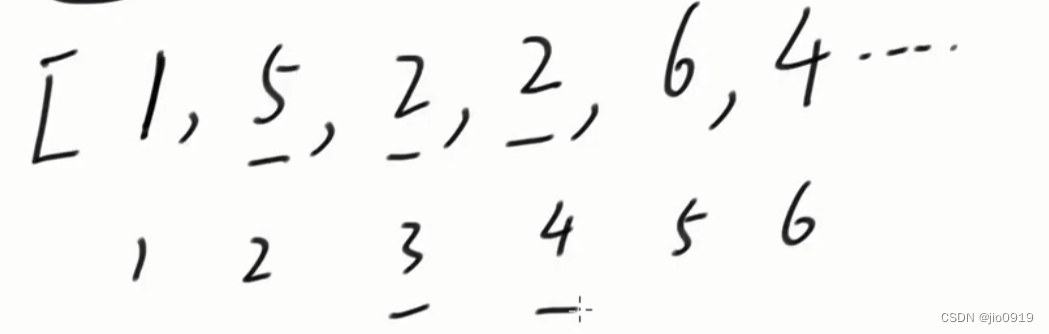
从左往右进行处理

我们加入第一个数字为arr[1] = 1

先判断以 1 做结尾的升序的含有三个元素的数量

我们发现该值就是在up2数组中小于1的前缀和

然后再更新以 1 做结尾的升序的含有两个个元素的数量（也就是up2[1]）

我们发现该值就是在up1数组中小于1的前缀和

找到该值后，填入up2[1]

更新以 1 做结尾的升序的含有一个元素的数量（也就是up1[1]）

依次对 arr 数组从左往右进行遍历

因此，我们先对数组中的元素进行离散化处理

然后从左往后按照上述步骤进行

代码：

# include <stdio.h>
# include <string.h>
//记录原数组 
int arr[100];

//建立去重离散化数组 
int sort[100];

//维护信息：up1
//tree1不是up1数组，是up1数组的树状数组 
int tree1[100]; 

//维护信息：up2
//tree2不是up2数组，是up2数组的树状数组 
int tree2[100];

int n, m;

int cmp(const void* a, const void* b)
{
    int* p1 = (int*)a;
    int* p2 = (int*)b;
    return *p1 - *p2;
}

int lowbit(int x)
{
	return x & (-x);
}

void add(int* tree, int i, int v)
{
	while (i <= m)
	{
		tree[i] = tree[i] + v;
		i = i + lowbit(i);
	}
}

int sum(int* tree, int i)
{
	int ans = 0;
	while (i > 0)
	{
		ans = ans + tree[i];
		i = i - lowbit(i);
	}
	return ans;
}

int rank(int x)
{
	int l = 1;
	int r = m;
	int mid;
	int ans = 0;
	while (l <= r)
	{
		mid = (l + r) / 2;
		if (sort[mid] >= v)
		{
			ans = mid;
			r = mid - 1;
		}
		else	
			l = mid + 1;
	}
	return ans;
}

int main()
{
	scanf("%d", &n);
	for (int i=1; i<=n; ++i)
	{
		scanf("%d", &arr[i]);
		sort[i] = arr[i];
	}
    qsort(sort, sizeof(int), n, cmp);
	m = 1;
	for (int i=2; i<=n; ++i)
	{
		if (sort[m] != sort[i])
		{
			m = m + 1;
			sort[m] = sort[i];
		}
	}
	for (int i=1; i<=n; ++i)
		arr[i] = rank(arr[i]);
	
	
	int ans = 0;
	for (int i=1; i<=n; ++i)
	{
		ans = ans + sum(tree2, arr[i] - 1);
		add(tree1, arr[i], 1);
		add(tree2, arr[i], sum(tree2, arr[i] - 1));
	}	
	printf("%d", ans);
}

题目三

我们建立一个结构

用于存储以下标 i 为结尾的子序列的最大长度和个数

# include <stdio.h>

struct node
{
	int len; //长度 
	int num; //个数 
};

//不是该结构数组，是该结构体的树状数组
//用于维护一个范围的最大长度和个数
struct node tree[100];

int arr[100];
int sort[100];

int n, m;

//查询结尾数值<=i的所有递增子序列中
//长度最大的递增子序列长度是多少，赋值给maxlen和maxnum
int maxlen, maxnum;

int lowbit(int x)
{
	return x & (-x);
}

//以 i 这个值结尾的最长递增子序列达到了len长度
//并且这样的最长递增子序列的数量达到了cnt个
void add(int i, int l, int cnt)
{
	while (i <= m)
	{
		if (tree[i].len == l)
			tree[i].num = tree[i].num + cnt;
		else if (tree[i].len < l)
		{
			tree[i].len = l;
			tree[i].num = cnt;
		}
		i = i + lowbit(i);
	}
}

//结尾数值 <= i 的情况下，最长递增子序列的长度和个数为多少
void query(int x)
{
	maxlen = 0;
	maxnum = 0;
	while (x > 0)
	{
		if (tree[x].len == maxlen)
			maxnum = tree[x].num + maxnum;
		else if (tree[x].len > maxlen)
		{
			maxlen = tree[x].len;
			maxnum = tree[x].num;
		}
		x = x - lowbit(x);
	}
}

int rank(int x)
{
	int l = 1;
	int r = m;
	int mid;
	int ans;
	while (l <= r)
	{
		mid = (l+r) / 2;
		if (sort[mid] >= x)
		{
			r = mid - 1;
			ans = mid;
		}
		else
			l = mid + 1;
	}
	return ans;
}

int main()
{
	scanf("%d", &n);
	for (int i=1; i<=n; ++i)
	{
		scanf("%d", &arr[i]);
		sort[i] = arr[i];
	}
	qsort(sort, sizeof(sort), n, cmp);
	int m = 1;
	for (int i=2; i<=n; ++i)
	{
		if (sort[m] != sort[i])
		{
			sort[m] = sort[i];
			m = m + 1;
		}
	}
	memset(tree, 0, sizeof(tree));
	int y;
	for (int i=1; i<=m; ++i)
	{
		y = rank(arr[i]);
		query(y-1);
		add(y, maxlen+1, max(1, maxnum));
	}
	int ans = query(m);
	printf("%d", ans);
}

题目四

本题转化是非常巧妙的

我们首先需要对查询进行排序

按照 r 的大小进行排序

如图：

一个虚拟数组cnt[]（之所以说它是虚拟数组，因为可以用树状数组实现想要的操作，不需要真的定义这么一个数组）。

map[i] 记录 i 位置上的数上一次出现的位置

当遍历到原数组的下标 i 时，cnt[i]+1,如果 i 位的这个数之前出现过，即存在map[i]，则将cnt[map[i]]-1（在遍历到i之前已经遍历过last[i]位置了，因此cnt[map[i]]=1，所以这样操作下来，cnt[map[i]]=0)，不会对当前要求的结果造成影响

比如序列：2，3，4，3，4，2

当右边界为5时（下标从1开始），对应的cnt[]值分别为：1，0，0，1，1

所以区间【1，5】内不同的数字个数=3，区间【2，5】内不同的数字个数=2，区间【4，5】内不同的数字个数=2（树状数组累加和求解）

因为右边界一定，所以我们必须要确保选择的1是尽可能靠近右边界，确保答案正确

# include <stdio.h>
# include <string.h>
struct node
{
	int l;
	int r;
	int k;
};

int arr[100];

struct node query[100];

int ans[100];

int map[100];

int tree[100];

int n, m;

int compare(const void*a, const void* b)
{
	struct node* p1 = (struct node*)a;
	struct node* p2 = (struct node*)b;
	return *p1.r - *p2.r;
}

int lowbit(int x)
{
	return x & (-x);
}

void add(int i, int v)
{
	while (i <= n)
	{
		tree[i] = tree[i] + v;
		i = i + lowbit(i);
	}
}

int q(int x)
{
	int ans = 0;
	while (x > 0)
	{
		ans = tree[x] + ans;
		x = x - lowbit(x);
	}
	return ans;
}

int range(int l, int r)
{
	return sum(r) - sum(l-1);
}

void cmp(void)
{
	 qsort(query, sizeof(struct node), m, compare);
	 int q = 1; //遍历询问 
	 int l;
	 int r;
	 int k; 
	 for (int q=1; q <= m; ++i)
	 {
	 	r = query[q].r;
	 	for (; s<=r; ++s)
	 	{
	 		int color = arr[s];
	 		if (map[color] != 0)
	 			add(map[color], -1)
	 		add[s, 1];
	 		map[color] = s;
		}
		l = query[q].l;
		k = query[q].k;
		ans[i] = range(l, r);
	 }
}

int main()
{
	scanf("%d", &n);
	for (int i=1; i<=n; ++i)
	{
		scanf("%d", &arr[i]);
	}
	scanf("%d", &m);
	for (int i=1; i<=m; ++i)
	{
		scanf("%d %d", &query[i].l, &query[i].r);
		query[i].k = i;
	}
	
	cmp();
	for (int i=1; i<=m; ++i)
		printf("%d", ans[i]);
}