0.开源代码地址
官方实现:state-spaces/mamba (github.com)
最简化实现:johnma2006/mamba-minimal: Simple, minimal implementation of the Mamba SSM in one file of PyTorch. (github.com)
直接实现:alxndrTL/mamba.py: A simple and efficient Mamba implementation in PyTorch and MLX. (github.com)
官方代码做了大量优化,目录层级较多,对于理解模型含义较难,这里老师对上面第二最简化实现的代码进行了详细注释,该代码性能比官方实现差,但是对于理解模型原理比较直白。
这段代码的主要组成部分包括模型参数类ModelArgs、完整的Mamba模型类Mamba、残差块类ResidualBlock、单个Mamba块类MambaBlock、RMSNorm归一化类以及一些辅助函数。
1算法核心
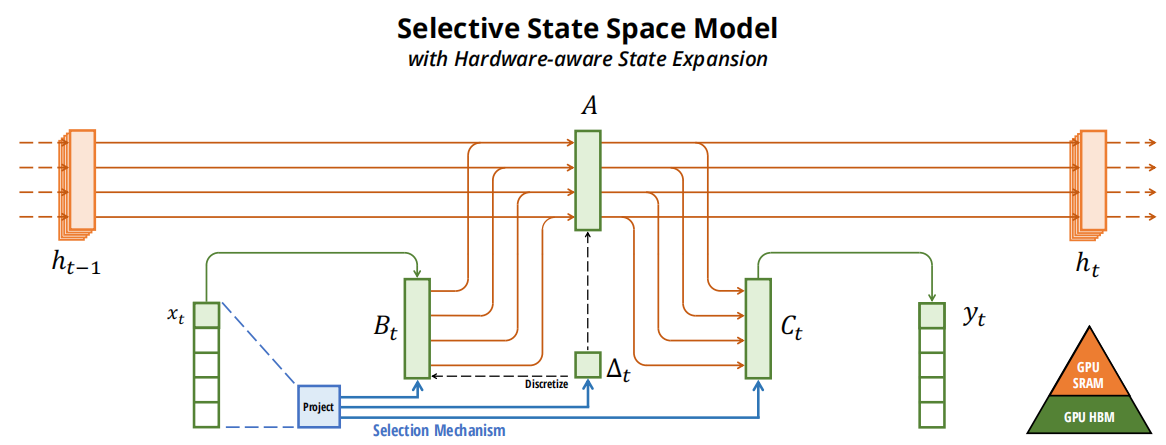
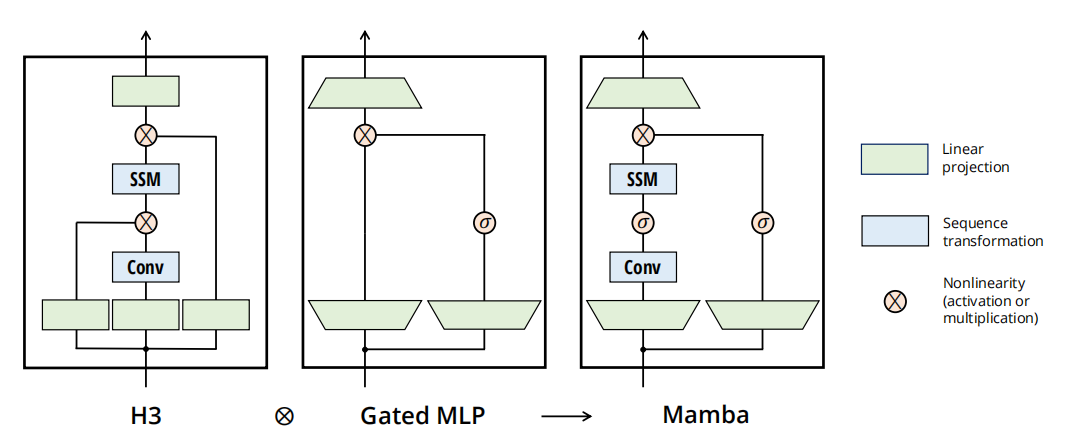
的算法图,原始论文中给出的Mamba(SSSM:Selective state Space model of )的前身S4(SSM:Structured State Space Model):

S6模块
S6模块是Mamba架构中的一个复杂组件,负责通过一系列线性变换和离散化过程处理输入序列。它在捕获序列的时间动态方面起着关键作用,这是序列建模任务(如语言建模)的一个关键方面。这里包括张量运算和自定义离散化方法来处理序列数据的复杂需求。
离散化def discretization(self)中有两行代码提出来解释,论文中离散化采用零阶保持:
A ‾ = e x p ( Δ A ) \overline{A}=exp(\Delta A) A=exp(ΔA) :对应代码中的self.dA
B ‾ = ( Δ A ) − 1 ( exp ( Δ A ) − I ) ⋅ Δ B \overline{B}=(\Delta A)^{-1}(\exp(\Delta A)-I)\cdot\Delta B B=(ΔA)−1(exp(ΔA)−I)⋅ΔB::对应代码中的self.dB
各个张量维度如下:

2.Mamba模型定义
2.1 ModelArgs 类
ModelArgs 类是用于存储和处理Mamba模型配置参数的容器。它使用Python的dataclass装饰器来自动生成初始化方法和类的字符串表示方法,简化了代码的编写。这个类中的每个属性对应于构建Mamba模型所需的一个配置参数,例如模型的隐藏层维度、层数、词汇表大小等。__post_init__方法在初始化后自动调用,用于执行一些额外的设置,比如计算内部维度d_inner和自动调整词汇表大小,以确保模型的配置参数是有效的和一致的。
# 使用dataclass装饰器自动生成初始化方法和类的字符串表示方法
@dataclass
class ModelArgs:
# @dataclass 会自动为这个类生成初始化方法和代表类的字符串形式的方法
d_model: int # 定义模型的隐藏层维度
n_layer: int # 定义模型的层数
vocab_size: int # 定义词汇表的大小
d_state: int = 16 # 定义状态空间的维度,默认为16
expand: int = 2 # 定义扩展因子,默认为2
dt_rank: Union[int, str] = 'auto' # 定义输入依赖步长Δ的秩,'auto'表示自动设置
d_conv: int = 4 # 定义卷积核的维度,默认为4
pad_vocab_size_multiple: int = 8 # 定义词汇表大小的最小公倍数,默认为8
conv_bias: bool = True # 定义卷积层是否使用偏置项
bias: bool = False # 定义其他层(如线性层)是否使用偏置项
def __post_init__(self):
# 在__init__后自动被调用,用于执行初始化之后的额外设置或验证
# 计算内部维度,即扩展后的维度
self.d_inner = int(self.expand * self.d_model)
if self.dt_rank == 'auto':# 如果dt_rank未指定,则自动计算设置
# 根据隐藏层维度自动计算Δ的秩
self.dt_rank = math.ceil(self.d_model / 16)
# 确保vocab_size是pad_vocab_size_multiple的倍数
# 如果不是,调整为最近的倍数
if self.vocab_size % self.pad_vocab_size_multiple != 0:
self.vocab_size += (self.pad_vocab_size_multiple
- self.vocab_size % self.pad_vocab_size_multiple)
2.2 Mamba 类
Mamba 类是Mamba模型的主干,继承自PyTorch的nn.Module类。这个类的实例化对象将构成整个Mamba模型的结构和前向传播逻辑。
在初始化方法__init__中,首先调用父类的构造函数来初始化模型。然后,根据传入的ModelArgs对象中的参数配置模型的各个组件:
self.embedding是一个嵌入层,它将输入的词汇ID转换为对应的向量表示。这些向量随后会被送入模型的深层网络中。self.layers是一个模块列表,其中包含了多个ResidualBlock残差块。这些残差块有助于训练深层网络并防止梯度消失问题。self.norm_f是一个RMSNorm归一化模块,用于在模型的某些层之后进行归一化操作,以稳定训练过程。self.lm_head是一个线性层,它将模型的最终隐藏状态映射回词汇表的大小,以便进行下一步的预测或分类任务。
在forward方法中,定义了模型的前向传播逻辑。输入input_ids首先通过嵌入层转换为向量表示,然后依次通过每个残差块进行处理。经过所有层之后,模型的输出通过RMSNorm归一化,最后通过线性层self.lm_head得到最终的logits输出。这个输出可以用于后续的损失计算或生成任务。
class Mamba(nn.Module):
def __init__(self, args: ModelArgs):
"""Full Mamba model."""
super().__init__()
# 保存传入的ModelArgs对象,包含模型的配置参数
self.args = args
# 创建一个嵌入层,将词汇表中的词转换为对应的向量表示
self.embedding = nn.Embedding(args.vocab_size, args.d_model)
# 创建一个包含多个残差块的模块列表,残差块的数量等于模型层数
self.layers = nn.ModuleList([ResidualBlock(args) for _ in range(args.n_layer)])
# 创建一个RMSNorm模块,用于归一化操作
self.norm_f = RMSNorm(args.d_model)
# 创建一个线性层,用于最终的输出,将隐藏层的输出映射回词汇表的大小
self.lm_head = nn.Linear(args.d_model, args.vocab_size, bias=False)
# 将线性层的输出权重与嵌入层的权重绑定,这是权重共享的一种形式,有助于减少参数数量并可能提高模型的泛化能力
self.lm_head.weight = self.embedding.weight # Tie output projection to embedding weights.
# See "Weight Tying" paper
def forward(self, input_ids):
"""
Args:
input_ids (long tensor): shape (b, l) (See Glossary at top for definitions of b, l, d_in, n...)
Returns:
logits: shape (b, l, vocab_size)
Official Implementation:
class MambaLMHeadModel, https://github.com/state-spaces/mamba/blob/main/mamba_ssm/models/mixer_seq_simple.py#L173
"""
# 将输入ID转换为向量表示
x = self.embedding(input_ids)
# 遍历所有的残差块,并应用它们
for layer in self.layers:
x = layer(x)
# 应用归一化操作
x = self.norm_f(x)
# 通过线性层得到最终的logits输出
logits = self.lm_head(x)
# 返回模型的输出
return logits
解释一下:为什么输入的input_ids已经是经过分词器(tokenizer)处理后的词汇表索引,还需要通过nn.Embedding?
这些索引代表了输入文本中的单词或子词单元在词汇表中的位置。尽管这些索引已经是一个相对紧凑的数值表示,但它们并不直接对应于模型可以处理的向量表示。
nn.Embedding层的作用是将这些离散的索引映射到一个连续的向量空间中。每个索引input_ids中的值都会被nn.Embedding层转换成一个固定维度的向量,这个向量捕捉了对应单词或子词的语义信息。这个转换过程是模型学习的一部分,通过训练数据中的模式,模型可以学习到如何将这些索引映射到能够有效表示输入文本的向量。
2.3 ResidualBlock 类
定义了Mamba模型中的一个残差块。这个类的目的是为了在模型中引入残差连接,这有助于训练深层网络,因为它允许梯度直接流过网络,从而缓解了梯度消失问题。
在__init__方法中,首先调用父类nn.Module的构造函数来初始化残差块。然后,根据传入的ModelArgs对象中的参数配置残差块的组件:
self.mixer是一个MambaBlock实例,它是这个残差块的核心组件,负责执行Mamba模型的大部分计算。self.norm是一个RMSNorm归一化模块,用于在将数据送入MambaBlock之前进行归一化处理。
在forward方法中,定义了残差块的前向传播逻辑。输入张量x首先通过RMSNorm模块进行归一化,然后送入MambaBlock。MambaBlock的输出接着与原始输入x相加,形成残差连接。这样做可以使得模型的学习更加灵活,因为它允许模型学习到输入和输出之间的恒等映射(即不改变输入数据),这在某些情况下是有益的。最后,残差块的输出被返回。
class ResidualBlock(nn.Module):
def __init__(self, args: ModelArgs):
"""Simple block wrapping Mamba block with normalization and residual connection."""
super().__init__()
# 保存传入的ModelArgs对象,包含模型的配置参数
self.args = args
# 创建一个MambaBlock,它是这个残差块的核心组件
self.mixer = MambaBlock(args)
# 创建一个RMSNorm归一化模块,用于归一化操作
self.norm = RMSNorm(args.d_model)
def forward(self, x):
"""
Args:
x: shape (b, l, d) (See Glossary at top for definitions of b, l, d_in, n...)
x (Tensor): 输入张量,形状为(batch_size, sequence_length, hidden_size)
Returns:
output: shape (b, l, d)
输出张量,形状与输入相同
Official Implementation:
Block.forward(), https://github.com/state-spaces/mamba/blob/main/mamba_ssm/modules/mamba_simple.py#L297
Note: the official repo chains residual blocks that look like
[Add -> Norm -> Mamba] -> [Add -> Norm -> Mamba] -> [Add -> Norm -> Mamba] -> ...
where the first Add is a no-op. This is purely for performance reasons as this
allows them to fuse the Add->Norm.
We instead implement our blocks as the more familiar, simpler, and numerically equivalent
[Norm -> Mamba -> Add] -> [Norm -> Mamba -> Add] -> [Norm -> Mamba -> Add] -> ....
"""
# 应用归一化和MambaBlock,然后与输入x进行残差连接
output = self.mixer(self.norm(x)) + x
return output
2.4 MambaBlock 类
MambaBlock 类定义了Mamba模型中的一个基本构建块,即Mamba块。这个块是模型的核心组件,负责执行序列数据的处理和状态空间模型的更新。
在__init__方法中,首先调用父类nn.Module的构造函数来初始化Mamba块。然后,根据传入的ModelArgs对象中的参数配置Mamba块的组件:
self.in_proj是一个线性变换层,用于输入的投影。self.conv1d是一个一维卷积层,用于执行深度卷积,这是Mamba模型的特色之一,用于处理序列数据。self.x_proj和self.dt_proj是线性变换层,用于将输入映射到状态空间模型的参数。self.A_log是矩阵A的对数值,作为一个可训练参数。self.D是矩阵D,初始化为全1,也是一个可训练参数。self.out_proj是一个线性变换层,用于输出的投影。
在forward方法中,定义了Mamba块的前向传播逻辑。输入张量x首先通过线性变换层和深度卷积层进行处理,然后应用激活函数。接着,通过状态空间模型(ssm)和选择性扫描(selective_scan)算法更新状态,并计算输出。最后,输出通过另一个线性变换层进行投影,得到最终的输出结果。
ssm方法负责运行状态空间模型,它使用矩阵A、B、C和D以及输入x来更新状态并计算输出。
selective_scan方法执行选择性扫描算法,这是Mamba模型的关键特性,它允许模型根据输入动态调整其行为,从而更好地处理序列数据。通过这种方式,Mamba模型能够有效地捕捉序列中的长期依赖关系,同时保持线性时间复杂度。

class MambaBlock(nn.Module):
def __init__(self, args: ModelArgs):
"""A single Mamba block, as described in Figure 3 in Section 3.4 in the Mamba paper [1]."""
super().__init__()
# 保存模型参数
self.args = args
# 输入线性变换层
self.in_proj = nn.Linear(args.d_model, args.d_inner * 2, bias=args.bias)
# 创建了一个所谓的“深度卷积”,其中每个输入通道被单独卷积到每个输出通道。
# 这意味着每个输出通道的结果是通过仅与一个输入通道卷积得到的。
self.conv1d = nn.Conv1d(
in_channels=args.d_inner,
out_channels=args.d_inner,
bias=args.conv_bias,
kernel_size=args.d_conv,
groups=args.d_inner,
padding=args.d_conv - 1,
)
# x_proj takes in `x` and outputs the input-specific Δ, B, C
# 将输入x映射到状态空间模型的参数Δ、B和C
self.x_proj = nn.Linear(args.d_inner, args.dt_rank + args.d_state * 2, bias=False)
# dt_proj projects Δ from dt_rank to d_in
# 将Δ从args.dt_rank维度映射到args.d_inner维度
self.dt_proj = nn.Linear(args.dt_rank, args.d_inner, bias=True)
# 创建一个重复的序列,用于初始化状态空间模型的矩阵A
# n->dxn
A = repeat(torch.arange(1, args.d_state + 1), 'n -> d n', d=args.d_inner)
# 将矩阵A的对数值作为可训练参数保存
self.A_log = nn.Parameter(torch.log(A))
# 初始化矩阵D为全1的可训练参数
self.D = nn.Parameter(torch.ones(args.d_inner))
# 输出线性变换层
self.out_proj = nn.Linear(args.d_inner, args.d_model, bias=args.bias)
def forward(self, x):
"""MambaBlock的前向传播函数,与Mamba论文图3 Section 3.4相同.
Args:
x: shape (b, l, d) (See Glossary at top for definitions of b, l, d_in, n...)
Returns:
output: shape (b, l, d)
Official Implementation:
class Mamba, https://github.com/state-spaces/mamba/blob/main/mamba_ssm/modules/mamba_simple.py#L119
mamba_inner_ref(), https://github.com/state-spaces/mamba/blob/main/mamba_ssm/ops/selective_scan_interface.py#L311
"""
# 获取输入x的维度
# batchsize,seq_len,dim
(b, l, d) = x.shape # 获取输入x的维度
# 应用输入线性变换
x_and_res = self.in_proj(x) # shape (b, l, 2 * d_in)
# 将变换后的输出分为两部分x和res。
# 得到的x分为两个部分,一部分x继续用于后续变换,生成所需要的参数,res用于残差部分
(x, res) = x_and_res.split(split_size=[self.args.d_inner, self.args.d_inner], dim=-1)
# 调整x的形状
x = rearrange(x, 'b l d_in -> b d_in l')
# 应用深度卷积,然后截取前l个输出
x = self.conv1d(x)[:, :, :l]
# 再次调整x的形状
x = rearrange(x, 'b d_in l -> b l d_in')
# 应用SiLU激活函数
x = F.silu(x)
# 运行状态空间模型
y = self.ssm(x)
# 将res的SiLU激活结果与y相乘
y = y * F.silu(res)
# 应用输出线性变换
output = self.out_proj(y)
# 返回输出结果
return output
def ssm(self, x):
"""运行状态空间模型,参考Mamba论文 Section 3.2和注释[2]:
- Algorithm 2 in Section 3.2 in the Mamba paper [1]
- run_SSM(A, B, C, u) in The Annotated S4 [2]
Args:
x: shape (b, l, d_in) (See Glossary at top for definitions of b, l, d_in, n...)
Returns:
output: shape (b, l, d_in)
Official Implementation:
mamba_inner_ref(), https://github.com/state-spaces/mamba/blob/main/mamba_ssm/ops/selective_scan_interface.py#L311
"""
# 获取A_log的维度
# A在初始化时候经过如下赋值:
# A = repeat(torch.arange(1, args.d_state + 1), 'n -> d n', d=args.d_inner)
# self.A_log = nn.Parameter(torch.log(A))
# (args.d_inner, args.d_state)
(d_in, n) = self.A_log.shape # 获取A_log的维度
# 计算 ∆ A B C D, 这些属于状态空间参数.
# A, D 是 与输入无关的 (见Mamba论文Section 3.5.2 "Interpretation of A" for why A isn't selective)
# ∆, B, C 与输入有关(这是与线性是不变模型S4最大的不同,
# 也是为什么Mamba被称为 “选择性” 状态空间的原因)
# 计算矩阵A
A = -torch.exp(self.A_log.float()) # shape (d_in, n)
# 取D的值
D = self.D.float()
# 应用x的投影变换
# ( b,l,d_in) -> (b, l, dt_rank + 2*n)
x_dbl = self.x_proj(x) # (b, l, dt_rank + 2*n)
# 分割delta, B, C
# delta: (b, l, dt_rank). B, C: (b, l, n)
(delta, B, C) = x_dbl.split(split_size=[self.args.dt_rank, n, n], dim=-1)
# 应用dt_proj并计算delta
delta = F.softplus(self.dt_proj(delta)) # (b, l, d_in)
# 应用选择性扫描算法
y = self.selective_scan(x, delta, A, B, C, D)
return y
def selective_scan(self, u, delta, A, B, C, D):
"""执行选择性扫描算法,参考Mamba论文[1] Section 2和注释[2]. See:
- Section 2 State Space Models in the Mamba paper [1]
- Algorithm 2 in Section 3.2 in the Mamba paper [1]
- run_SSM(A, B, C, u) in The Annotated S4 [2]
经典的离散状态空间公式:
x(t + 1) = Ax(t) + Bu(t)
y(t) = Cx(t) + Du(t)
除了B和C (以及step size delta用于离散化) 与输入x(t)相关.
参数:
u: shape (b, l, d_in)
delta: shape (b, l, d_in)
A: shape (d_in, n)
B: shape (b, l, n)
C: shape (b, l, n)
D: shape (d_in,)
过程概述:
Returns:
output: shape (b, l, d_in)
Official Implementation:
selective_scan_ref(), https://github.com/state-spaces/mamba/blob/main/mamba_ssm/ops/selective_scan_interface.py#L86
Note: I refactored some parts out of `selective_scan_ref` out, so the functionality doesn't match exactly.
"""
# 获取输入u的维度
(b, l, d_in) = u.shape
# 获取矩阵A的列数
n = A.shape[1] # A: shape (d_in, n)
# 离散化连续参数(A, B)
# - A 使用 zero-order hold (ZOH) 离散化 (see Section 2 Equation 4 in the Mamba paper [1])
# - B is 使用一个简化的Euler discretization而不是ZOH.根据作者的讨论:
# "A is the more important term and the performance doesn't change much with the simplification on B"
# 计算离散化的A
# 将delta和A进行点乘,将A沿着delta的最后一个维度进行广播,然后执行逐元素乘法
# A:(d_in, n),delta:(b, l, d_in)
# A广播拓展->(b,l,d_in, n),deltaA对应原论文中的A_bar
deltaA = torch.exp(einsum(delta, A, 'b l d_in, d_in n -> b l d_in n'))
# delta、B和u,这个计算和原始论文不同
deltaB_u = einsum(delta, B, u, 'b l d_in, b l n, b l d_in -> b l d_in n')
# Perform selective scan (see scan_SSM() in The Annotated S4 [2])
# Note that the below is sequential, while the official implementation does a much faster parallel scan that
# is additionally hardware-aware (like FlashAttention).
# 执行选择性扫描,初始化状态x为零
x = torch.zeros((b, d_in, n), device=deltaA.device)
# 初始化输出列表ys
ys = []
for i in range(l):
# 更新状态x
# deltaA:((b,l,d_in, n)
# deltaB_u:( b,l,d_in,n)
# x:
x = deltaA[:, i] * x + deltaB_u[:, i]
# 计算输出y
y = einsum(x, C[:, i, :], 'b d_in n, b n -> b d_in')
# 将输出y添加到列表ys中
ys.append(y)
# 将列表ys堆叠成张量y
y = torch.stack(ys, dim=1) # shape (b, l, d_in)
# 将输入u乘以D并加到输出y上
y = y + u * D
return y
解释1:深度卷积的几行代码
x = rearrange(x, ‘b l d_in -> b d_in l’) 调整x的形状
这行代码使用
rearrange函数将输入张量x的形状从(batch_size, sequence_length, d_model)转换为(batch_size, d_model, sequence_length)。这种形状调整是为了适配后续的一维卷积层self.conv1d,该卷积层期望输入的形状为(batch_size, channels, length),其中channels是卷积核的深度,length是序列的长度。x = self.conv1d(x)[:, :, :l] 应用深度卷积
self.conv1d是一个一维卷积层,它沿着序列长度l的方向应用卷积核。由于self.conv1d的in_channels参数设置为args.d_inner,这意味着卷积操作是在d_model维的特征空间内独立进行的。卷积操作的输出是一个三维张量,其形状为(batch_size, d_inner, sequence_length)。然后,代码通过切片操作[:, :, :l]只保留了序列长度为l的输出,这是因为我们只对序列中的前l个元素感兴趣。x = rearrange(x, ‘b d_in l -> b l d_in’ 再次调整x的形状
最后,为了继续后续的计算,需要将卷积后的张量形状再次调整回
(batch_size, sequence_length, d_model)。这样做是为了确保数据在后续层中的流动是连贯的,特别是当数据传递给后续的Mamba块或其他层时。这里的rearrange函数将卷积输出的形状从(batch_size, d_inner, sequence_length)转换回(batch_size, sequence_length, d_inner)
解释2:A = -torch.exp(self.A_log.float())前面的负号
这里的负号
-是因为在状态空间模型中,矩阵A通常表示的是一个离散时间系统的转换矩阵,它描述了系统状态随时间的演变。在许多情况下,A矩阵的元素应该是负的,以确保系统的稳定性。这是因为在离散时间系统中,我们希望系统的状态随着时间的推移而衰减或稳定下来,而不是增长,从而避免系统变得不稳定或发散。
解释3:状态空间更新代码
这两行代码首先根据当前时间步的转换矩阵
deltaA和输入影响deltaB_u更新状态向量x,然后计算状态向量x和输出矩阵C的点乘,得到当前时间步的输出y。这个过程是状态空间模型中的核心计算步骤,它允许模型动态地处理序列数据并生成响应。
x = deltaA[:, i] * x + deltaB_u[:, i]
deltaA是一个四维张量,其形状为(batch_size, sequence_length, d_in, n)。这里deltaA[:, i]表示我们选择了deltaA张量中第i个时间步的切片,形状变为(batch_size, d_in, n)。x是状态向量,其形状为(batch_size, d_in, n),代表当前时间步的状态。deltaB_u是一个四维张量,其形状也为(batch_size, sequence_length, d_in, n),它是通过delta、B和输入u计算得到的,代表了输入对状态的直接影响。- 这行代码首先执行
deltaA[:, i] * x,这是一个逐元素乘法操作,它根据当前时间步的转换矩阵更新状态向量x。由于deltaA[:, i]的形状是(batch_size, d_in, n),它可以直接与形状相同的x进行逐元素乘法。- 接着,代码执行
+ deltaB_u[:, i],将输入的影响加到更新后的状态向量x上。这里的deltaB_u[:, i]是deltaB_u张量中第i个时间步的切片,形状也是(batch_size, d_in, n)。y = einsum(x, C[:, i, :], 'b d_in n, b n -> b d_in')
- 这行代码使用
einsum函数来计算输出y。einsum是PyTorch中的一个函数,用于执行复杂的张量运算。x是当前状态向量,形状为(batch_size, d_in, n)。C[:, i, :]是从输出参数矩阵C中取出的第i个时间步的切片,形状为(batch_size, n, d_in)。'b d_in n, b n -> b d_in'是einsum的索引模式,它指示了如何执行点乘和求和操作。在这个模式中,'b'表示批次维度保持不变,'d_in n'表示x的第二个和第三个维度与C的第二个维度进行点乘,'b d_in'表示输出y的形状应该与x的前两个维度相同。- 结果
y的形状是(batch_size, d_in),它是模型在当前时间步对输入序列的响应。
2.5 RMSNorm 类
这个类实现了基于均方根的归一化操作。它接收输入x,计算其均方根值,并使用这个值来归一化输入。这种归一化有助于模型的训练稳定性。
class RMSNorm(nn.Module):
def __init__(self, d_model: int, eps: float = 1e-5):
"""
初始化RMSNorm模块,该模块实现了基于均方根的归一化操作。
参数:
d_model (int): 模型的特征维度。
eps (float, 可选): 为了避免除以零,添加到分母中的一个小的常数。
"""
super().__init__()
self.eps = eps # 保存输入的eps值,用于数值稳定性
self.weight = nn.Parameter(torch.ones(d_model)) # 创建一个可训练的权重参数,初始值为全1,维度与输入特征维度d_model相同
def forward(self, x):
"""
定义RMSNorm模块的前向传播函数。
参数:
x (Tensor): 输入的张量,通常是一个特征矩阵,其形状为(batch_size, sequence_length, d_model)。
返回:
output (Tensor): 归一化后的特征矩阵。
"""
output = x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps) * self.weight # 计算归一化输出
return output # 返回归一化后的输出
小结:状态空间参数是如何与输入相关的
这个是S6与S4的根本区别
在上面的MambaBlock类的代码中,状态空间的参数与输入相关性体现在self.x_proj和self.dt_proj的使用上,以及在ssm和selective_scan方法中的计算过程中。
self.x_proj和self.dt_proj:self.x_proj是一个线性变换层,它将输入x映射到状态空间模型的参数Δ、B和C。这个映射是输入依赖的,因为x是模型的输入,它的值会直接影响到这些参数的计算。self.dt_proj是一个线性变换层,用于将Δ从args.dt_rank维度映射到args.d_inner维度。虽然这个映射本身是一个固定的线性变换,但它的输入(即x)是依赖于输入数据的。
ssm方法:- 在
ssm方法中,计算了状态空间模型的参数A、B、C和D。其中,A和D是与输入无关的,而B和C是通过self.x_proj和self.dt_proj从输入x中计算得到的,因此它们与输入是相关的。
- 在
selective_scan方法:selective_scan方法执行选择性扫描算法,它是状态空间模型的核心计算过程。在这个方法中,输入u(实际上是x经过一系列变换后的结果)与状态空间参数Δ、A、B、C和D一起使用,来更新状态并计算输出。- 方法中的
deltaA和deltaB_u计算显示了输入u如何影响状态空间参数。deltaA是通过einsum函数将输入u的每个元素与矩阵A的每个元素进行点乘得到的,这意味着输入的每个元素都会影响A的每个元素。 deltaB_u是通过einsum函数将输入u、矩阵B和Δ进行三元组乘法得到的,这进一步表明输入u直接影响了状态空间参数B的计算。
总的来说,状态空间的参数与输入相关性是通过输入数据x直接影响Δ、B和C的计算来实现的。这种相关性使得Mamba模型能够根据输入数据的不同动态调整其内部状态,从而更好地捕捉序列数据的特性。这是Mamba模型区别于传统的线性时不变(LTI)状态空间模型的关键特性。
3.模型测试代码
3.1 加载模型
from model import Mamba, ModelArgs
from transformers import AutoTokenizer
# One of:
# 'state-spaces/mamba-2.8b-slimpj'
# 'state-spaces/mamba-2.8b'
# 'state-spaces/mamba-1.4b'
# 'state-spaces/mamba-790m'
# 'state-spaces/mamba-370m'
# 'state-spaces/mamba-130m'
pretrained_model_name = 'state-spaces/mamba-370m'
model = Mamba.from_pretrained(pretrained_model_name)
tokenizer = AutoTokenizer.from_pretrained('EleutherAI/gpt-neox-20b')
3.2 生成文本
这个函数通过迭代地向模型提供输入,并基于模型预测的概率分布来生成下一个令牌,直到达到指定的令牌数量。生成过程中,可以通过top_k采样来限制概率分布,或者通过采样来随机选择令牌,从而增加生成文本的多样性。最终,函数返回生成的文本
import torch
import torch.nn.functional as F
def generate(model,
tokenizer,
prompt: str,
n_tokens_to_gen: int = 50,
sample: bool = True,
top_k: int = 40):
# 将模型设置为评估模式,这通常会关闭dropout等训练时的特性。
model.eval()
# 使用分词器将提示字符串转换为模型可以处理的输入ID。
input_ids = tokenizer(prompt, return_tensors='pt').input_ids
# 循环生成指定数量的令牌。
for token_n in range(n_tokens_to_gen):
# 无需计算梯度,因为我们是在生成文本而不是训练模型。
with torch.no_grad():
# 准备输入模型的索引。
indices_to_input = input_ids
# 通过模型获取当前输入的下一个令牌的logits。
next_token_logits = model(indices_to_input)[:, -1]
# 对logits应用softmax函数,将其转换为概率分布。
probs = F.softmax(next_token_logits, dim=-1)
# 获取概率分布的形状,即批次大小和词汇表大小。
(batch, vocab_size) = probs.shape
# 如果指定了top_k采样,则获取概率最高的k个令牌及其对应的值和索引。
if top_k is not None:
(values, indices) = torch.topk(probs, k=top_k)
# 将概率低于最低top_k令牌的概率值设置为0。
probs[probs < values[:, -1, None]] = 0
# 重新归一化概率分布,使得所有概率之和为1。
probs = probs / probs.sum(axis=1, keepdims=True)
# 如果采样为True,则通过多项式采样(Multinomial Sampling)来选择下一个令牌。
if sample:
next_indices = torch.multinomial(probs, num_samples=1)
else:# 如果不采样,则选择概率最高的令牌作为下一个令牌。
next_indices = torch.argmax(probs, dim=-1)[:, None]
# 将生成的下一个令牌添加到输入ID列表中。
input_ids = torch.cat([input_ids, next_indices], dim=1)
# 将最终的输入ID转换为文本,并解码为可读的字符串。
output_completions = [tokenizer.decode(output.tolist()) for output in input_ids][0]
# 返回生成的文本。
return output_completions
print(generate(model, tokenizer, 'Mamba is the'))
Mamba is the world’s longest venomous snake with an estimated length of over 150 m. With such a large size and a venomous bite, Mamba kills by stabbing the victim (which is more painful and less effective than a single stab of the bite)
print(generate(model, tokenizer, 'John: Hi!\nSally:'))
John: Hi!
Sally: Hey!
John: So, when’s the wedding?
Sally: We haven’t decided.
John: It’s in September.
Sally: Yeah, we were thinking July or August.
附:完整模型代码
"""Simple, minimal implementation of Mamba in one file of PyTorch.
Suggest reading the following before/while reading the code:
[1] Mamba: Linear-Time Sequence Modeling with Selective State Spaces (Albert Gu and Tri Dao)
https://arxiv.org/abs/2312.00752
[2] The Annotated S4 (Sasha Rush and Sidd Karamcheti)
https://srush.github.io/annotated-s4
Glossary:
b: batch size (`B` in Mamba paper [1] Algorithm 2)
l: sequence length (`L` in [1] Algorithm 2)
d or d_model: hidden dim
n or d_state: latent state dim (`N` in [1] Algorithm 2)
expand: expansion factor (`E` in [1] Section 3.4)
d_in or d_inner: d * expand (`D` in [1] Algorithm 2)
A, B, C, D: state space parameters (See any state space representation formula)
(B, C are input-dependent (aka selective, a key innovation in Mamba); A, D are not)
Δ or delta: input-dependent step size
dt_rank: rank of Δ (See [1] Section 3.6 "Parameterization of ∆")
"""
from __future__ import annotations
import math
import json
import torch
import torch.nn as nn
import torch.nn.functional as F
from dataclasses import dataclass
from einops import rearrange, repeat, einsum
# 使用dataclass装饰器自动生成初始化方法和类的字符串表示方法
@dataclass
class ModelArgs:
# @dataclass 会自动为这个类生成初始化方法和代表类的字符串形式的方法
d_model: int # 定义模型的隐藏层维度
n_layer: int # 定义模型的层数
vocab_size: int # 定义词汇表的大小
d_state: int = 16 # 定义状态空间的维度,默认为16
expand: int = 2 # 定义扩展因子,默认为2
dt_rank: Union[int, str] = 'auto' # 定义输入依赖步长Δ的秩,'auto'表示自动设置
d_conv: int = 4 # 定义卷积核的维度,默认为4
pad_vocab_size_multiple: int = 8 # 定义词汇表大小的最小公倍数,默认为8
conv_bias: bool = True # 定义卷积层是否使用偏置项
bias: bool = False # 定义其他层(如线性层)是否使用偏置项
def __post_init__(self):
# 在__init__后自动被调用,用于执行初始化之后的额外设置或验证
# 计算内部维度,即扩展后的维度
self.d_inner = int(self.expand * self.d_model)
if self.dt_rank == 'auto':# 如果dt_rank未指定,则自动计算设置
# 根据隐藏层维度自动计算Δ的秩
self.dt_rank = math.ceil(self.d_model / 16)
# 确保vocab_size是pad_vocab_size_multiple的倍数
# 如果不是,调整为最近的倍数
if self.vocab_size % self.pad_vocab_size_multiple != 0:
self.vocab_size += (self.pad_vocab_size_multiple
- self.vocab_size % self.pad_vocab_size_multiple)
class Mamba(nn.Module):
def __init__(self, args: ModelArgs):
"""Full Mamba model."""
super().__init__()
# 保存传入的ModelArgs对象,包含模型的配置参数
self.args = args
# 创建一个嵌入层,将词汇表中的词转换为对应的向量表示
self.embedding = nn.Embedding(args.vocab_size, args.d_model)
# 创建一个包含多个残差块的模块列表,残差块的数量等于模型层数
self.layers = nn.ModuleList([ResidualBlock(args) for _ in range(args.n_layer)])
# 创建一个RMSNorm模块,用于归一化操作
self.norm_f = RMSNorm(args.d_model)
# 创建一个线性层,用于最终的输出,将隐藏层的输出映射回词汇表的大小
self.lm_head = nn.Linear(args.d_model, args.vocab_size, bias=False)
# 将线性层的输出权重与嵌入层的权重绑定,这是权重共享的一种形式,有助于减少参数数量并可能提高模型的泛化能力
self.lm_head.weight = self.embedding.weight # Tie output projection to embedding weights.
# See "Weight Tying" paper
def forward(self, input_ids):
"""
Args:
input_ids (long tensor): shape (b, l) (See Glossary at top for definitions of b, l, d_in, n...)
Returns:
logits: shape (b, l, vocab_size)
Official Implementation:
class MambaLMHeadModel, https://github.com/state-spaces/mamba/blob/main/mamba_ssm/models/mixer_seq_simple.py#L173
"""
# 将输入ID转换为向量表示
x = self.embedding(input_ids)
# 遍历所有的残差块,并应用它们
for layer in self.layers:
x = layer(x)
# 应用归一化操作
x = self.norm_f(x)
# 通过线性层得到最终的logits输出
logits = self.lm_head(x)
# 返回模型的输出
return logits
@staticmethod
def from_pretrained(pretrained_model_name: str):
"""Load pretrained weights from HuggingFace into model.
Args:
pretrained_model_name: One of
* 'state-spaces/mamba-2.8b-slimpj'
* 'state-spaces/mamba-2.8b'
* 'state-spaces/mamba-1.4b'
* 'state-spaces/mamba-790m'
* 'state-spaces/mamba-370m'
* 'state-spaces/mamba-130m'
Returns:
model: Mamba model with weights loaded
"""
from transformers.utils import WEIGHTS_NAME, CONFIG_NAME
from transformers.utils.hub import cached_file
def load_config_hf(model_name):
resolved_archive_file = cached_file(model_name, CONFIG_NAME,
_raise_exceptions_for_missing_entries=False)
return json.load(open(resolved_archive_file))
def load_state_dict_hf(model_name, device=None, dtype=None):
resolved_archive_file = cached_file(model_name, WEIGHTS_NAME,
_raise_exceptions_for_missing_entries=False)
return torch.load(resolved_archive_file, weights_only=True, map_location='cpu', mmap=True)
config_data = load_config_hf(pretrained_model_name)
args = ModelArgs(
d_model=config_data['d_model'],
n_layer=config_data['n_layer'],
vocab_size=config_data['vocab_size']
)
model = Mamba(args)
state_dict = load_state_dict_hf(pretrained_model_name)
new_state_dict = {}
for key in state_dict:
new_key = key.replace('backbone.', '')
new_state_dict[new_key] = state_dict[key]
model.load_state_dict(new_state_dict)
return model
class ResidualBlock(nn.Module):
def __init__(self, args: ModelArgs):
"""Simple block wrapping Mamba block with normalization and residual connection."""
super().__init__()
# 保存传入的ModelArgs对象,包含模型的配置参数
self.args = args
# 创建一个MambaBlock,它是这个残差块的核心组件
self.mixer = MambaBlock(args)
# 创建一个RMSNorm归一化模块,用于归一化操作
self.norm = RMSNorm(args.d_model)
def forward(self, x):
"""
Args:
x: shape (b, l, d) (See Glossary at top for definitions of b, l, d_in, n...)
x (Tensor): 输入张量,形状为(batch_size, sequence_length, hidden_size)
Returns:
output: shape (b, l, d)
输出张量,形状与输入相同
Official Implementation:
Block.forward(), https://github.com/state-spaces/mamba/blob/main/mamba_ssm/modules/mamba_simple.py#L297
Note: the official repo chains residual blocks that look like
[Add -> Norm -> Mamba] -> [Add -> Norm -> Mamba] -> [Add -> Norm -> Mamba] -> ...
where the first Add is a no-op. This is purely for performance reasons as this
allows them to fuse the Add->Norm.
We instead implement our blocks as the more familiar, simpler, and numerically equivalent
[Norm -> Mamba -> Add] -> [Norm -> Mamba -> Add] -> [Norm -> Mamba -> Add] -> ....
"""
# 应用归一化和MambaBlock,然后与输入x进行残差连接
output = self.mixer(self.norm(x)) + x
return output
class MambaBlock(nn.Module):
def __init__(self, args: ModelArgs):
"""A single Mamba block, as described in Figure 3 in Section 3.4 in the Mamba paper [1]."""
super().__init__()
# 保存模型参数
self.args = args
# 输入线性变换层
self.in_proj = nn.Linear(args.d_model, args.d_inner * 2, bias=args.bias)
# 创建了一个所谓的“深度卷积”,其中每个输入通道被单独卷积到每个输出通道。
# 这意味着每个输出通道的结果是通过仅与一个输入通道卷积得到的。
self.conv1d = nn.Conv1d(
in_channels=args.d_inner,
out_channels=args.d_inner,
bias=args.conv_bias,
kernel_size=args.d_conv,
groups=args.d_inner,
padding=args.d_conv - 1,
)
# x_proj takes in `x` and outputs the input-specific Δ, B, C
# 将输入x映射到状态空间模型的参数Δ、B和C
self.x_proj = nn.Linear(args.d_inner, args.dt_rank + args.d_state * 2, bias=False)
# dt_proj projects Δ from dt_rank to d_in
# 将Δ从args.dt_rank维度映射到args.d_inner维度
self.dt_proj = nn.Linear(args.dt_rank, args.d_inner, bias=True)
# 创建一个重复的序列,用于初始化状态空间模型的矩阵A
# n->dxn
A = repeat(torch.arange(1, args.d_state + 1), 'n -> d n', d=args.d_inner)
# 将矩阵A的对数值作为可训练参数保存
self.A_log = nn.Parameter(torch.log(A))
# 初始化矩阵D为全1的可训练参数
self.D = nn.Parameter(torch.ones(args.d_inner))
# 输出线性变换层
self.out_proj = nn.Linear(args.d_inner, args.d_model, bias=args.bias)
def forward(self, x):
"""MambaBlock的前向传播函数,与Mamba论文图3 Section 3.4相同.
Args:
x: shape (b, l, d) (See Glossary at top for definitions of b, l, d_in, n...)
Returns:
output: shape (b, l, d)
Official Implementation:
class Mamba, https://github.com/state-spaces/mamba/blob/main/mamba_ssm/modules/mamba_simple.py#L119
mamba_inner_ref(), https://github.com/state-spaces/mamba/blob/main/mamba_ssm/ops/selective_scan_interface.py#L311
"""
# 获取输入x的维度
# batchsize,seq_len,dim
(b, l, d) = x.shape # 获取输入x的维度
# 应用输入线性变换
x_and_res = self.in_proj(x) # shape (b, l, 2 * d_in)
# 将变换后的输出分为两部分x和res。
# 得到的x分为两个部分,一部分x继续用于后续变换,生成所需要的参数,res用于残差部分
(x, res) = x_and_res.split(split_size=[self.args.d_inner, self.args.d_inner], dim=-1)
# 调整x的形状
x = rearrange(x, 'b l d_in -> b d_in l')
# 应用深度卷积,然后截取前l个输出
x = self.conv1d(x)[:, :, :l]
# 再次调整x的形状
x = rearrange(x, 'b d_in l -> b l d_in')
# 应用SiLU激活函数
x = F.silu(x)
# 运行状态空间模型
y = self.ssm(x)
# 将res的SiLU激活结果与y相乘
y = y * F.silu(res)
# 应用输出线性变换
output = self.out_proj(y)
# 返回输出结果
return output
def ssm(self, x):
"""运行状态空间模型,参考Mamba论文 Section 3.2和注释[2]:
- Algorithm 2 in Section 3.2 in the Mamba paper [1]
- run_SSM(A, B, C, u) in The Annotated S4 [2]
Args:
x: shape (b, l, d_in) (See Glossary at top for definitions of b, l, d_in, n...)
Returns:
output: shape (b, l, d_in)
Official Implementation:
mamba_inner_ref(), https://github.com/state-spaces/mamba/blob/main/mamba_ssm/ops/selective_scan_interface.py#L311
"""
# 获取A_log的维度
# A在初始化时候经过如下赋值:
# A = repeat(torch.arange(1, args.d_state + 1), 'n -> d n', d=args.d_inner)
# self.A_log = nn.Parameter(torch.log(A))
# (args.d_inner, args.d_state)
(d_in, n) = self.A_log.shape # 获取A_log的维度
# 计算 ∆ A B C D, 这些属于状态空间参数.
# A, D 是 与输入无关的 (见Mamba论文Section 3.5.2 "Interpretation of A" for why A isn't selective)
# ∆, B, C 与输入有关(这是与线性是不变模型S4最大的不同,
# 也是为什么Mamba被称为 “选择性” 状态空间的原因)
# 计算矩阵A
A = -torch.exp(self.A_log.float()) # shape (d_in, n)
# 取D的值
D = self.D.float()
# 应用x的投影变换
# ( b,l,d_in) -> (b, l, dt_rank + 2*n)
x_dbl = self.x_proj(x) # (b, l, dt_rank + 2*n)
# 分割delta, B, C
# delta: (b, l, dt_rank). B, C: (b, l, n)
(delta, B, C) = x_dbl.split(split_size=[self.args.dt_rank, n, n], dim=-1)
# 应用dt_proj并计算delta
delta = F.softplus(self.dt_proj(delta)) # (b, l, d_in)
# 应用选择性扫描算法
y = self.selective_scan(x, delta, A, B, C, D)
return y
def selective_scan(self, u, delta, A, B, C, D):
"""执行选择性扫描算法,参考Mamba论文[1] Section 2和注释[2]. See:
- Section 2 State Space Models in the Mamba paper [1]
- Algorithm 2 in Section 3.2 in the Mamba paper [1]
- run_SSM(A, B, C, u) in The Annotated S4 [2]
经典的离散状态空间公式:
x(t + 1) = Ax(t) + Bu(t)
y(t) = Cx(t) + Du(t)
除了B和C (以及step size delta用于离散化) 与输入x(t)相关.
参数:
u: shape (b, l, d_in)
delta: shape (b, l, d_in)
A: shape (d_in, n)
B: shape (b, l, n)
C: shape (b, l, n)
D: shape (d_in,)
过程概述:
Returns:
output: shape (b, l, d_in)
Official Implementation:
selective_scan_ref(), https://github.com/state-spaces/mamba/blob/main/mamba_ssm/ops/selective_scan_interface.py#L86
Note: I refactored some parts out of `selective_scan_ref` out, so the functionality doesn't match exactly.
"""
# 获取输入u的维度
(b, l, d_in) = u.shape
# 获取矩阵A的列数
n = A.shape[1] # A: shape (d_in, n)
# 离散化连续参数(A, B)
# - A 使用 zero-order hold (ZOH) 离散化 (see Section 2 Equation 4 in the Mamba paper [1])
# - B is 使用一个简化的Euler discretization而不是ZOH.根据作者的讨论:
# "A is the more important term and the performance doesn't change much with the simplification on B"
# 计算离散化的A
# 将delta和A进行点乘,将A沿着delta的最后一个维度进行广播,然后执行逐元素乘法
# A:(d_in, n),delta:(b, l, d_in)
# A广播拓展->(b,l,d_in, n),deltaA对应原论文中的A_bar
deltaA = torch.exp(einsum(delta, A, 'b l d_in, d_in n -> b l d_in n'))
# delta、B和u,这个计算和原始论文不同
deltaB_u = einsum(delta, B, u, 'b l d_in, b l n, b l d_in -> b l d_in n')
# Perform selective scan (see scan_SSM() in The Annotated S4 [2])
# Note that the below is sequential, while the official implementation does a much faster parallel scan that
# is additionally hardware-aware (like FlashAttention).
# 执行选择性扫描,初始化状态x为零
x = torch.zeros((b, d_in, n), device=deltaA.device)
# 初始化输出列表ys
ys = []
for i in range(l):
# 更新状态x
# deltaA:((b,l,d_in, n)
# deltaB_u:( b,l,d_in,n)
# x:
x = deltaA[:, i] * x + deltaB_u[:, i]
# 计算输出y
y = einsum(x, C[:, i, :], 'b d_in n, b n -> b d_in')
# 将输出y添加到列表ys中
ys.append(y)
# 将列表ys堆叠成张量y
y = torch.stack(ys, dim=1) # shape (b, l, d_in)
# 将输入u乘以D并加到输出y上
y = y + u * D
return y
class RMSNorm(nn.Module):
"""
初始化RMSNorm模块,该模块实现了基于均方根的归一化操作。
参数:
d_model (int): 模型的特征维度。
eps (float, 可选): 为了避免除以零,添加到分母中的一个小的常数。
"""
def __init__(self,
d_model: int,
eps: float = 1e-5):
super().__init__()
self.eps = eps# 保存输入的eps值,用于数值稳定性。
# 创建一个可训练的权重参数,初始值为全1,维度与输入特征维度d_model相同。
self.weight = nn.Parameter(torch.ones(d_model))
def forward(self, x):
"""
计算输入x的均方根值,用于后续的归一化操作。
x.pow(2) 计算x中每个元素的平方。
mean(-1, keepdim=True) 对x的最后一个维度(特征维度)进行平方和求平均,保持维度以便进行广播操作。
torch.rsqrt 对求得的平均值取倒数和平方根,得到每个特征的均方根值的逆。
+ self.eps 添加一个小的常数eps以保持数值稳定性,防止除以零的情况发生。
x * ... * self.weight 将输入x与计算得到的归一化因子和可训练的权重相乘,得到最终的归一化输出。
"""
output = x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps) * self.weight
return output