前言
图论基础
图的相关概念
图的定义
图的分类
按数量分类:
按边的类型分类:
边权
简单图
度
路径
连通
无向图
有向图
图的存储
方法概述
代码
复杂度
前言
图论(Graph theory),是 OI 中的一样很大的一个模块,围绕它有很多高难度的算法以及高级的概念。这篇文章将介绍关于图论的一部分基础概念(干货满满!),话不多说,步入正题——
图论基础
(干货太多了,建议先收藏!)
图的相关概念
图的定义
图(graph)是一个二元组 G = (V(G), E(G))。其中 V(G) 是非空集,称为 点集(vertex set),对于 V 中的每个元素,我们称其为 顶点(vertex)或 节点(node),简称 点;E(G) 为 V(G) 各结点之间边的集合,称为 边集(edge set)。
我们一般用 G = (V, E) 表示图。
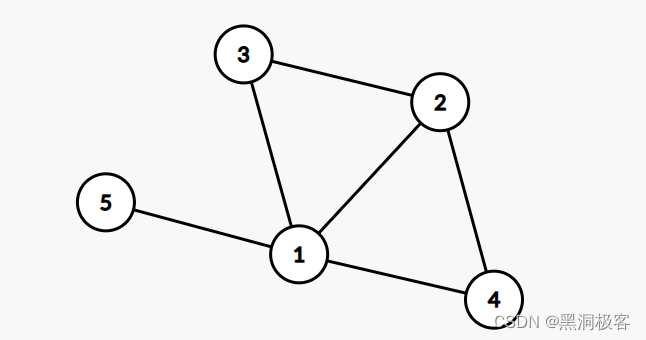
举个例子:
这就是一张图,1,2,3,4,5 就是它的节点。
推荐一个网站:Cs Academy
这里有十分好用的图编辑器,可以帮你加强理解图论!
图的分类
按数量分类:
当 V, E 都是有限集合时,称 G 为 有限图。
当 V 或 E 是无限集合时,称 G 为 无限图。
按边的类型分类:
图有多种,包括 无向图 (undirected graph),有向图 (directed graph),混合图 (mixed graph) 等。
若为无向图,则图中的每个元素为一个无序二元组 (u, v),称作 无向边 (undirected edge),简称 边 (edge),其中 u, v ∈ V。设 e = (u, v),则 u 和 v 称为 e 的 端点 (endpoint)。
若为有向图,则图中的每一个元素为一个有序二元组 (u, v),有时也写作 u → v,称作 有向边 (directed edge) 或 弧 (arc),在不引起混淆的情况下也可以称作 边 (edge)。设 e = u → v ,则此时 u 称为 e 的 起点 (tail),v 称为 e 的 终点 (head),起点和终点也称为 e 的 端点 (endpoint)。并称 u 是 v 的直接前驱,v 是 u 的直接后继。
若为混合图,则图中既有 有向边,又有 无向边。
还拿这张图来说,这是一个无向图。
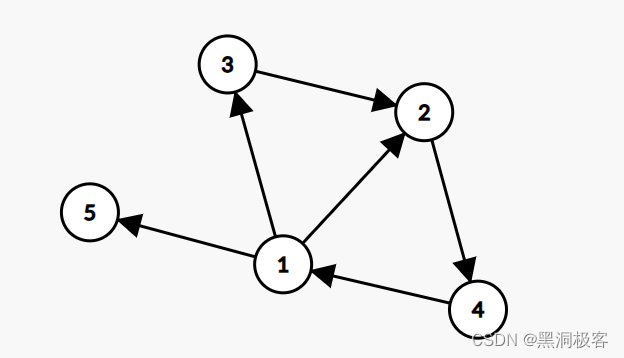
这就是一张有向图。
边权
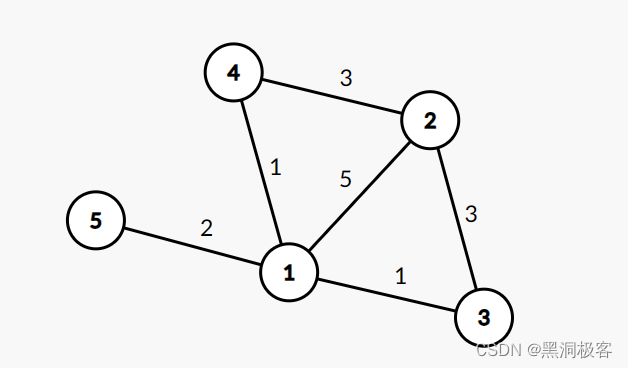
若图的每条边都被赋予一个数作为该边的 权,则称这张图为 赋权图。如果这些权都是正实数,就称为 正权图。
这张图就是一张 赋权图。
简单图
自环 (loop):对 E 中的边 e = (u,v) ,若 u = v ,则 e 被称作一个自环。
重边 (multiple edge):若 E 中存在两个完全相同的元素(边)e1,e2 ,则它们被称作(一组)重边。
简单图 (simple graph):若一个图中没有自环和重边,它被称为简单图。具有至少两个顶点的简单无向图中一定存在度相同的结点。
如果一张图中有自环或重边,则称它为 多重图 (multigraph)。
度
与一个顶点 v 关联的边的条数称作该顶点的 度 (degree),记作 d(v)。特别地,对于边 (v, v),则每条这样的边要对 d(v) 产生 2 的贡献。
对于无向简单图,有 d(v) = |N(v)|。
推论:在任意图中,度数为奇数的点必然有偶数个。(一笔画问题应该了解过吧)
若 d(v) = 0,则称 v 为 孤立点 (isolated vertex)。
若 d(v) = 1,则称 v 为 叶节点 (leaf vertex)/悬挂点 (pendant vertex)。
若 2 | d(v),则称 v 为 偶点 (even vertex),否则为 奇点 (odd vertex)。
若 d(v) = |V| - 1,则称 v 为 支配点 (universal vertex)。
(这些概念了解就行了,不需要特别去记)
对一张图,所有节点的度数的最小值称为 最小度 (minimum degree),最大值称为 最大度 (maximum degree)。
在有向图中,以一个顶点为起点的边的条数称为该顶点的 出度 (out-degree),以一个顶点 ![]() 为终点的边的条数称为该节点的 入度 (in-degree)。
为终点的边的条数称为该节点的 入度 (in-degree)。
如果给定一个序列 a,可以找到一个图 G,以其为度数列,则称 a 是 可图化 的。
如果给定一个序列 a,可以找到一个简单图 G,以其为度数列,则称 a 是 可简单图化 的。
路径
途径 (walk):途径是连接一连串顶点的边的序列,可以为有限或无限长度。形式化地说,一条有限途径 w 是一个边的序列 e1,e2,...,ek,使得存在一个顶点序列 v0,v1,...,vk 满足 ei = (v i-1,v i),其中 i ∈ [1, k] 。这样的途径可以简写为 v0 → v1 → v2 → ... → vk 。通常来说,边的数量 k 被称作这条途径的 长度(如果边是带权的,长度通常指途径上的边权之和,题目中也可能另有定义)。
看不懂?
(我也看不懂)为了更好地理解,可以把一张图当作一个地图,节点就是车站,边就是路,那么路径就是从一个车站到另一个车站的路线。如果这张图是赋权图,也就是说车站之间有了距离,那么路径的 长度 就是车站到车站的路线的长度。
回路 (circuit):对于一条路径 w![]() ,若 v0 = vk,则称 w 是一条回路。
,若 v0 = vk,则称 w 是一条回路。
连通
无向图
对于一张无向图 G = (V,E),对于 u,v ∈ V,若存在一条途径使得 v0 = u, vk = v,则称 u 和 v 是 连通的 (connected)。由定义,任意一个顶点和自身连通,任意一条边的两个端点连通。
若无向图 G = (V,E),满足其中任意两个顶点均连通,则称 G 是 连通图 (connected graph),这一性质称作 连通性 (connectivity)。
有向图
对于一张有向图 G = (V,E),对于 u,v ∈ V,若存在一条途径使得 v0 = u, vk = v, 则称 u 可达 v。由定义,任意一个顶点可达自身,任意一条边的起点可达终点。(无向图中的连通也可以视作双向可达。)
若一张有向图的节点两两互相可达,则称这张图是 强连通的 (strongly connected)。
若一张有向图的边替换为无向边后可以得到一张连通图,则称原来这张有向图是 弱连通的 (weakly connected)。
到这,你已经看过了图的大部分概念。全是干货,如果还没理解,可以收藏起来慢慢看!
图的存储
本文会介绍最常用的存储方法,也就是:直接存边。
方法概述
使用一个数组来存边,数组中的每个元素都包含一条边的起点与终点(带边权的图还包含边权)。
代码
struct Edge {
int u, v;
};
vector<Edge> e;复杂度
查询是否存在某条边:O(m) 。
遍历一个点的所有出边:O(m) 。
遍历整张图:O(nm) 。
空间复杂度:O(m) 。
干货太多,整理得肝疼,求个点赞收藏不过分吧!(求求了!)
本文就到这里,下次再见!