文章目录
- 1. 矩阵空间
- 2. 微分方程
- 3. 秩为1的矩阵
- 4. 图
1. 矩阵空间
我们以3X3的矩阵空间 M 为例来说明相关情况。目前矩阵空间M中只关心两类计算,矩阵加法和矩阵数乘。
- 对称矩阵-子空间-有6个3X3的对称矩阵,所以为6维矩阵空间
- 上三角矩阵-子空间-有6个3X3的上三角矩阵,所以为6维矩阵空间
矩阵M的基础基有9个,表示如下
[ 1 0 0 0 0 0 0 0 0 ] ; [ 0 1 0 0 0 0 0 0 0 ] ; [ 0 0 1 0 0 0 0 0 0 ] ; [ 0 0 0 1 0 0 0 0 0 ] ; (1) \begin{bmatrix}1&0&0\\\\0&0&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&1&0\\\\0&0&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&1\\\\0&0&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\1&0&0\\\\0&0&0\\\\\end{bmatrix};\tag{1} 100000000 ; 000100000 ; 000000100 ; 010000000 ;(1)
[ 0 0 0 0 1 0 0 0 0 ] ; [ 0 0 0 0 0 1 0 0 0 ] ; [ 0 0 0 0 0 0 1 0 0 ] ; [ 0 0 0 0 0 0 0 1 0 ] ; [ 0 0 0 0 0 0 0 0 1 ] ; (2) \begin{bmatrix}0&0&0\\\\0&1&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&1\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&0\\\\1&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&0\\\\0&1&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&0\\\\0&0&1\\\\\end{bmatrix};\tag{2} 000010000 ; 000000010 ; 001000000 ; 000001000 ; 000000001 ;(2)
2. 微分方程
- 假设我们有如下微分方程:
d 2 y d x 2 + y = 0 (3) \frac{\mathrm{d}^2y}{\mathrm{d}x^2}+y=0\tag{3} dx2d2y+y=0(3) - 零空间解表示如下:
y 1 = sin ( x ) ; y 2 = cos ( x ) (4) y_1=\sin(x);y_2=\cos(x)\tag{4} y1=sin(x);y2=cos(x)(4) - 通解表示如下:
y = c 1 sin ( x ) + c 2 cos ( x ) (5) y=c_1\sin(x)+c_2\cos(x)\tag{5} y=c1sin(x)+c2cos(x)(5)
以上可以用 sin ( x ) \sin(x) sin(x)和 cos ( x ) \cos(x) cos(x)当做解来表示解空间,所以微分方程的解空间为2.
3. 秩为1的矩阵
假设我们有一个秩为1的矩阵A ,表示如下:
A
=
[
1
4
5
2
8
10
]
=
[
1
2
]
2
×
1
[
1
4
5
]
1
×
3
(6)
A=\begin{bmatrix}1&4&5\\\\2&8&10\end{bmatrix}=\begin{bmatrix}1\\\\2\end{bmatrix}_{2\times1}\begin{bmatrix}1&4&5\end{bmatrix}_{1\times3}\tag{6}
A=
1248510
=
12
2×1[145]1×3(6)
- 所有的秩为1的矩阵均可以分解为列向量乘以行向量。
- 小结:
我们可以通过组合秩为1的矩阵来构造我们想要的秩的矩阵。
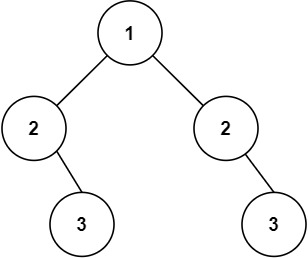
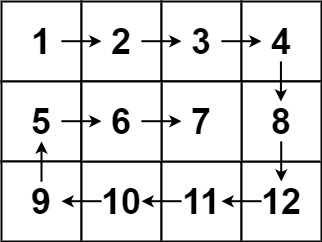
4. 图
我们知道一个图可以有节点和边组成
G
r
a
p
h
=
[
n
o
d
e
s
,
e
d
g
e
s
]
(7)
Graph=[nodes,edges]\tag{7}
Graph=[nodes,edges](7)

![【洛谷 P8655】[蓝桥杯 2017 国 B] 发现环 题解(邻接表+并查集+路径压缩)](https://img-blog.csdnimg.cn/direct/378c2e3302ba420bac3cc8056a199fc9.jpeg)