一、理论基础
文章讲解:https://programmercarl.com/%E8%B4%AA%E5%BF%83%E7%AE%97%E6%B3%95%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
1.贪心的定义
贪心的本质是选择每一阶段的局部最优解,从而达到全局最优解。例如,有一堆钞票,你可以拿走十张,如果想要拿走的金钱价值最大,那么每次都拿剩余钞票中价值最大的一张即可。而另一类问题,满足每个阶段都是局部最优解,但最后不一定是全局最优解。比如有一堆盒子,你有一个背包体积为n,如何把背包尽可能装满,如果还每次选最大的盒子,就不行了,因为可能选体积小的盒子反而能最大程度利用空间(相信大家开学装行李箱的时候都深有体会)。
2.贪心的套路
贪心并没有固定套路,偏意识流。难点在于如何看出局部最优能够推出全局最优。现在也没有固定的方法能够说明某题就是贪心,纯靠自己手动模拟,如果模拟可行,就可以试一试贪心策略,如果不可行,可能需要动态规划。拿不准的时候可以举反例,如果想不到反例,那么就试一试贪心吧。当然也可以进行严格的数学推理来表明此题就适合贪心,但不是数学专业的人建议不要这么做,因为比较复杂,面试或者比赛的时候并不要求参与者能够当场证明贪心的合理性。因此,贪心说白了就是常识推导+举反例。
3.贪心一般解题步骤
贪心算法一般分为如下四步:
(1)将问题分解为若干个子问题
(2)找出适合的贪心策略
(3)求解每一个子问题的最优解
(4)将局部最优解堆叠成全局最优解
但这个四步其实过于理论化了,我们平时在做贪心类的题目 很难去按照这四步去思考。做题的时候,只要想清楚 局部最优 是什么,如果推导出全局最优,就够了。
二、LeetCode 455.分发饼干
题目链接/文章讲解/视频讲解:https://programmercarl.com/0455.%E5%88%86%E5%8F%91%E9%A5%BC%E5%B9%B2.html
状态:已解决
1.思路
因为是饼干是离散数据,这意味着饼干不可切分,即使一块饼干尺寸大于孩子的胃口,也只能给孩子喂一整块饼干;那么,对于这样的问题,就用最大饼干尽量去喂最大胃口的孩子(或者小饼干喂小胃口的孩子),即贪心策略,相当于最大化利用每块饼干,如果拿大饼干喂小胃口孩子造成的浪费就会很大,因为可能还存在其他较小饼干也能喂饱小孩子,而你用大饼干去喂,其他饼干又较小,那么大胃口的孩子就无法得到满足。
如图,是大饼干满足大胃口的情况:
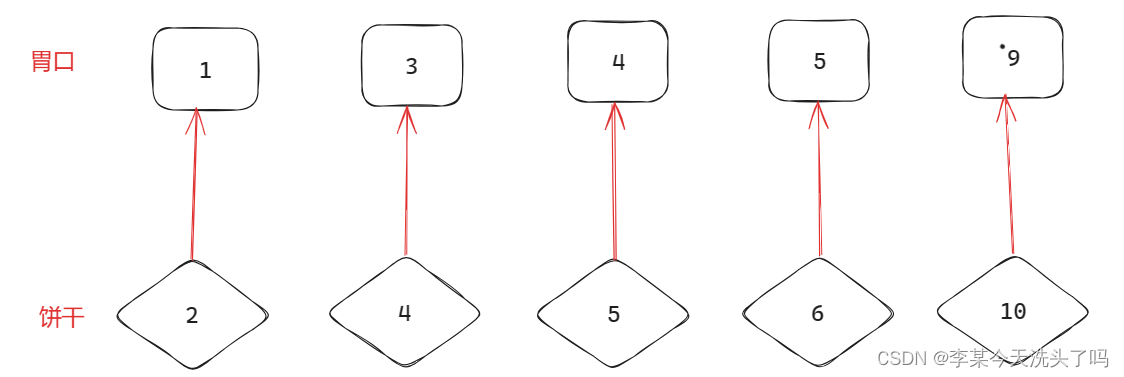
如果有一个饼干不满足大饼干喂大胃口,就会出现以下情况,造成部分饼干浪费且减少了满足孩子数。

明白原理后,思路就很清晰了。我们需要先对饼干和胃口的数组进行排序,排序后,分别从最大值开始,控制饼干和胃口进行对比,如果该饼干大于等于该胃口,饼干和胃口都向前移动一位,如果小于,则只移动胃口,找能被该饼干喂饱的最大胃口。
注意,遍历顺序是胃口在外,饼干在内。胃口为外循环代表每次无论喂饱成功都会向前移动一位,相当于,饼干是不变量,需要滑动胃口找能被该饼干喂饱的最大胃口,饼干只有在找到能满足的胃口后才往前移。
2.代码实现
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int index = s.size()-1;
int result=0;
for(int i=g.size()-1;i>=0;i--){
if(index>=0 && s[index]>=g[i]){
result++;
index--;
}
}
return result;
}
};三、376.摆动序列
题目链接/文章讲解/视频讲解:https://programmercarl.com/0376.%E6%91%86%E5%8A%A8%E5%BA%8F%E5%88%97.html
状态:已解决
1.思路
这道题需要画图理解,例如,以示例二来举例:
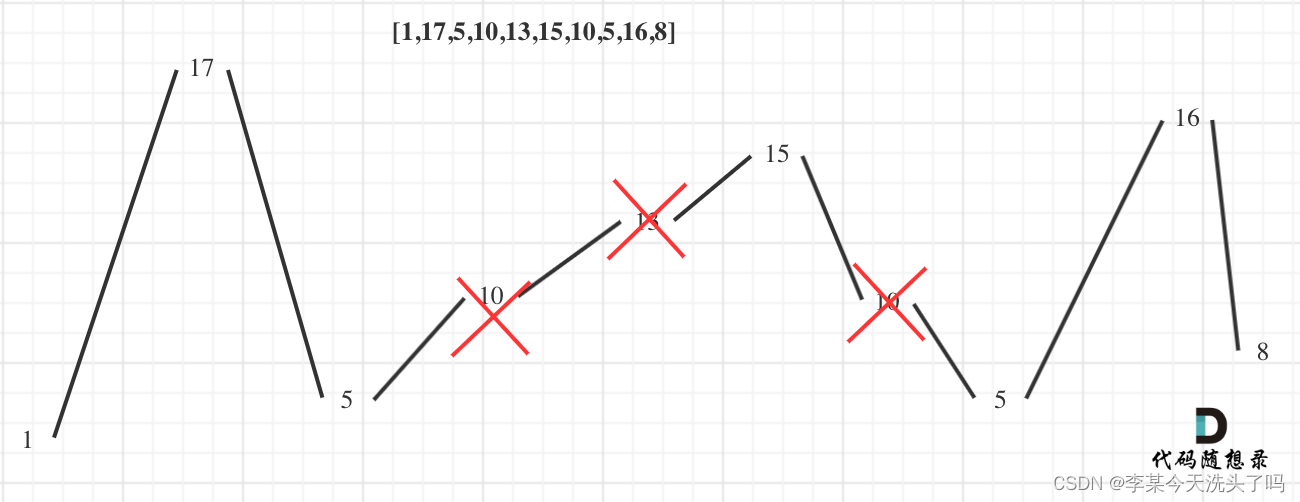
画图图形后,很容易就看出最大摆动序列的长度是峰值的个数(包括最大和最小)。其中,
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
局部最优推出全局最优,并且举不出反例,因此可以试试贪心做法。因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了(相当于是删除单一坡度上的节点,然后统计长度)
在计算是否有峰值的时候,大家知道遍历的下标 i ,计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i]),如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。
这是我们思考本题的一个大题思路,但本题要考虑三种情况:
- 情况一:上下坡中有平坡
- 情况二:数组首尾两端
- 情况三:单调坡中有平坡
(1)情况一:上下坡中有平坡
例如,对于数组[1,2,2,2,1],如图
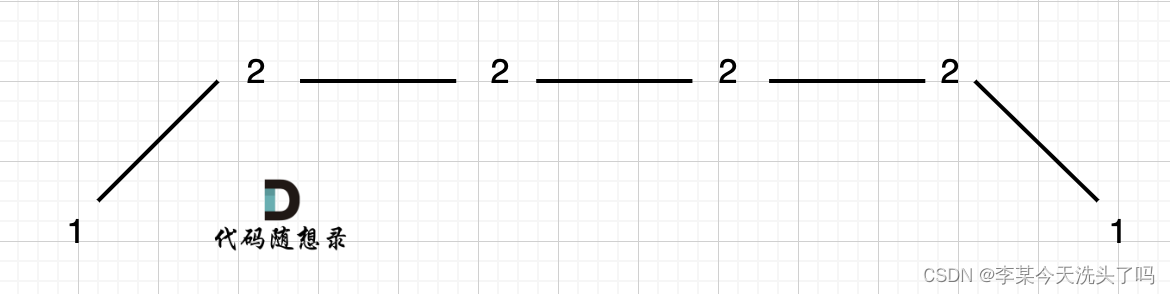
那么这种上下坡包含平坡的数组摇摆序列长度为多少呢?其实为3,整个平坡可以看作一个峰值。删除左边两个或者右边两个2,构造峰值。为了tong'yi
2.代码实现
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
int curdiff = 0;
int prediff = 0;
int result = 1;
for(int i=0;i<nums.size()-1;i++){
curdiff = nums[i+1]-nums[i];
if((prediff >=0 && curdiff < 0) || (prediff <=0 && curdiff >0)){
prediff = curdiff;
result++;
}
}
return result;
}
};四、53. 最大子序和
题目链接/文章讲解/视频讲解:https://programmercarl.com/0053.%E6%9C%80%E5%A4%A7%E5%AD%90%E5%BA%8F%E5%92%8C.html
状态:已解决
1.思路
这题我会做!这种求连续子序列最大值类型题的本质是:如果前面的序列和对自身有利才连接序列,否则从自身作为起点重新开始选取序列,也就是自己永远不吃亏。题目要求求具有最大和的连续子数组,我们知道,连续子数组的和=前面连续子数组的和+nums[i],那么怎么选取子序列能够使和最大呢?假如当前在nums[i]的位置,如果前面选取的连续子序列的和<0,那么就说明,nums[i]加上前面的连续子序列后只会拉低nums[i]的值,也就是得到相加结果sum<num[i],这时候单独选nums[i]的结果都比已有连续序列的和大,故我们此时不再连上前面的子序列,而是自立山头,从nums[i]开始做新的序列起点;只有在前面连续子序列的和大于0时,代表连上前面的连续子序列对nums[i]有利,得到相加结果sum>num[i],因此,选择连上前面的序列,扩大连续子序列的范围。
注意,是连续和小于0时才不选择连接,而不是遇到负数就不连。有人可能觉得遇到负数不是会减小sum吗,但是只有sum仍然大于0,我们就可以把前面的增益效果传递到后面的正数部分,使得正数部分加上后大于自身。例如,假如nums[i]<0,但是连续子数组的和=前面连续子数组的和+nums[i]>0,这种情况仍然是可以被保存的,因为加上下一个num[i+1]后,新的sum值仍会大于nums[i+1]的值。举个示例,[4,-1,5],i此时等于1,显然,nums[-1]=-1<0,但是加上前面的序列和为3,3加到5身上为8,大于5本身,故只有连续和小于0时才不被连接。
2.代码实现
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int result=-100000;
int nowSum = 0;
for(int i=0;i<nums.size();i++){
if(nowSum >= 0){
nowSum += nums[i];//如果前面的和为非负数,那么证明前面的和对我有利,故加之
}
else{
nowSum = nums[i];//如果前面的和为负数,那么前面的和对我不利,不加,
//我自己就比它们的和大了,故作为新起点开始
}
result = (result>nowSum)?result:nowSum;
}
return result;
}
};