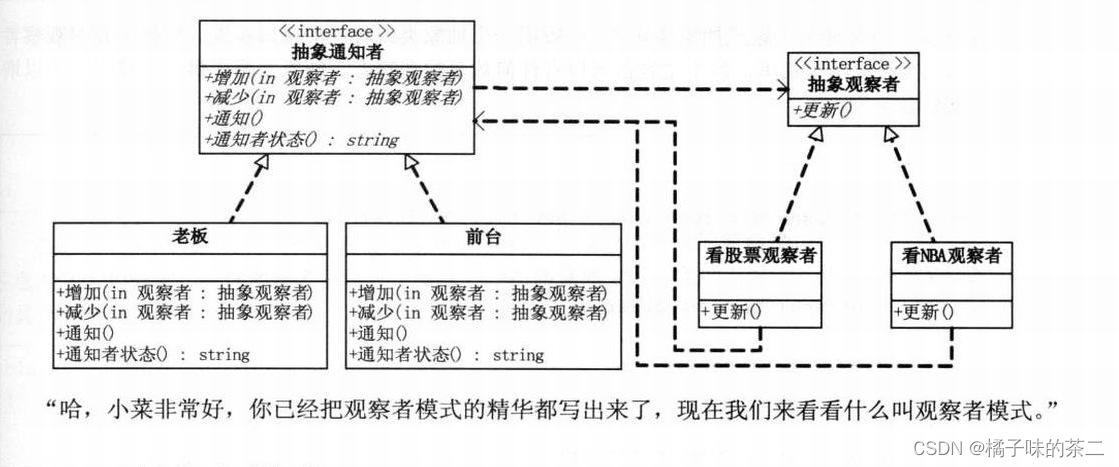
E. Pokémon Arena：

题目大意：

思路解析：

可以想到的是，可以用最短路来解决这个问题，但是如果简单的建图的话，时间复杂度将会达到 O(n*n*m)，我们考虑怎么减少图中边的个数。

我们考虑一个颜色，从这个点能去的点，能不能去这个点可以用一个代价数组判断，然后我们再考虑到达的点，是否之前通过其他颜色到达过，如果没有，我们衍生这个点其他的颜色。点移动时，我们让他移动到在这个颜色上离他最近的点，如果让他混乱移动，可能第一次到达这个点时代价不是最低的情况，那么这样的衍生并不是好的操作。

那么每个点我们最多只需要访问一次，一个点最多有m个颜色，那么最多可能包含 n*m种情况。那么便可以在此基础上利用最短路即可。

代码实现：

import java.io.*;
import java.math.BigInteger;
import java.util.*;

import static java.util.Collections.*;

public class Main {
    static long inf = (long) 2e18;

    public static void main(String[] args) throws IOException {
        int t = f.nextInt();
        while (t > 0) {
            solve();
            t--;
        }

        w.flush();
        w.close();
        br.close();
    }


    public static void solve() {
        int n = f.nextInt();
        int m = f.nextInt();
        int[] c = new int[n+1];
        int[][] a = new int[n+1][m+1];
        int[][] rk = new int[n+1][m+1];
        int[][] dec = new int[n+1][m+1];
        long[][] dist = new long[n+1][m+1];
        for (int i = 0; i < n + 1; i++) {
            Arrays.fill(dist[i], inf);
        }
        for (int i = 0; i < m + 1; i++) {
            dist[1][i] = 0;
        }
        for (int i = 0; i < n; i++) {
            c[i+1] = f.nextInt();
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                a[i+1][j+1] = f.nextInt();
            }
        }
        for (int i = 1; i <= m; i++) {
            ArrayList<int[]> bq = new ArrayList<>();
            for (int j = 1; j <= n; j++) {
                bq.add(new int[] {a[j][i], j});
            }
            bq.sort(new Comparator<int[]>() {
                @Override
                public int compare(int[] o1, int[] o2) {
                    return o1[0] - o2[0];
                }
            });
            int cnt = 1;
            for (int[] cur : bq) {
                dec[cnt][i] = cur[1];
                rk[cur[1]][i] = cnt++;
            }
        }
        int[] vis = new int[n+1];
        vis[1] = 1;
        PriorityQueue<long[]> q = new PriorityQueue<>(new Comparator<long[]>() {
            @Override
            public int compare(long[] o1, long[] o2) {
                return Long.compare(o1[0], o2[0]);
            }
        });
        for (int i = 1; i <= m; i++) {
            q.add(new long[] {dist[1][i], 1, i});
        }
        long ans = inf;
        while (!q.isEmpty()){
            long[] cur = q.poll();
            int x = (int) cur[1]; int t = (int) cur[2]; long w = cur[0];
            if (w > dist[x][t]) continue;
            if (x == n) ans = Math.min(ans, w + c[n]);
            if (rk[x][t] < n){
                int y = dec[rk[x][t] + 1][t];
                if (w < dist[y][t]){
                    dist[y][t] = w;
                    q.add(new long[] {dist[y][t], y, t});
                }
            }

            if (rk[x][t] > 1){
                int y = dec[rk[x][t] - 1][t];
                if (w + a[x][t] - a[y][t]< dist[y][t]){
                    dist[y][t] = w + a[x][t] - a[y][t];
                    q.add(new long[] {dist[y][t], y, t});
                }
            }

            if (vis[x] == 0){
                vis[x] = 1;
                for (int i = 1; i <= m; i++) {
                    if (w + c[x] < dist[x][i]){
                        dist[x][i] = w + c[x];
                        q.add(new long[] {dist[x][i], x, i});
                    }
                }
            }
        }
        w.println(ans);
    }


    static PrintWriter w = new PrintWriter(new OutputStreamWriter(System.out));
    static Input f = new Input(System.in);
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

    static class Input {
        public BufferedReader reader;
        public StringTokenizer tokenizer;

        public Input(InputStream stream) {
            reader = new BufferedReader(new InputStreamReader(stream), 32768);
            tokenizer = null;
        }

        public String next() {
            while (tokenizer == null || !tokenizer.hasMoreTokens()) {
                try {
                    tokenizer = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    throw new RuntimeException(e);
                }
            }
            return tokenizer.nextToken();
        }

        public String nextLine() {
            String str = null;
            try {
                str = reader.readLine();
            } catch (IOException e) {
                // TODO 自动生成的 catch 块
                e.printStackTrace();
            }
            return str;
        }

        public int nextInt() {
            return Integer.parseInt(next());
        }

        public long nextLong() {
            return Long.parseLong(next());
        }

        public Double nextDouble() {
            return Double.parseDouble(next());
        }

        public BigInteger nextBigInteger() {
            return new BigInteger(next());
        }
    }
}