【LetMeFly】2192.有向无环图中一个节点的所有祖先：拓扑排序

力扣题目链接：https://leetcode.cn/problems/all-ancestors-of-a-node-in-a-directed-acyclic-graph/

给你一个正整数 n ，它表示一个 有向无环图 中节点的数目，节点编号为 0 到 n - 1 （包括两者）。

给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。

请你返回一个数组 answer，其中 answer[i]是第 i 个节点的所有 祖先 ，这些祖先节点 升序 排序。

如果 u 通过一系列边，能够到达 v ，那么我们称节点 u 是节点 v 的 祖先 节点。

 

示例 1：

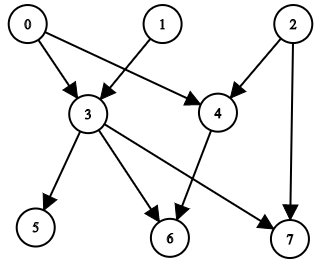
输入：n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出：[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释：
上图为输入所对应的图。
- 节点 0 ，1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ，1 和 3 。
- 节点 6 有 5 个祖先 0 ，1 ，2 ，3 和 4 。
- 节点 7 有 4 个祖先 0 ，1 ，2 和 3 。

示例 2：

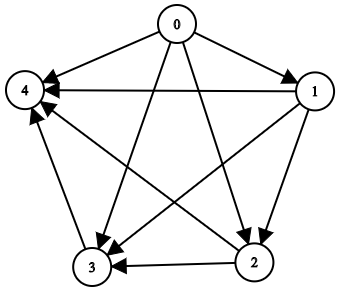
输入：n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
输出：[[],[0],[0,1],[0,1,2],[0,1,2,3]]
解释：
上图为输入所对应的图。
- 节点 0 没有任何祖先。
- 节点 1 有 1 个祖先 0 。
- 节点 2 有 2 个祖先 0 和 1 。
- 节点 3 有 3 个祖先 0 ，1 和 2 。
- 节点 4 有 4 个祖先 0 ，1 ，2 和 3 。

 

提示：

• 1 <= n <= 1000
• 0 <= edges.length <= min(2000, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi <= n - 1
• fromi != toi
• 图中不会有重边。
• 图是 有向 且 无环 的。

解题方法：拓扑排序

遍历所有边，记录下：每个节点的入度（有多少条边指向这个节点）、每个节点都指向哪些节点。

使用一个队列，将所有入度为0的点入队。当队列非空时，不断从队首取出节点。遍历这个节点的所有子节点，子节点入度减一（若减为0则入队），子节点的祖先节点加上这个节点以及这个节点的祖先节点。

最终返回每个节点的祖先节点。（可以使用哈希表来存放一个节点的祖先节点，这样便于在$O(1)$的时间复杂度内完成新祖先节点的插入与去重，最终再转为数组并排序）

• 时间复杂度$O(n\times len(edges)+n^2\log n)$：拓扑排序$n\times len(edges)$，后序对每个节点的祖先节点排序(最多)都是$n\log n$
• 空间复杂度$O(n^2)$：等于答案的空间复杂度（我们使用哈希表辅助中间过程的运算消耗空间相同）

AC代码

C++

class Solution {
public:
    vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
        vector<unordered_set<int>> father(n);
        vector<int> degree(n);
        vector<vector<int>> graph(n);
        for (vector<int>& edge : edges) {
            graph[edge[0]].push_back(edge[1]);
            degree[edge[1]]++;
        }
        queue<int> q;
        for (int i = 0; i < n; i++) {
            if (!degree[i]) {
                q.push(i);
            }
        }
        while (q.size()) {
            int thisNode = q.front();
            q.pop();
            for (int nextNode : graph[thisNode]) {
                father[nextNode].insert(thisNode);
                for (int thisFather : father[thisNode]) {
                    father[nextNode].insert(thisFather);
                }
                degree[nextNode]--;
                if (!degree[nextNode]) {
                    q.push(nextNode);
                }
            }
        }
        vector<vector<int>> ans(n);
        for (int i = 0; i < n; i++) {
            for (int t : father[i]) {
                ans[i].push_back(t);
            }
            sort(ans[i].begin(), ans[i].end());
        }
        return ans;
    }
};

Python

# from typing import List
# from collections import deque


class Solution:
    def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        father = [set() for _ in range(n)]
        degree = [0] * n
        graph = [[] for _ in range(n)]
        for x, y in edges:
            degree[y] += 1
            graph[x].append(y)
        q = deque()
        for i in range(n):
            if not degree[i]:
                q.append(i)
        while q:
            thisNode = q.popleft()
            for nextNode in graph[thisNode]:
                father[nextNode].add(thisNode)
                father[nextNode].update(father[thisNode])
                degree[nextNode] -= 1
                if not degree[nextNode]:
                    q.append(nextNode)
        return [sorted(list(i)) for i in father]

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/137376368