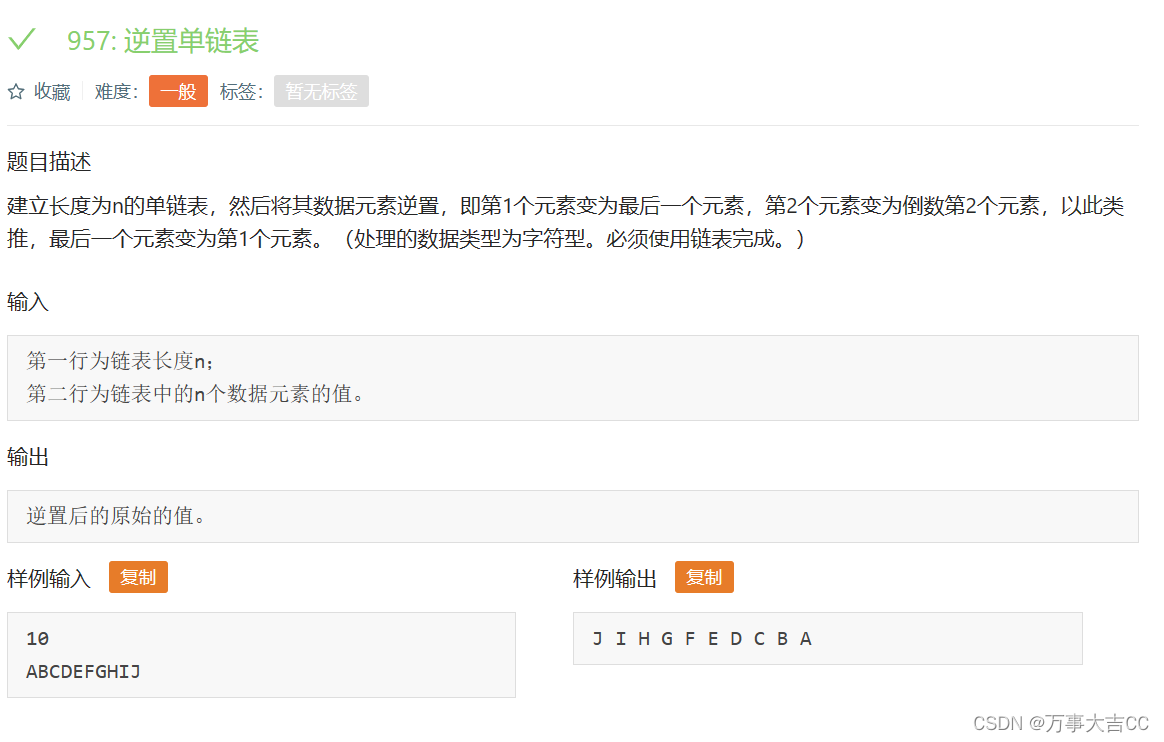
1388. 游戏 - AcWing题库

所需知识：博弈论，区间dp

由于双方都采取最优的策略来取数字，所以结果为确定的，有可能会有多个不同的过程，但是我们只需要关注最终结果就行了。

方法一：

定义dp[i][j] 表示区间i到j中先手能取得的最大值，依次遍历区间，最后判断最大值，因为区间长度长的来源必定是区间长度短的，所以我们可以第一层遍历区间的长度，第二层遍历区间的左端点。

状态转移方程式：dp[i][j]=max(w[i]+s[j]-s[i]-dp[i+1][j],w[j]+s[j-1]-s[i-1]-dp[i][j-1]);

对于状态转移方程式的解释：

若选择左边的数字，则，下一个人在i+1到j中选择对于他自己而言的最优解，所以，dp[i][j] 为w[i] +s[j]-s[i] (i+1到j的区间和) -dp[i+1][j](减去下一个人能拿的最大值)。

若选择右边的数字，则，下一个人在i到j-1中选择对于他自己而言的最优解，所以，dp[i][j] 为w[j] +s[j-1]-s[i-1] (i到j-1的区间和) -dp[i][j-1](减去下一个人能拿的最大值)。

最后取最大值，即为答案。

C++代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int N;
int dp[105][105];
int w[105],s[105];
int main()
{
    cin>>N;
    for (int i = 1; i <= N; i ++ ){
        cin>>w[i];
        s[i]=s[i-1]+w[i];
    }
    for(int len=1;len<=N;len++){
        for(int i=1;i<=N;i++){
            int j=i+len-1;
            dp[i][j]=max(w[i]+s[j]-s[i]-dp[i+1][j],w[j]+s[j-1]-s[i-1]-dp[i][j-1]);
        }
    }
    
    cout<<dp[1][N]<<' '<<s[N]-dp[1][N];
    return 0;
}

方法二：

定义dp[i][j] 表示在区间i到j内先手能拿到的最优值减去后手拿的最优值，即为A-B（A为方法一中的区间最大值，B为区间和减最大值）；

遍历方法仍和方法一一样，先遍历一遍区间长度，然后再遍历左端点的值。

状态转移方程式：dp[i][j]=max(w[i]-dp[i+1][j],w[j]-dp[i][j-1]);

对于状态转移方程式的解释：

若取左边的数,则下一个人在区间i+1到j中取dp[i+1][j]表示该区间中的max（B-A），所以-dp[i+1][j]表示该区间中A-B的最大值，在加上w[i],表示区间i到j中A-B的最大值；

同理，若取右边的数,则下一个人在区间i到j-1中取dp[i][j-1]表示该区间中的max（B-A），所以-dp[i][j-1]表示该区间中A-B的最大值，在加上w[j],表示区间i到j中A-B的最大值；

最后dp[1][N]表示该区间内A-B的最大值，又因为A+B=sum（sum为所有元素和）；

联立两个方程解得，A=（dp[1][N]+sum）/2;B=(sum-dp[1][N])/2;

C++代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int N;
int dp[105][105];
int w[105],s[105];
int sum=0;
int main()
{
    cin>>N;
    for (int i = 1; i <= N; i ++ ){
        cin>>w[i];
        sum+=w[i];
    }
    for(int len=1;len<=N;len++){
        for(int i=1;i+len-1<=N;i++){
            int j=i+len-1;
            dp[i][j]=max(w[i]-dp[i+1][j],w[j]-dp[i][j-1]);
        }
    }
    
    cout<<(sum+dp[1][N])/2<<' '<<(sum-dp[1][N])/2;
    return 0;
}