目录
保证给你讲透讲懂
第一种:埃氏筛法
第二种:欧拉筛法
题目:质数率
题目:不喜欢的数
思路:
问题:1~n 中筛选出所有素数(质数)
有两种经典的时间复杂度较低的筛法,即埃氏筛法和欧拉筛法。
既然是筛子,那么核心思想就是:根据当前的数筛掉后面的一些不合法数据,留下的每个数都是质数。
第一种:埃氏筛法
(也是最好理解的筛子,不过速度O(n*loglogn))
首先2是最小的素数,将表中所有的2的倍数划去。
表中剩下的最小的数字就是3,所以3是素数。再将表中所有的3的倍数划去……
以此类推,如果表中剩余的最小的数是几,几就是素数。然后将其倍数筛掉
核心代码:
第二个for为什么从i*i开始:
答:我们会先筛2的所有倍数,然后是3的倍数,但是后面在筛3的倍数的时候我们还需要从2开始筛吗?筛掉3*2?这个之前在筛2的时候就已经标记过了的,那么直接从3本身筛开始多好啊。
int eprime(int n){
judge[0]=judge[1]=1;
for(int i=2;i<=n;i++){
if(judge[i]==0){
prime[cnt++]=i;
for(int j=i*i;j<=n;j+=i) judge[j]=1;//直接从i本身开始筛
}
}
return cnt;
}重点: 虽然埃氏筛易理解,但是个别时候还是会被卡的。
我们深入理解埃氏筛的思想:
要想得到 n以内的质数,就要把不大于根号n的质数的倍数全部剔除,剩下的就是质数。从 2 开始,把 2 的倍数(不包括本身)标记为合数,然后向后枚举,查到一个未标记为合数的,就把它的倍数(不包括本身)标记为合数。以此类推,查到 n 为止。
例如一个数 24,它会被 2 标记一次,被3标记一次。如果这个数的质因数较多,那么重复的就会更多,每个已经被筛掉的数重复的被筛,这就会导致时间变长
(放心,欧拉来了)
第二种:欧拉筛法
欧拉筛法的原理同埃氏筛法,只不过多了一个判断删除与标记最小质因子的过程。
在埃氏筛法中,一个合数来说可能会被筛多次,比如6可以被2筛去,也可以被3筛去,而欧拉筛要做的事情就是让一个合数只被筛一次。
我们规定这个合数只会被它的最小质因数筛掉。这样能保证每个合数只会被筛一次。
核心代码
int oprime(int n){//线性筛O(n)速度求出小于n的所有质数!!!
judge[0]=judge[1]=1;
for(int i=2;i<=n;i++){
if(!judge[i]) prime[cnt++]=i;//没有被标记过的数必然是质数,加入质数中
for(int j=0;prime[j]*i<=n;j++){//质数性倍增(只枚举当然已放入的质数)
judge[prime[j]*i]=true;//此数的质数倍数加入标记中
if(i%prime[j]==0)break;//保证了一个合数只被它最小的质因子枚举标记,而一个质数只会一直枚举标记到本身
}
}
return cnt;
}过程如下:
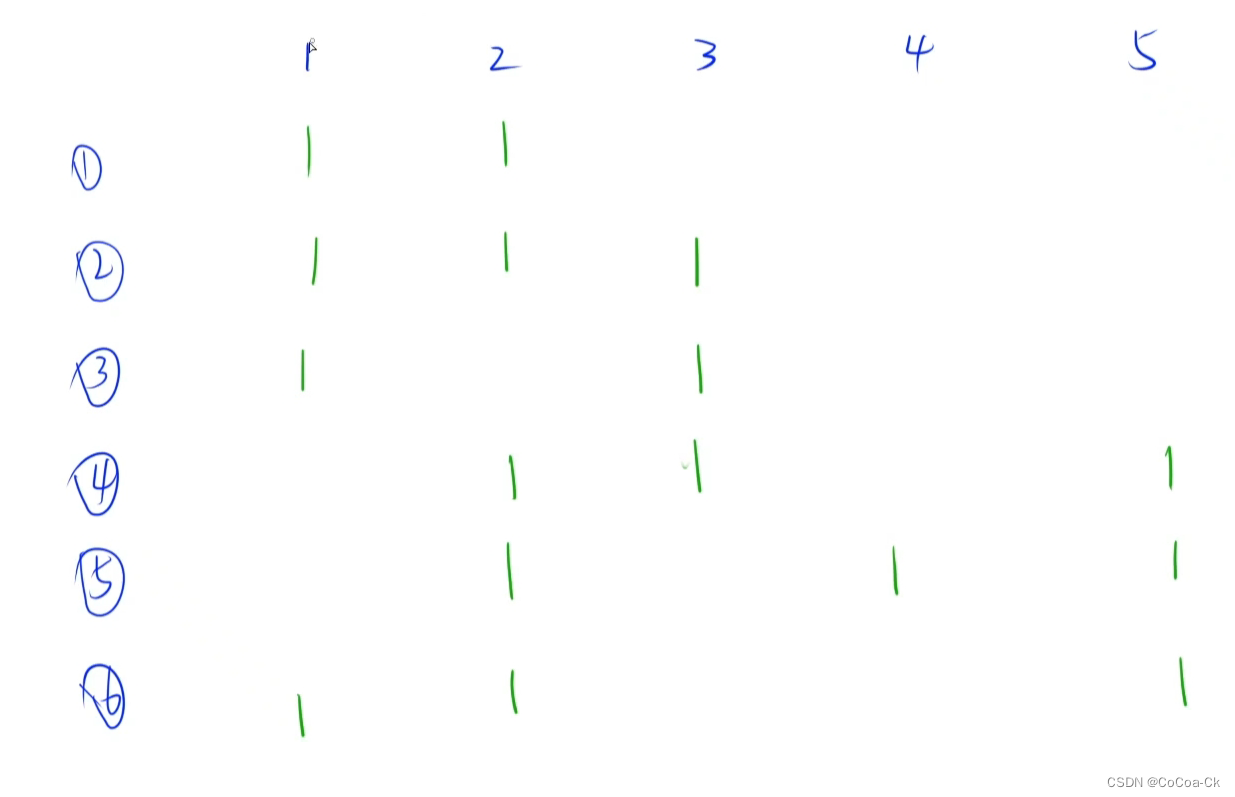
从 2开始:2 加入 prime 数组,从小到大枚举质数(现在只有 2),筛掉质数与 2 的乘积(4 被筛掉)。
到了 3: 3 加入 prime 数组,从小到大枚举质数(此时有 2,3),筛掉质数与 3 的乘积(6,9 被筛掉)。
到了 4: 4 没加入 prime 数组,枚举质数(有2,3),筛掉 8 后,因为 4mod2=0,触发退出条件。(不触发,就会筛掉 12,而 12=2×2×3,又会被 2 和 6筛一次,懂了吗)
以此类推,可做出一张表:
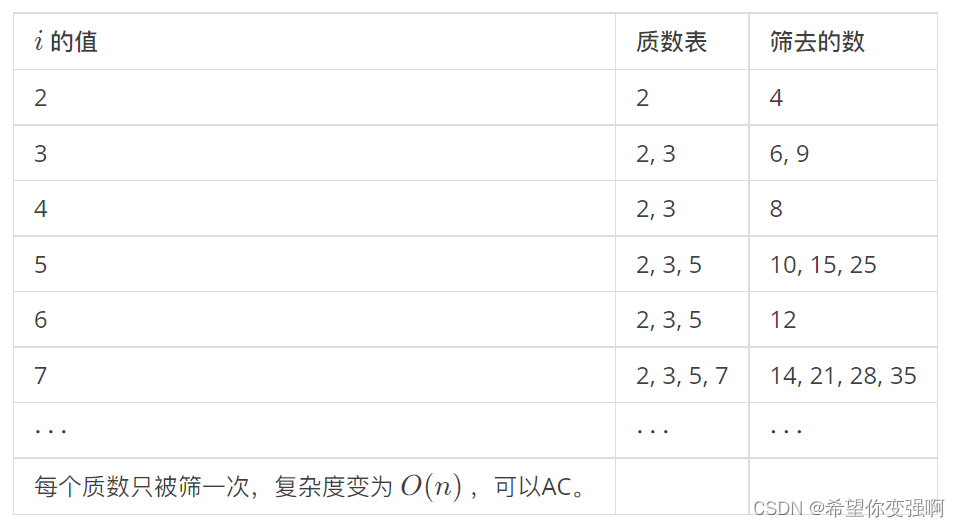
不难发现保证一个合数只被它最小的质因子枚举标记,而一个质数只会一直枚举标记到本身。保证了合数只被一次筛掉。
下面是完整代码:
#include <bits/stdc++.h>//线性筛模板
using namespace std;
bool judge[1000000];
int n,cnt,prime[1000];
int oprime(int n){//线性筛O(n)速度求出小于n的所有质数!!!
judge[0]=judge[1]=1;
for(int i=2;i<=n;i++){
if(!judge[i]) prime[cnt++]=i;//没有被标记过的数加入质数中
for(int j=0;prime[j]*i<=n;j++){//1,质数性倍增(只枚举当然已放入的质数)
judge[prime[j]*i]=true;//此数的质数倍数加入标记中(必然不是质数)
if(i%prime[j]==0)break;//2,保证一个合数只被它最小的质因子枚举标记,而一个质数只会一直枚举标记到本身
}
}
return cnt;
}
int eprime(int n){
judge[0]=judge[1]=1;
for(int i=2;i<=n;i++){
if(judge[i]==0){
prime[cnt++]=i;
for(int j=i*i;j<=n;j+=i) judge[j]=1;
}
}
return cnt;
}
int main(){
cin>>n;eprime(n);
//oprime(n);
for(int i=0;i<cnt;i++){
cout<<prime[i]<<' ';
}
return 0;
}以上算法只有两步(已标出)和埃氏筛不同,注意一下即可
最终效果:zhi数组里面全是质数,vis数组里面为true的都不是质数,既方便取质数,又方便判断质数。
下面是练习题
题目:质数率
题意:求1~n的质数占比(n<=1e8)
(这道题还是很友好的,直接让你精确,而不是求逆元,哈哈哈哈哈)
#include <bits/stdc++.h>
using namespace std;
const int N=1e8+7;
int zhi[N],cnt,m;
bool vis[N];//千万不要用int来充当bool了,内存直接超256M了!!!
int getzhi(int n){
for(int i=2;i<=n;i++){
if(!vis[i])zhi[cnt++]=i; //如果你这里想用++cnt,那么后面的j应该从1开始
for(int j=0;zhi[j]*i<=n;j++){
vis[zhi[j]*i]=true;
if(i%zhi[j]==0)break;
}
}
return cnt;
}
int main(){
cin>>m;
getzhi(m);
printf("%0.3lf\n",(double)cnt/m);
}
题目:不喜欢的数
我们不喜欢7的倍数;数字的某一位是7,这个数字的倍数我们也不喜欢。给t个数,如果这个数不是喜欢的数就输出下一个喜欢的数
思路:
注意到一个含7的数的倍数也不行,很明显我们倒着找的话需要找所有的因数来判断,但是t太大了,这样必然超时。只能正着来做!
线性筛思想O(n):如果此数喜欢,那就加入数组;否则就把此数的倍数全部筛掉
注意到要输出不喜欢数的下一个喜欢的数。对于这种取一个数的后一个数,那就定义一个链表呗(就是跟踪数组嘛)里面存放下标可以,直接存放那个数也可以,感觉你直接存那个数的话更好!
#include <bits/stdc++.h>
using namespace std;//如果是喜欢的数,就输出下一个喜欢的数(大于次数的下一个喜欢的数)(t<=2e5 x<=1e7)
const int N=1e7+7;
int t,x,ans[N],nxt[N],cnt;
bool judge[N]={1};
bool check(int x){
while(x){
if(x%10==7)return true;
x/=10;
}
return false;
}
void getnum(int n){//线性筛思想
int cur=1;//cur是上个喜欢的数,此时是第一个喜欢的数
for(int i=2;i<=n;i++){
if(!judge[i]){//忽略被筛掉的数
bool f=check(i);
if(!f){//喜欢
ans[cnt++]=i;//放入数组,感觉此步骤有点多余
nxt[cur]=i;//更新链表,里面存入这个数的下个数
cur=i;//更新cur
}else{
for(int j=i;j<=n;j+=i)//线性倍增的结果都标记一下(都是不喜欢的数)
judge[j]=true;
}
}
}
}
int main(){
getnum(N);//先对所有范围内的数都打下表格
cin>>t;
while(t--){
cin>>x;
if(judge[x]) cout<<-1<<'\n';//不喜欢则直接输出-1
else cout<<nxt[x]<<'\n';//喜欢则输出这个数的下一个数
}
return 0;
}