话不多说,直接看题:
1.辗转相减法

我们不妨假设原等比数列a,a*(q/p),a*(q/p)^2....
那么x1,,,,xn就是其中的n项,xi/x1=(q/p)^b,假设最大比例为(q/p)^k,,那么一定有(q/p)^(k*s)=(q/p)^b,即k是b的因子,这样子问题就成了求b1,...bn的gcd,那么我们如何求?
我们直接求b的gcd?但是我们知道(q/p)^b但不知道里面各个量是多少,因此无法求。
我们不妨先拆成q^b/p^b,就是求q^b的gcd,我们令f[q^b1][q^b2]=q^(b1,b2).
由(a,b)=(b,a-b)知f[q^b1][q^b2]=f[q^b2][q^b1/q^b2],这样递推即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=110;
int n;
LL a[N],b[N],x[N];
LL gcd(LL a,LL b){
return b ? gcd(b,a%b) : a;
}
LL gg(LL a,LL b){
if (a < b) swap(a, b);
if (b == 1) return a;
return gg(b, a / b);
}
int main(){
cin>>n;
for(int i=0;i<n;i++) cin>>x[i];
sort(x,x+n);
int cnt=0;
for(int i=1;i<n;i++){
if(x[i]==x[i-1]) continue;
LL d=gcd(x[i],x[0]);
a[cnt]=x[i]/d;
b[cnt]=x[0]/d;
cnt++;
}
LL up=a[0],down=b[0];
for(int i=1;i<cnt;i++){
up=gg(up,a[i]);
down=gg(down,b[i]);
}
cout<<up<<"/"<<down;
}2.扩展欧几里得:

转化一下就是:
解最小的正数x,xC-y*2^k=B-A
我们记C=a,2^k=b,那么x=x0+k*b/d;
这样我们把值%b/d+b/d即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL exgcd(LL a,LL b,LL &x,LL &y){
if(b==0){
x=1,y=0;
return a;
}
LL d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
int main(){
LL a,b,c,k;
while(cin>>a>>b>>c>>k,a||b||c||k){
LL x,y;
LL z=1ll<<k;
LL d=exgcd(c,z,x,y);
if((b-a)%d) cout<<"FOREVER"<<endl;
else{
x*=(b-a)/d;
z/=d;
cout<<(x%z+z)%z<<endl;
}
}
}3.递归

a|b表示选a或选b,括号即定义顺序,我们令&表示相连。
我们先看一下递归树,对于样例,有:

下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int k;
string s;
int dfs(){
int res=0;
while(k<s.size()){
if(s[k]=='('){
k++;
res+=dfs();
k++;//跳过)
}
else if(s[k]=='|'){
k++;
res=max(res,dfs());
}
else if(s[k]==')') break;
else{
res++;
k++;
}
}
return res;
}
int main(){
cin>>s;
cout<<dfs();
}4.重复覆盖问题:

先形象一下:
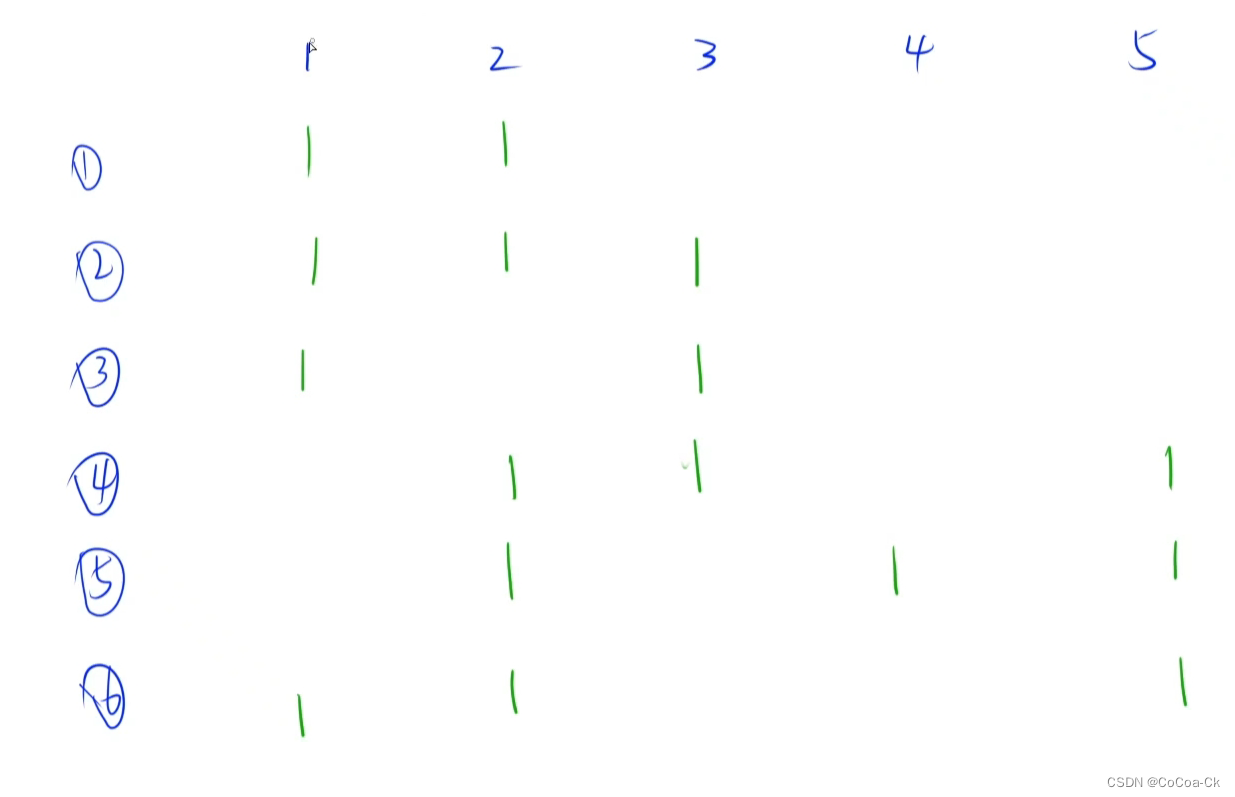
我们先看1,1要被覆盖,必选1,2,3,6(至少选一个),然后我们就枚举递归
我们考虑一下优化:
1.迭代加深:枚举下答案(答案1行不,不行的话2可以吗?)
2.我们先枚举选择最少的点(如4,只有5满足)
3.可行性剪枝:
先判断一下最少还要多少(相当于在1时把1236全选),将他与剩余的行数比较
4.位运算
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=110,M=1<<20;
int n,m,k;
vector<int> col[N];//每一列包含哪几行
int logg2[M];
int lowbit(int x){
return x&-x;
}
int h(int state){//最少几行
int res=0;
for(int i=(1<<m)-1-state;i;i-=lowbit(i)){
int c=logg2[lowbit(i)];
res++;
for(auto row:col[c]) i&=~row;
}
return res;
}
bool dfs(int dep,int state){
if(!dep||h(state)>dep) return state==(1<<m)-1;//只有state满时才可能
//找到选择min
int t=-1;
for(int i=(1<<m)-1-state;i;i-=lowbit(i)){
int c=logg2[lowbit(i)];
if(col[c].size()<col[t].size()||t==-1) t=c;
}
for(auto row:col[t]){
if(dfs(dep-1,state|row)) return 1;
}
return 0;
}
int main(){
cin>>n>>m>>k;
for(int i=0;i<m;i++) logg2[1<<i]=i;
for(int i=0;i<n;i++){
int state=0;
for(int j=0;j<k;j++){
int c;
scanf("%d",&c);
state|=1<<(c-1);
}
for(int j=0;j<m;j++){
if(state>>j&1){
col[j].push_back(state);
}
}
}
for (int i = 0; i < m; i ++ )
{
sort(col[i].begin(), col[i].end());
col[i].erase(unique(col[i].begin(), col[i].end()), col[i].end());//unique把重复元素放后,返回第一个重复的迭代器;
}
int dep=0;
while(dep<=m&&!dfs(dep,0)) dep++;//迭代加深,层数就是选的糖果数
if(dep>m) dep=-1;
cout<<dep;
}