我们之前学习了搜索二叉树,我们知道普通的搜索二叉树会有特殊情况出现使得二叉树的两枝极其不平衡形成我们通俗说的歪脖子树:

这样的树一定会使得我们的增删查的效率变低;为了避免这种极端的情况出现,在1962年有两位伟大的俄罗斯数学家Adelson-Velsky和Landis发明的;它们通过旋转使得我们的树的任意节点的左右子树高度差不超过2;使得搜索二叉树总会是一颗平衡的搜索二叉树;
我们怎么知道我们的左右子树的高度差呢?
AVL树的节点
我们这个时候就需要在搜索二叉树的基础上对我们的节点进行修改了,给我们的节点增加一个平衡因子_balance factor(_bf);
_bf平衡因子
介绍_bf:
_bf是如何计算的呢?创作者规定 _bf=右子树的深度-左子树的深度; 也就是说,我们每次我们插入一个新节点到我们当前节点的左边的时候_bf需要减一,当新节点插入到我们当前节点的右边的时候_bf加一;

template<class K,class V>
struct AVLTreeNode
{
typedef AVLTreeNode<K,V> node;
node* _left;
node* _right;
node* _parent;
pair<K,V> _data;
int _bf;//balance factor平衡因子
AVLTreeNode(const pair<K, V>& data)
:_left(nullptr)
, _right(nullptr)
,_parent(nullptr)
,_data(data)
,_bf(0)
{}
};可以看到,我们的AVL树的成员增加了_bf平衡因子和_parent父亲节点的指针;
有了描述每个节点的条件,要开始组织起来这些节点了,我们需要插入一个个节点;
插入节点
一开始插入节点是与搜索二叉树相同,我们需要先找到节点插入的位置,然后再将新增节点连接到我们的原树的叶子节点的末端,这个时候插入就完成了;
不同的是插入完成后,我们需要更新我们父亲节点的_bf平衡因子;采用上方所说的插入位置在父亲节点左侧时,父亲节点_bf-1,插入在父亲节点右侧时当前节点_bf+1;更新完成父亲节点后向上不断遍历修改父亲的父亲节点;而这个遍历我们又需要分情况遍历;
插入操作(和搜索二叉树中操作相同)
if (_root == nullptr)
{
_root = new node(data);
return true;
}
node* cur = _root;
node* parent = _root;
while (cur)
{
if (data.first < cur->_data.first)
{
parent = cur;
cur = cur->_left;
}
else if (data.first > cur->_data.first)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new node(data);
cur->_parent = parent;
if (data.first < parent->_data.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
以上是普通的插入操作,下面需要进行平衡因子更新更新_bf
情况1:父亲节点的_bf更新为1或-1
如果父节点的_bf为1或者1时就代表我们的父节点的左边或者右边新插入了节点,我们我们当前父节点为根的子树高度增加了,从而我们又会影响到父亲节点的父亲节点;所以我们需要继续所以向上遍历让父亲节点成为新插入的节点,更新父亲节点的父亲节点成为parent(父亲),更新新的父亲的_bf;

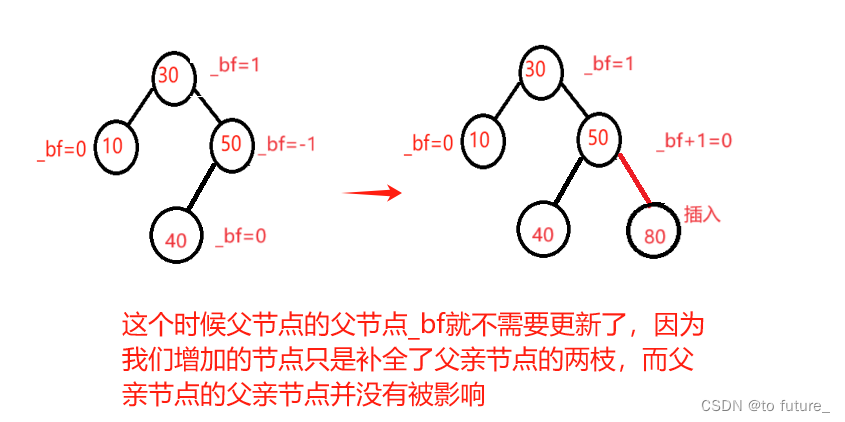
情况2:父亲节点的_bf更新为0
此时说明我们的父亲节点为根节点的树原本是不平衡的,但是由于我们插入的新节点补齐了这颗树;使得父亲节点的_bf变为了0,这个时候由于父亲节点为根的树高度没有变化;所以父亲节点上层的节点自然也不需要更新_bf所以这个时候可以直接退出遍历了;
情况3:父亲节点的_bf绝对值大于1
这个时候,我们需要进行旋转来降低父节点为根的树高度了
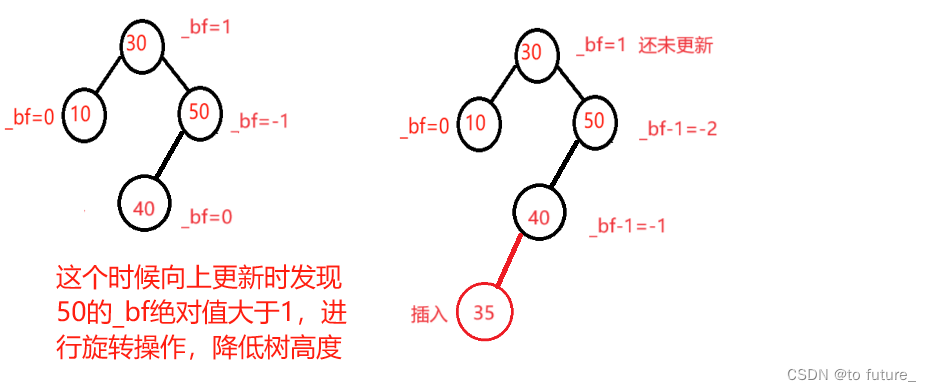
循环向上更新_bf
while (parent)
{
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
if (parent->_bf == 1 || parent->_bf == -1)//-1or1时需要继续更新平衡因子
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 0)//因子为0是将树补齐了不需要再向上更新了
{
break;
}
else if (parent->_bf == 2 || parent->_bf == -2)//2or-2时需要旋转减小树的高度
{
if (parent->_bf == -2 && parent->_left->_bf == -1)//左子树的左子树高右旋转
{
RotateR(parent);
}
else if (parent->_bf == 2 && parent->_right->_bf == 1)//右子树的右子树高左旋转
{
RotateL(parent);
}
else if (parent->_bf == -2 && parent->_left->_bf == 1)//左子树的右子树高,先右子树左旋再左子树右旋
{
RotateLR(parent);
}
else if (parent->_bf == 2 && parent->_right->_bf == -1)//右子树的左子树高,先左子树右旋再右子树左旋
{
RotateRL(parent);
}
else
{
assert(false);
}
break;
}
}旋转
这个操作就是AVL最精华的部分了;我们知道是当树左右两边高度相差超高1的时候就需要旋转了;旋转主要是靠画图理解;
我们需要注意的是我们旋转的树是一般是子树(父节点为根时为整棵树);
而旋转又分为四种旋转情况:
为了方便描述我们将当前树的根节点同一叫根节点;
单旋
情况1:根节点_bf为-2根节点左节点_bf为-1时(右单旋)
当根节点_bf为-2时说明我们这棵树的左子树高度要比右子树高2个节点的高度,根左节点的_bf为-1又说明我们左子树的左子树比左子树的右子树高1个节点的高度,也就是如下图:
我们需要进行单旋,因为是左树高,所以需要进行右旋转,将根节点旋转为左节点的右节点
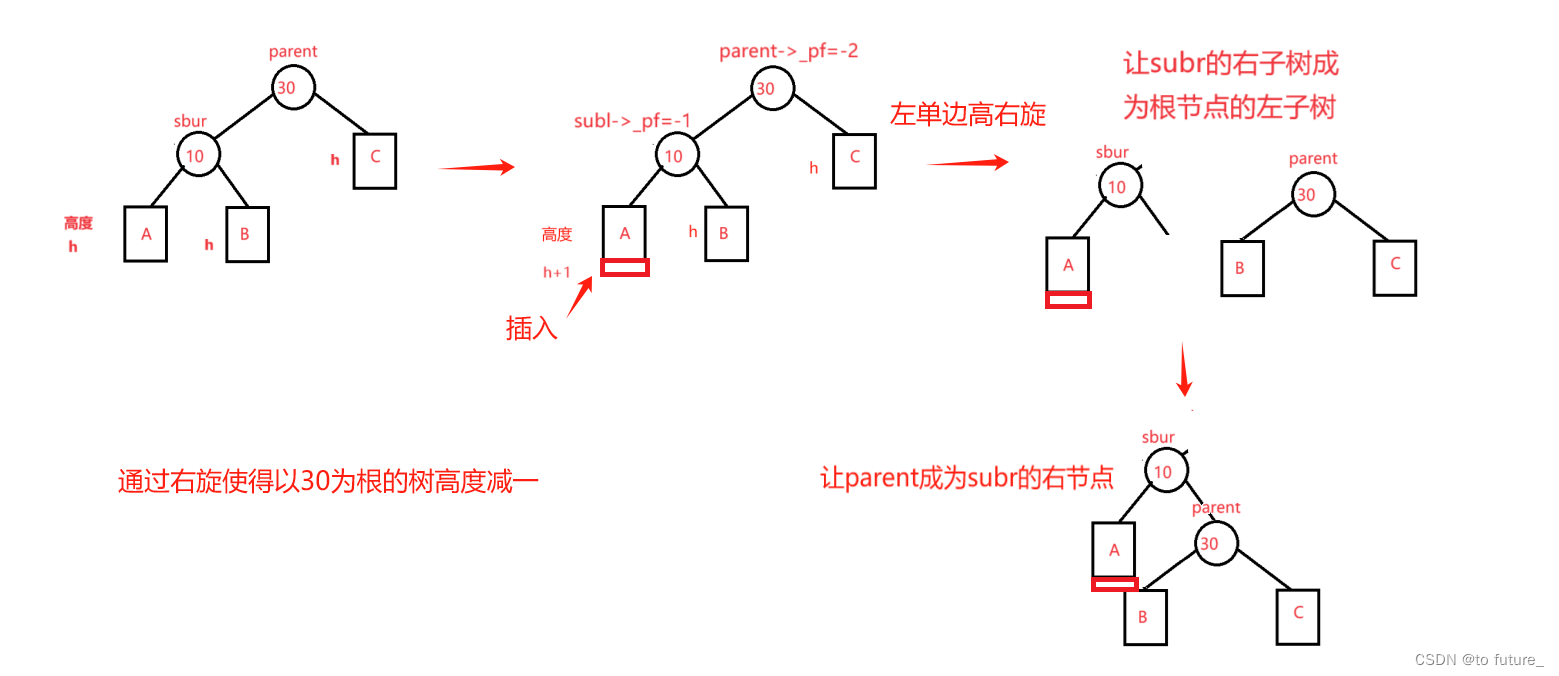
右单旋
void RotateR(node* parent)
{
node* subl = parent->_left;
node* sublr = subl->_right;
parent->_left = sublr;
if (sublr)
sublr->_parent = parent;
node* ppnode = parent->_parent;
subl->_right = parent;
parent->_parent = subl;
if (ppnode == nullptr)
{
_root = subl;
_root->_parent = nullptr;
}
else
{
subl->_parent = ppnode;
if (ppnode->_left == parent)
{
ppnode->_left = subl;
}
else
{
ppnode->_right = subl;
}
}
parent->_bf = subl->_bf = 0;
return;
}情况2:根节点_bf为2根节点右节点_bf为1时(左单旋)
这种情况就是情况1的对立边,这次是右树的右子树高,我们需要进行左单旋;
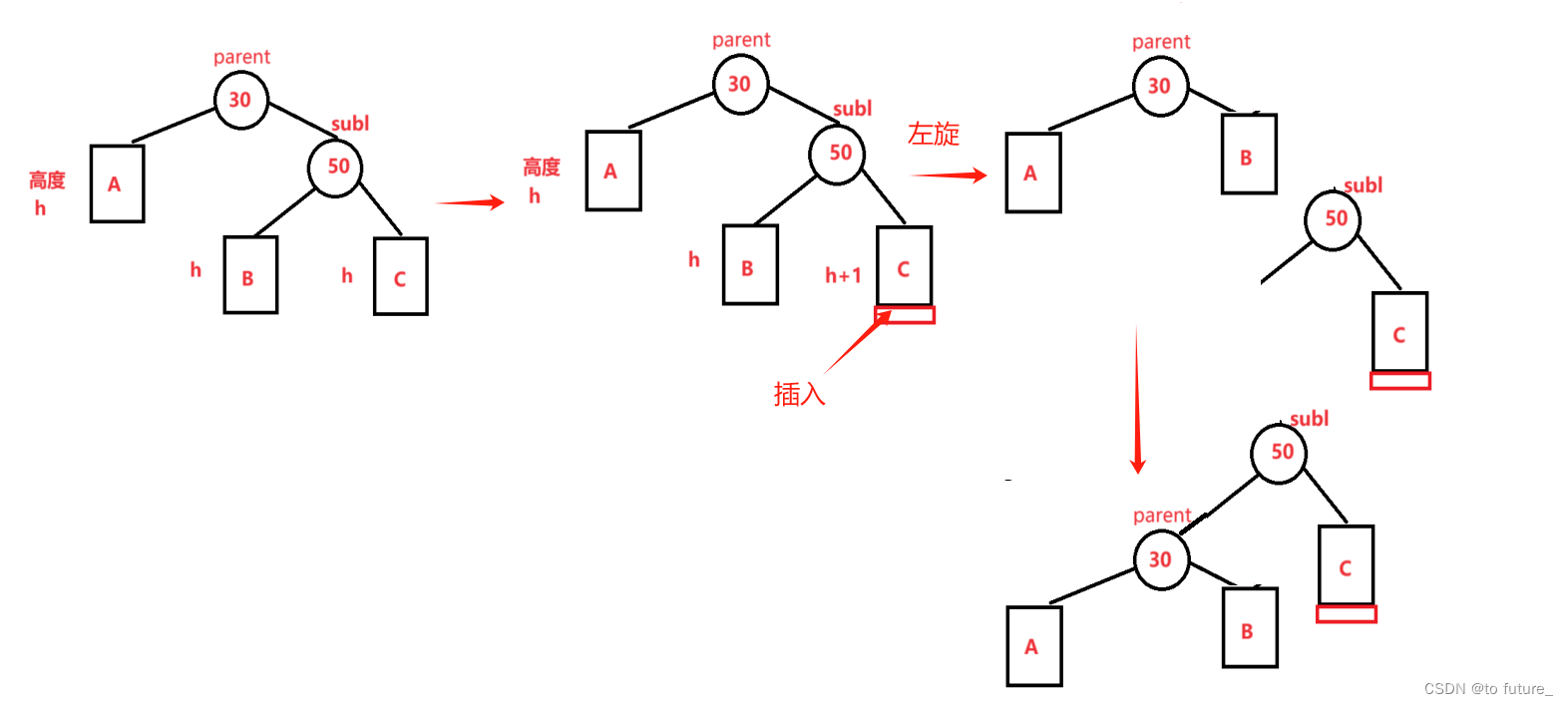
左单旋
void RotateL(node* parent)
{
node* subr = parent->_right;
node* subrl = subr->_left;
parent->_right = subrl;
if (subrl)
subrl->_parent = parent;
node* ppnode = parent->_parent;
subr->_left = parent;
parent->_parent = subr;
if (ppnode == nullptr)
{
_root = subr;
_root->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subr;
}
else
{
ppnode->_right = subr;
}
subr->_parent = ppnode;
}
parent->_bf = subr->_bf = 0;
}单旋之后我们的parent和左节点的_pf都为0;
双旋
情况3:根节点_pf为-2根节点的左节点_pf为1(左右双旋)
这种情况就是我们的根节点左树高,但左数中的右树高,我们需要进行双旋:
如何左右双旋如图:
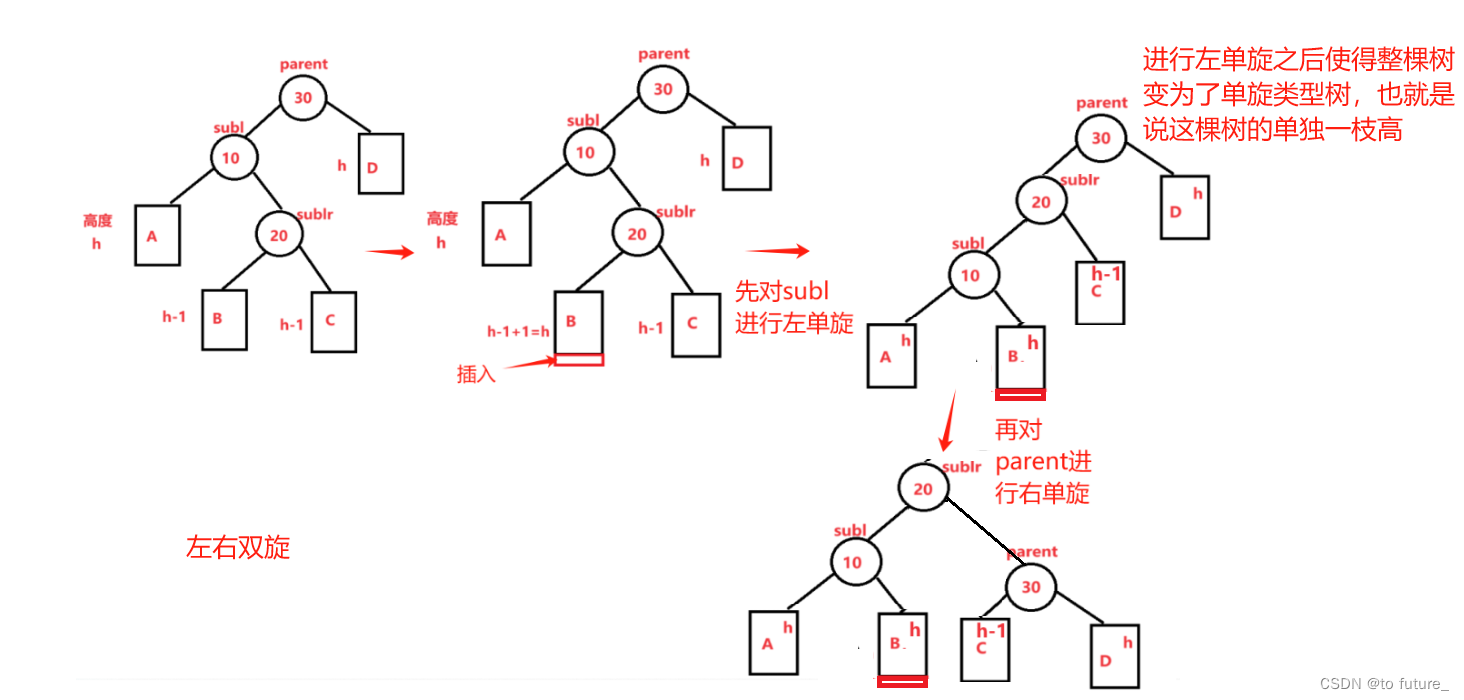
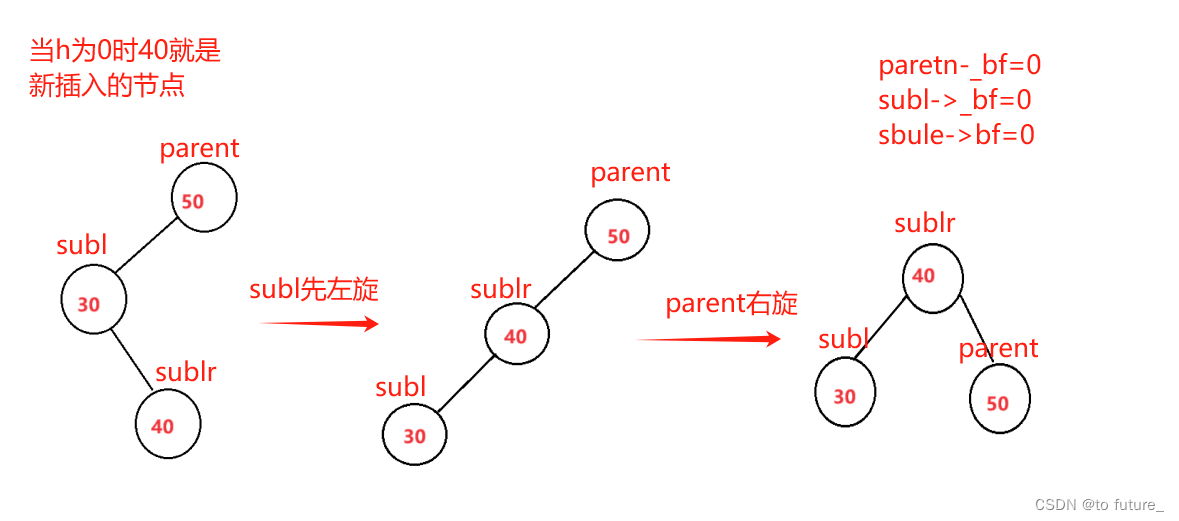
值得注意的是双旋我们的_bf是需要更新的;我们需要通过sublr的_bf来判断更新值
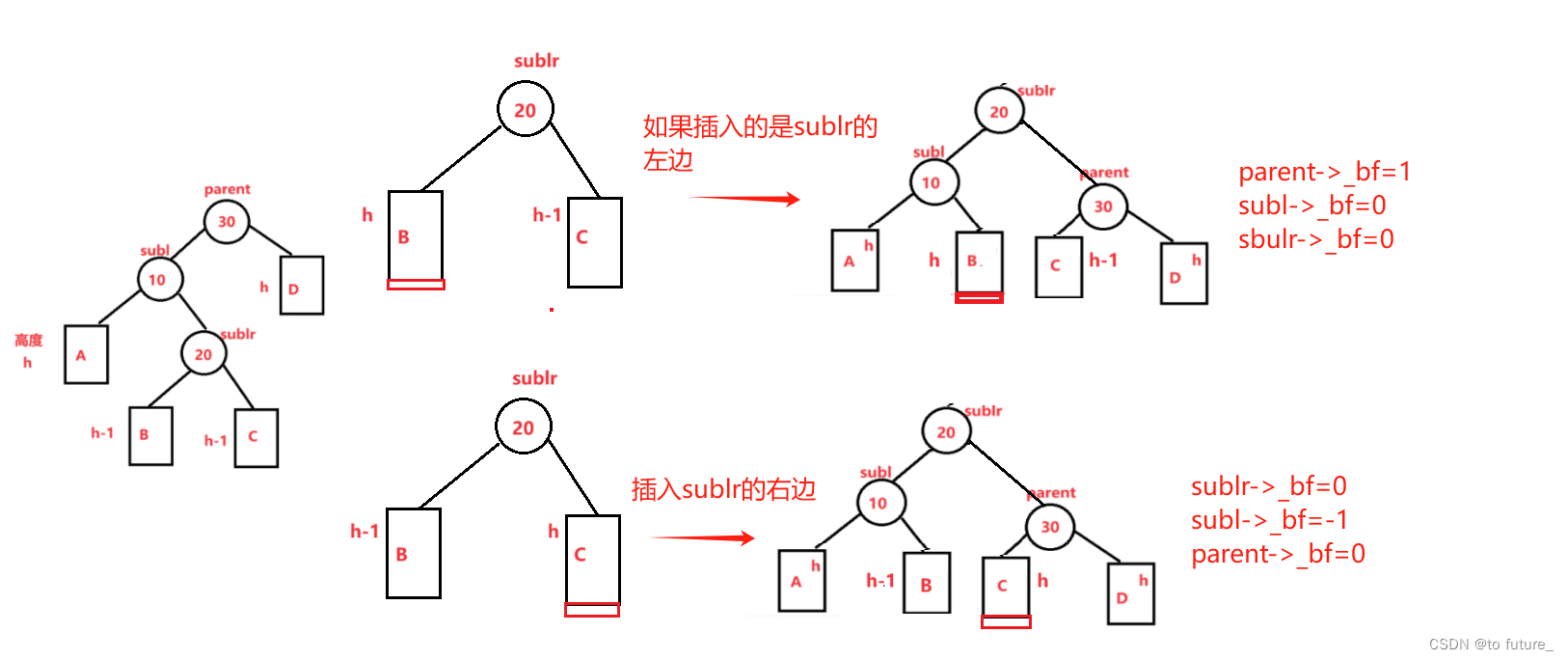
代码实现
void RotateLR(node* parent)
{
node* subl = parent->_left;
node* sublr = subl->_right;
int flag = sublr->_bf;
RotateL(subl);//左旋右子树(树中树)
RotateR(parent);//右旋左子树
//更新平衡因子
if (flag == 1)//插入位置为树中树的右树
{
parent->_bf = 0;
subl->_bf = -1;
sublr->_bf = 0;
}
else if (flag == -1)
{
parent->_bf = 1;
subl->_bf = 0;
sublr->_bf = 0;
}
else if (flag == 0)
{
parent->_bf = 0;
subl->_bf = 0;
sublr->_bf = 0;
}
else
{
assert(false);
}
}情况4:根节点_pf为2根节点的右节点_pf为-1(右左双旋)
此情况就是不同与单旋时的单一枝高,而是一枝中的另一枝高;
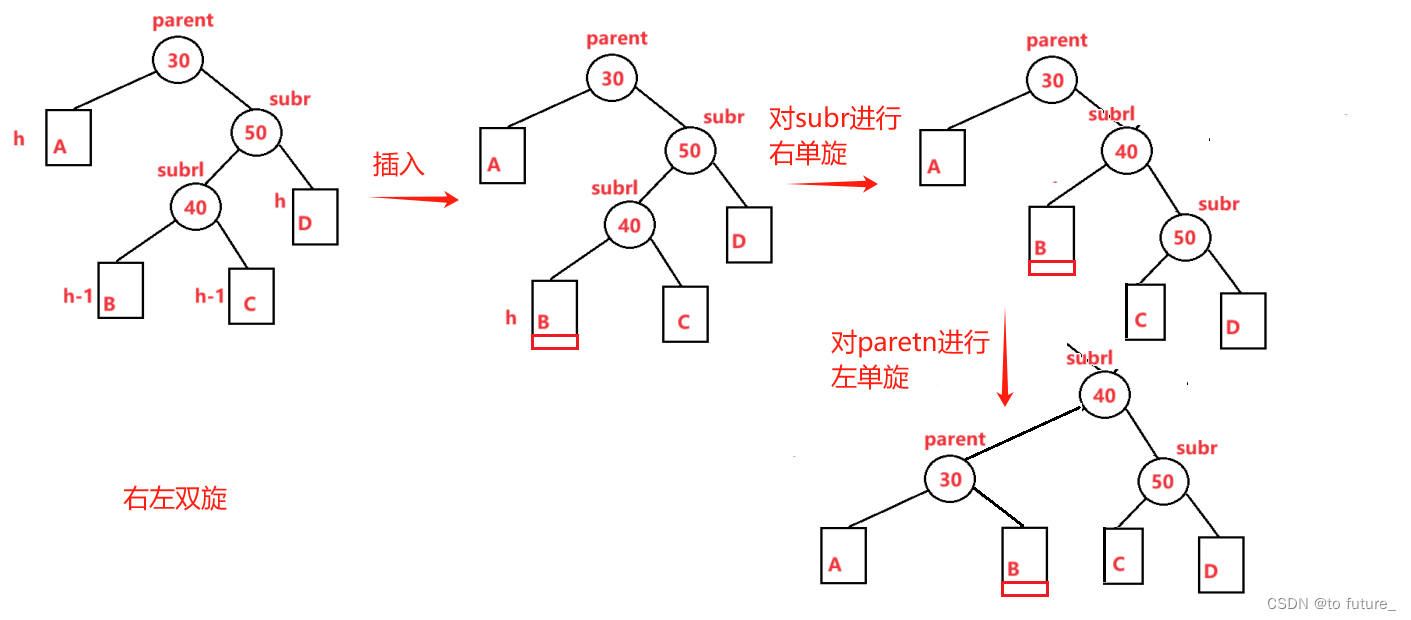
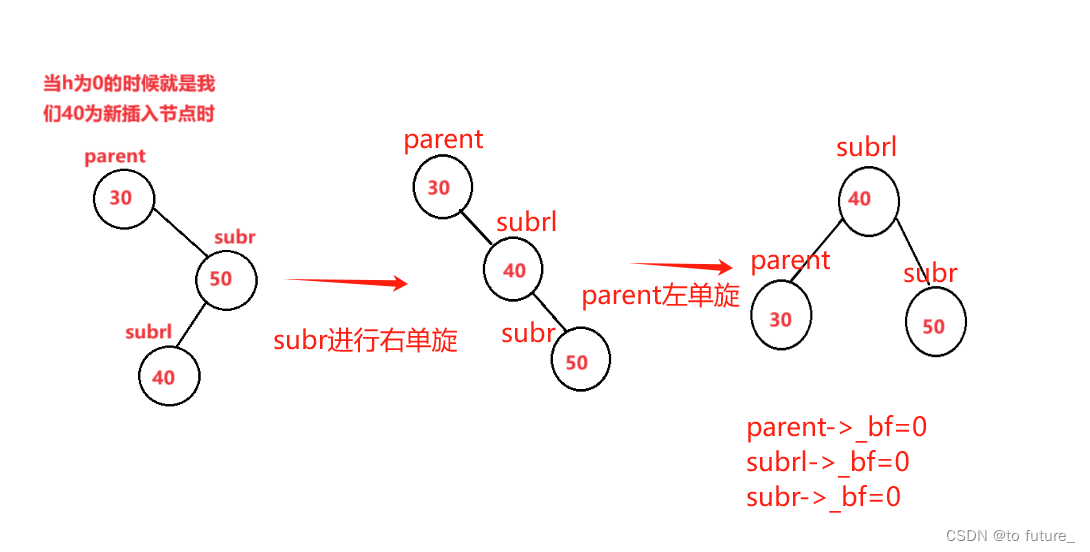
同样的我们旋转之后更新我们的_bf;
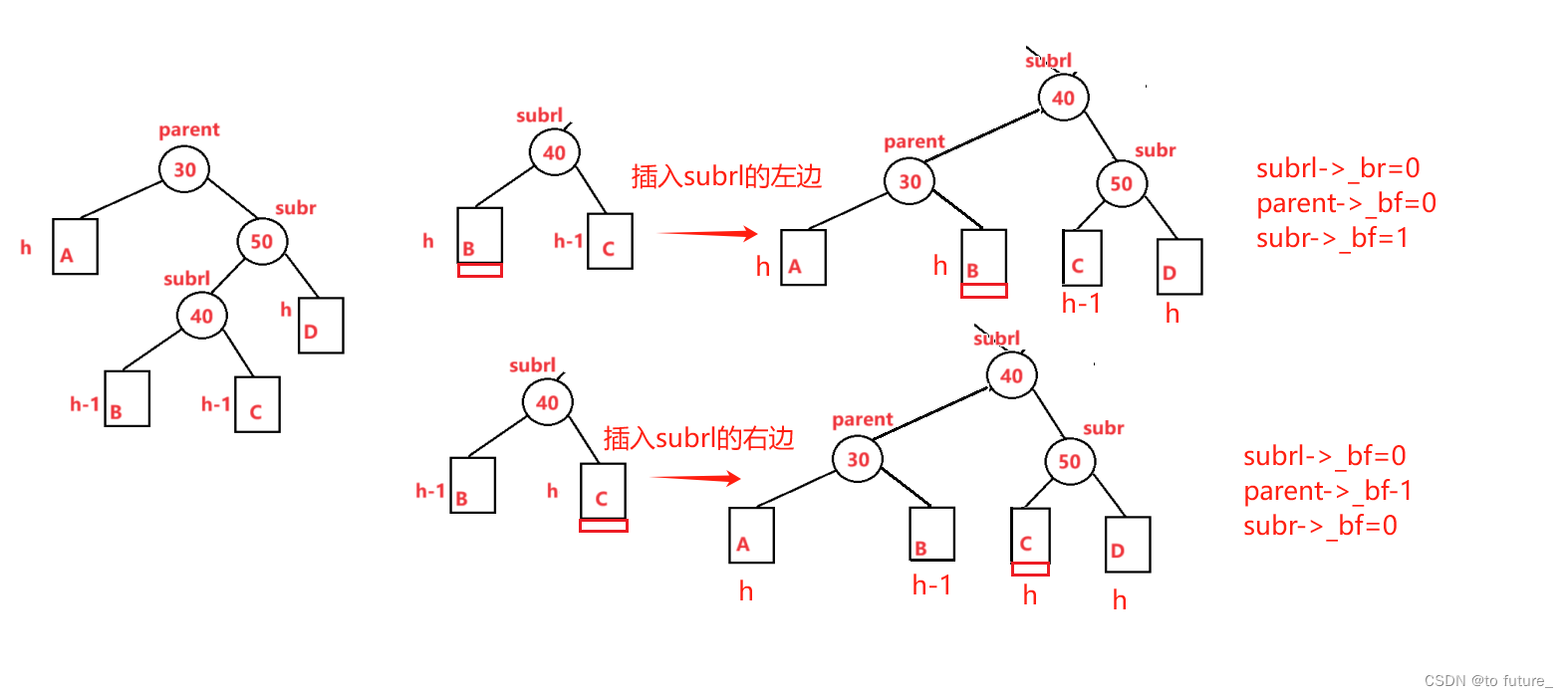
代码实现
void RotateRL(node* parent)
{
node* subr = parent->_right;
node* subrl = subr->_left;
int flag = subrl->_bf;
RotateR(subr);//右旋左子树(树中树)
RotateL(parent);//左旋右子树
//更新平衡因子
if (flag == 1)//插入位置为树中树的右树
{
parent->_bf = -1;
subr->_bf = 0;
subrl->_bf = 0;
}
else if (flag == -1)
{
parent->_bf = 0;
subr->_bf = 1;
subrl->_bf = 0;
}
else if (flag == 0)
{
parent->_bf = 0;
subr->_bf = 0;
subrl->_bf = 0;
}
else
{
assert(false);
}
}当上面的旋转和更新_bf都完成的时候,这棵树我们插入就一定是我们的AVL树了;
为了验证我们的树是否真的成为了AVL树我们需要通过检查算法来比较每个节点的_bf是否正确
void _print(node* root)
{
if (root == nullptr)
return;
_print(root->_left);
cout << root->_data.first << " ";
_print(root->_right);
}
bool judgeBalance()
{
return _judgeBalance(_root);
}
bool _judgeBalance(node*root)
{
if (root == nullptr)
return true;
int hl = getDeep(root->_left);//hightLeft
int hr = getDeep(root->_right);//hightRight
int judge = hr - hl;
if (judge != root->_bf)
{
cout << root->_data.first << "这个节点的_pf没处理好" << endl;
return false;
}
return _judgeBalance(root->_left) && _judgeBalance(root->_right);
}
void testAVLTree1()
{
AVLTree<int, int>t;
srand(time(0));
for (int i = 0; i < 100; i++)
{
int x = rand();
t.insert(make_pair(x, x));
}
t.print();
cout << t.judgeBalance() << endl;
}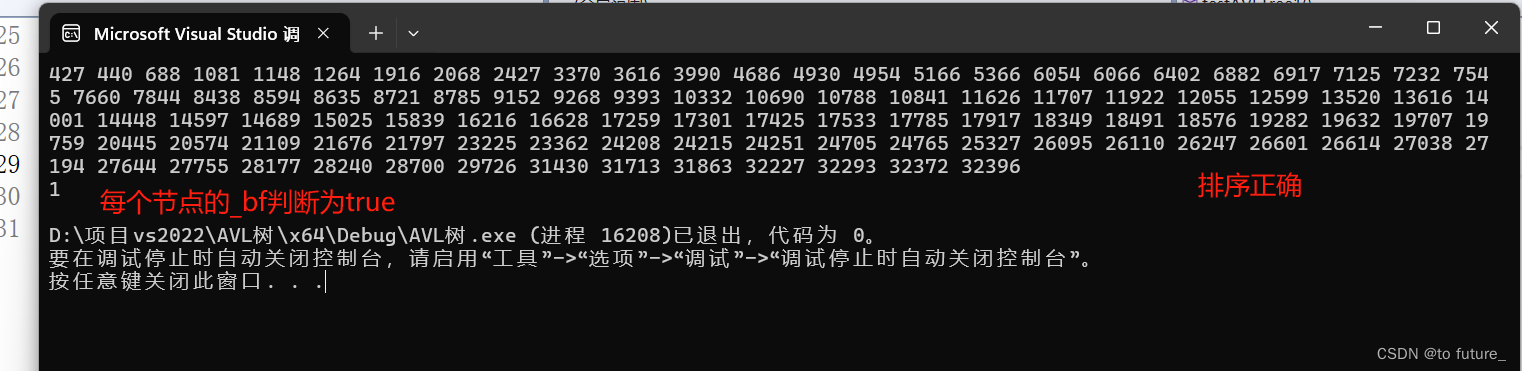
此时我们的树就是一颗完全正确的AVL树 ;
我们只实现了AVL树的插入算法,删除算法还没有学习;
这是我的完整的AVL树代码:
C++代码/AVL树 · future/my_road - 码云 - 开源中国 (gitee.com)