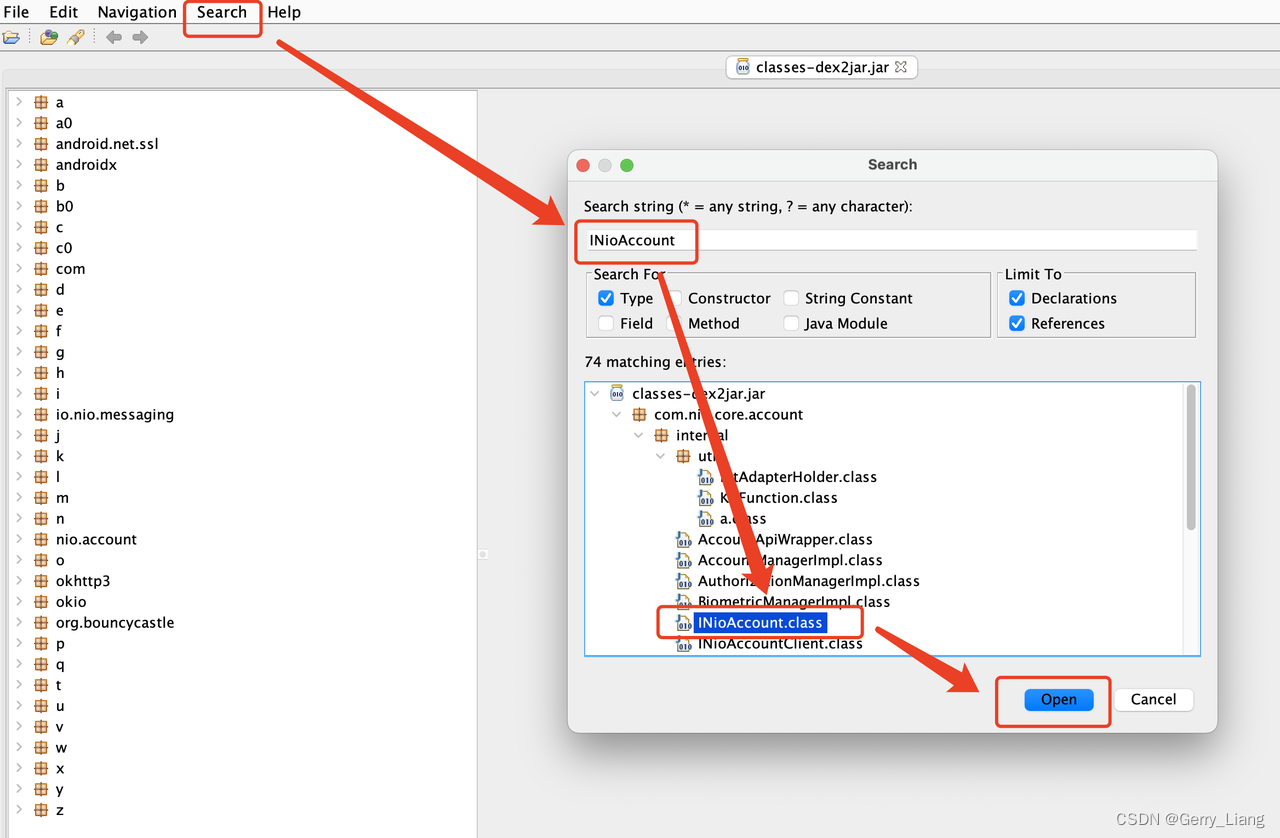
题目链接

CodeTON Round 8 (Div. 1 + Div. 2, Rated, Prizes!)

C2. Bessie’s Birthday Cake (Hard Version)

---

思路：

其实可以先做一下easy version。

先不选点，已有的点我们肯定能加多少边就加多少，而且手玩后发现一个规律，就是不管我们怎么加边，总的加边数量和产生的三角形个数是固定的，只和点的个数有关。点的个数-2=三角形个数。

我们把已有的点的外围边画出来，这就相当于一个多边形，多边形内部已经拆出了足够多的三角形，我们不需要管了，看外部剩下的边角料。

手玩几个发现一个规律，那就是剩下的这个 $n+2$ 边形，两个点我们已有，剩下的点每隔一个点选一个点，一下可以拆出两个三角形（大概如下图，绿色点已有，黄色点是选择的点），剩下的部分同理接着向下拆。不过最后收尾的时候，如果 $n=1$，就不需要切了，剩下的直接就是一个三角形，如果 $n=2$，还需要选一个点。

这样，一个 $n+2$ 边形选择 $\lfloor \frac{n}{2}\rfloor$ 个点，可以切成 $n$ 个三角形。

这样，我们选一个点至少可以得到两个三角形，而且当 $n$ 为奇数时，我们收尾的时候还可以白嫖一个三角形。因此我们优先贪心地去切边数较小的奇数边多边形，这样得到三角形的个数就是最多的。反正切一刀固定得到两个三角形，在这个基础上尽可能多的白嫖即可。

code：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;

int T,n,x,y,a[maxn];
ll ans=0;

int main(){
	cin>>T;
	while(T--){
		cin>>n>>x>>y;
		ans=max(0,x-2);
		for(int i=1;i<=x;i++)cin>>a[i];
		sort(a+1,a+x+1);
		a[x+1]=a[1]+n;
		multiset<int> S1,S2;
		for(int i=2,t;i<=x+1;i++){
			t=a[i]-a[i-1]-1;
			if(t&1)S1.insert(t);
			else S2.insert(t);
		}
		
		for(auto t1:S1){
			if(y>=t1/2){
				y-=t1/2;
				ans+=t1;
			}
			else {
				ans+=2*y;
				y-=y;
				break;
			}
		}
		for(auto t2:S2){
			if(y>=t2/2){
				y-=t2/2;
				ans+=t2;
			}
			else {
				ans+=2*y;
				y-=y;
				break;
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}