基于栈结构的非递归二叉树结点关键字输出算法

一、引言
二、二叉树基本概念
三、非递归遍历算法基础
四、算法设计
五、算法实现
六、C代码示例
七、算法分析
八、优化与讨论

一、引言

在计算机科学中，二叉树是一种重要的数据结构，它广泛应用于各种算法和数据结构中。对于二叉树的遍历，通常有递归和非递归两种方法。递归方法简单直观，但在处理大型数据结构时，可能会因为递归调用栈过深而导致栈溢出。因此，非递归方法在处理大规模数据时更为稳健。本文将探讨一种使用栈作为辅助数据结构的非递归算法，用于输出二叉树每个结点的关键字。
在这里插入图片描述

二、二叉树基本概念

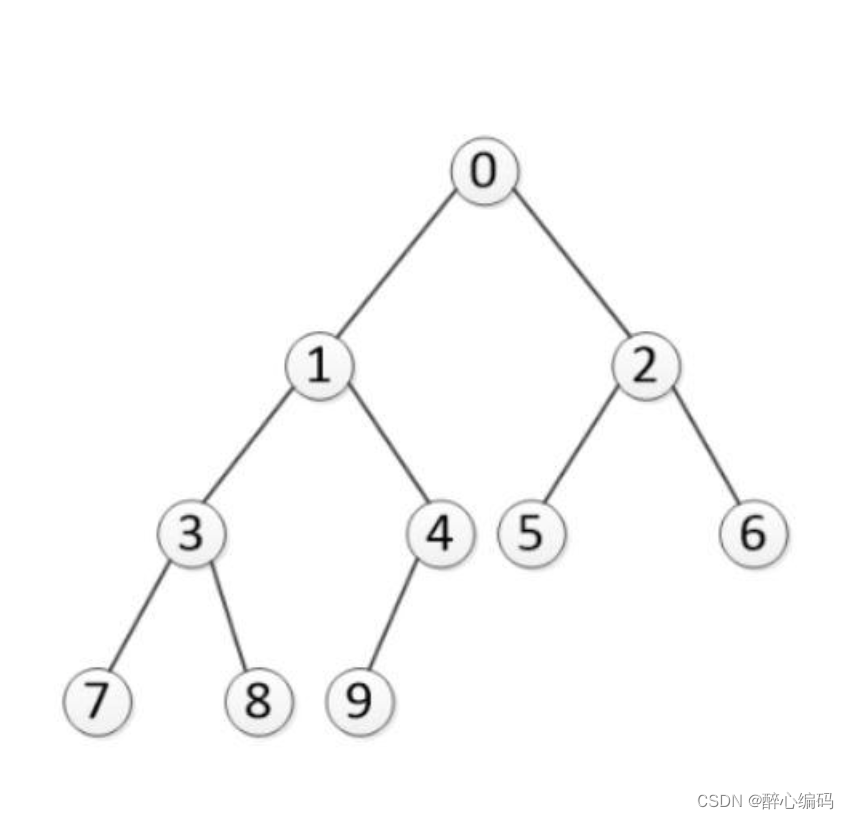
二叉树是每个结点最多有两个子树的树结构，通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。在二叉树中，一个结点通常包含一个关键字（key）和两个链接（left和right），分别指向左子树和右子树。如果某个结点没有子结点或者只有一个子结点，那么对应的链接就是空（NIL）。

三、非递归遍历算法基础

非递归遍历二叉树的关键在于如何模拟递归过程，即如何显式地维护一个“调用栈”。在递归遍历中，每次递归调用都会将当前结点的信息压入调用栈，并在返回时弹出。在非递归遍历中，我们需要使用一个显式的栈来模拟这个过程。通常，我们使用一个先进后出（LIFO）的数据结构——栈，来保存待处理的结点。

四、算法设计

以下是一个基于栈的非递归算法，用于输出二叉树每个结点的关键字：

初始化一个空栈。
将根结点压入栈中。
当栈不为空时，执行以下循环：
a. 从栈中弹出一个结点。
b. 输出该结点的关键字。
c. 如果该结点有右子结点，将右子结点压入栈中。
d. 如果该结点有左子结点，将左子结点压入栈中。
这个算法的关键在于，每次从栈中弹出一个结点时，都先处理右子结点（如果存在），再处理左子结点。这是因为栈是后进先出的数据结构，所以我们需要先压入左子结点，再压入右子结点，以保证在处理时先访问右子结点。

五、算法实现

以下是一个简单的伪代码实现：

function printTreeKeys(root):  
    if root is None:  
        return  
      
    stack = createStack()  
    push(stack, root)  
      
    while not isEmpty(stack):  
        node = pop(stack)  
        print(node.key)  # 输出结点关键字  
          
        if node.right is not None:  
            push(stack, node.right)  # 右子结点入栈  
        if node.left is not None:  
            push(stack, node.left)  # 左子结点入栈
在这个实现中，createStack 函数用于创建一个空栈，push 函数用于将元素压入栈中，pop 函数用于从栈中弹出元素，isEmpty 函数用于检查栈是否为空。这些函数的具体实现取决于你使用的编程语言和库。

六、C代码示例

以下是一个使用C语言实现的基于栈的非递归二叉树遍历算法示例。这个示例将展示如何定义一个二叉树结构，如何创建一个简单的二叉树，以及如何使用栈来进行非递归的先序遍历（根-左-右）。

#include <stdio.h>  
#include <stdlib.h>  
  
// 定义二叉树结点结构体  
typedef struct TreeNode {  
    int key;  
    struct TreeNode *left;  
    struct TreeNode *right;  
} TreeNode;  
  
// 定义栈结构体  
typedef struct Stack {  
    TreeNode *data;  
    struct Stack *next;  
} Stack;  
  
// 创建新结点  
TreeNode* createNode(int key) {  
    TreeNode *newNode = (TreeNode*)malloc(sizeof(TreeNode));  
    newNode->key = key;  
    newNode->left = NULL;  
    newNode->right = NULL;  
    return newNode;  
}  
  
// 创建栈  
Stack* createStack() {  
    Stack *newStack = (Stack*)malloc(sizeof(Stack));  
    newStack->next = NULL;  
    return newStack;  
}  
  
// 判断栈是否为空  
int isEmpty(Stack *stack) {  
    return stack->next == NULL;  
}  
  
// 入栈  
void push(Stack *stack, TreeNode *node) {  
    Stack *newStack = (Stack*)malloc(sizeof(Stack));  
    newStack->data = node;  
    newStack->next = stack->next;  
    stack->next = newStack;  
}  
  
// 出栈  
TreeNode* pop(Stack *stack) {  
    if (isEmpty(stack)) {  
        return NULL;  
    }  
    Stack *top = stack->next;  
    TreeNode *data = top->data;  
    stack->next = top->next;  
    free(top);  
    return data;  
}  
  
// 非递归先序遍历  
void preOrderTraversal(TreeNode *root) {  
    if (root == NULL) {  
        return;  
    }  
      
    Stack *stack = createStack();  
    push(stack, root);  
      
    while (!isEmpty(stack)) {  
        TreeNode *node = pop(stack);  
        printf("%d ", node->key); // 输出结点关键字  
          
        if (node->right != NULL) {  
            push(stack, node->right); // 右子结点入栈  
        }  
        if (node->left != NULL) {  
            push(stack, node->left); // 左子结点入栈  
        }  
    }  
      
    // 清理栈内存（可选，因为程序结束时会自动释放）  
    while (!isEmpty(stack)) {  
        pop(stack);  
    }  
    free(stack);  
}  
  
// 主函数  
int main() {  
    // 创建一个简单的二叉树  
    TreeNode *root = createNode(1);  
    root->left = createNode(2);  
    root->right = createNode(3);  
    root->left->left = createNode(4);  
    root->left->right = createNode(5);  
    root->right->left = createNode(6);  
    root->right->right = createNode(7);  
      
    // 执行非递归先序遍历  
    printf("Pre-order traversal: ");  
    preOrderTraversal(root);  
    printf("\n");  
      
    // 清理二叉树内存（可选）  
    // ... (此处省略了二叉树的销毁代码)  
      
    return 0;  
}

请注意，这个示例仅用于教学目的，并未包含所有可能的错误检查和内存管理最佳实践。在实际应用中，你应该更加注意内存泄漏和错误处理。例如，在销毁二叉树时，你需要递归地释放每个结点的内存。同样地，在处理栈时，你也需要确保在不再需要时释放栈所占用的内存。在这个简单的示例中，我省略了这些步骤以保持代码的简洁性。