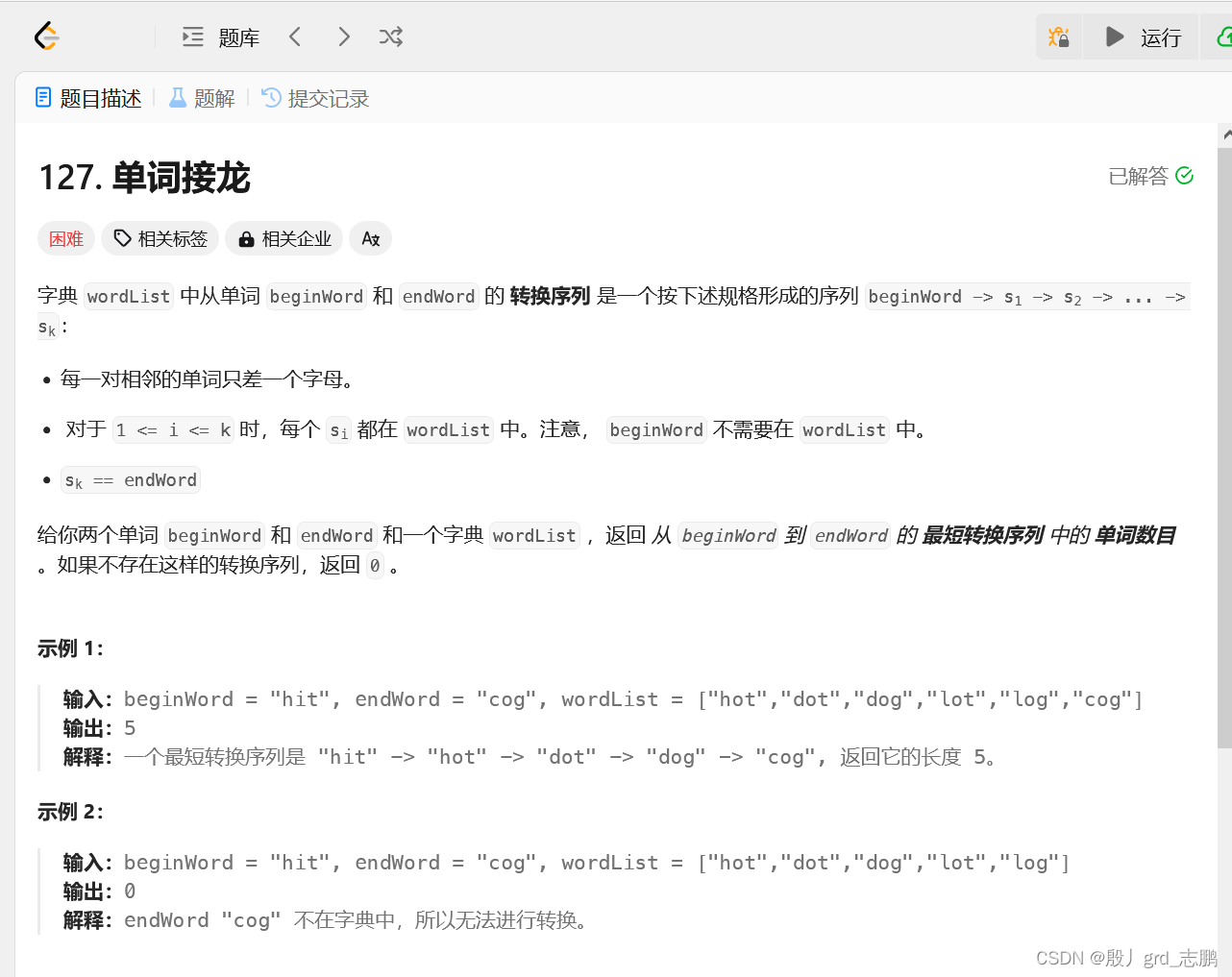
java数据结构与算法刷题目录（剑指Offer、LeetCode、ACM）-----主目录-----持续更新(进不去说明我没写完)：https://blog.csdn.net/grd_java/article/details/123063846

广度优先+双分裂蛇

解题思路：时间复杂度O($n\ast c\ast 26$),n是字典中单词个数，c是单词的长度，26是26个字母，空间复杂度O($n\ast c\ast 26$)

1. 此题就是求二维图起点到终点的最短路径问题。而这个问题本身只是中等难度。但是为什么这道题是困难难度呢？因为这道题太抽象了，虽然是考查图的最短路径，但是题目描述很难让人联想到图，所以以后只要遇到求最短路径的题，看看能不能抽象成二维图，能就说明考察的分裂蛇知识点。
2. 这道题只要抽象成图的数据结构，就退化为1091题了,只要1091题掌握了，这道题就只需要你将图的逻辑抽象出来就可以了。不过这道题的处理稍微有些不同.

如果不清楚什么是双分裂蛇，1091题都有详细的介绍

🏆LeetCode1091. 二进制矩阵中的最短路径https://blog.csdn.net/grd_java/article/details/137090602

3. 将题目给的字典中每个单词都抽象成一个顶点，而两个单词如果只有一个字母不一样，就抽象成这两个单词之间有一条边。这样就有了图数据结构了。
4. 然后创建两个Set集合（一般是用队列，但是这道题用队列反而不太好做，因为我们需要确定当前A队列遇到的新单词是否在另一个队列中）。一个从头开始走，一个从终点开始走。

5. 因为我们是抽象的图数据结构，不知道顶点和边的关系，所以我们需要每遇到一个单词，就替换它里面每个字母生成一个新单词，只要这个新单词是题目所给字典中的单词，就说明当前这个单词和这个新单词都是存在于字典中的，且两者之间有一条边。因此这些新单词就是当前结点的下一个广度优先遍历对象

因为两个单词如果只有一个字母不一样，就抽象成这两个单词之间有一条边,但是题目本身没给这个关系，我们只能一个个枚举（修改这个单词中单个字母），时间复杂度是O($c\ast 26$),c是这个单词由几个字母组成

6. 当首尾两个集合相遇的一瞬间，其代表的路径就是最短路径（双分裂蛇的特点）。

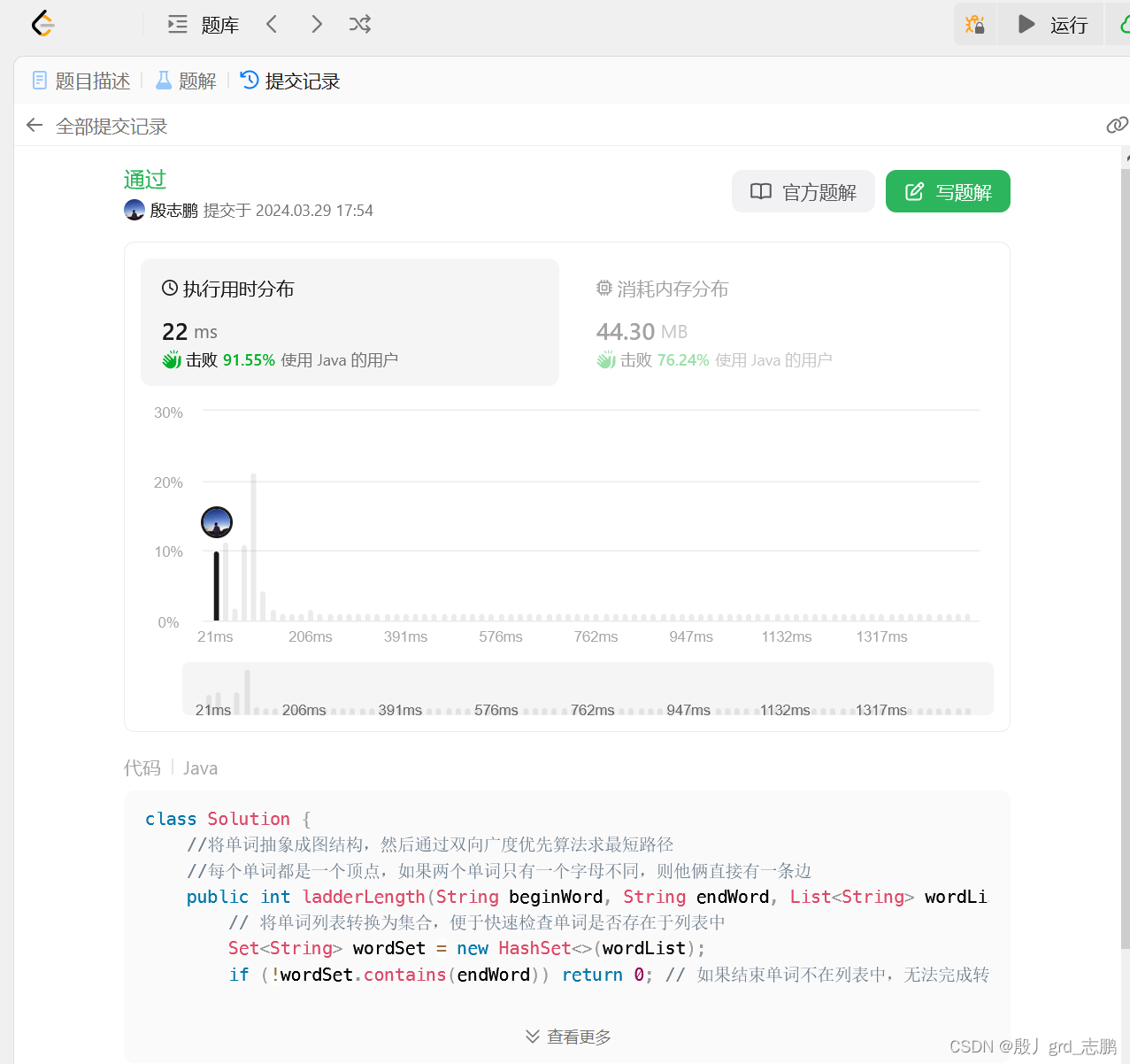
代码：官方增加了测试用例，相同的算法原来是21ms超越100%，现在只能到达22ms，已经无法超越100%了

class Solution {
    //将单词抽象成图结构，然后通过双向广度优先算法求最短路径
    //每个单词都是一个顶点，如果两个单词只有一个字母不同，则他俩直接有一条边
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        // 将单词列表转换为集合，便于快速检查单词是否存在于列表中
        Set<String> wordSet = new HashSet<>(wordList);
        if (!wordSet.contains(endWord)) return 0; // 如果结束单词不在列表中，无法完成转换，直接返回0

        // 使用两个集合（代替队列）分别存储从开始和结束单词出发的广度优先搜索的边界。双向广度优先，一个从起点，一个从终点找
        Set<String> beginSet = new HashSet<>(), endSet = new HashSet<>();
        int len = 1; // 初始化路径长度为1，因为开始单词也计入路径
        int strLen = beginWord.length(); // 单词的长度，假设所有单词长度相同
        HashSet<String> visited = new HashSet<>(); // 记录已访问的单词，避免重复处理，我们不更改原表，使用新的表来标志某个单词是否已经访问

        // 将开始和结束单词加入对应的集合
        beginSet.add(beginWord);
        endSet.add(endWord);
        // 只要两个集合都非空，就继续执行双向搜索
        while (!beginSet.isEmpty() && !endSet.isEmpty()) {
            // 总是选择较小的集合进行扩展，以减少下一轮处理的单词数量
            if (beginSet.size() > endSet.size()) {
                Set<String> temp = beginSet;
                beginSet = endSet;
                endSet = temp;
            }

            Set<String> temp = new HashSet<>(); // 用于存储下一轮扩展的结果，如果是队列就不需要这步
            for (String word : beginSet) {//遍历当前队列（集合）中结点，让他们走一步，每次只走一步
                char[] chs = word.toCharArray();
                // 尝试更改当前单词的每一个字符，看看是否可以接龙
                for (int i = 0; i < chs.length; i++) {
                    for (char c = 'a'; c <= 'z'; c++) {//用a到z依次替换
                        char old = chs[i]; // 保存原始字符
                        chs[i] = c;//用a-z依次替换i位置字符
                        String target = String.valueOf(chs); // 生成新单词

                        // 如果新单词在另一端集合中，说明找到了最短路径
                        if (endSet.contains(target)) return len + 1;
                        
                        // 如果新单词未访问且存在于单词列表中，则加入下一轮搜索
                        if (!visited.contains(target) && wordSet.contains(target)) {
                            temp.add(target);
                            visited.add(target); // 标记为已访问
                        }
                        chs[i] = old; // 恢复原始字符，以便下一次修改
                    }
                }
            }
            beginSet = temp; // 更新beginSet为下一轮搜索的边界
            len++; // 每完成一轮双向搜索，路径长度加1，因为我们规定，每次只走一步
        }

        return 0; // 如果无法连接开始和结束单词，返回0
    }
}