343. 整数拆分
题目
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
解题思路
- dp[i] 分拆数字i,可以得到的最大乘积为dp[i]。
- 从dp数组的含义可以默认dp[i]是最大乘积,然后可以用该定义去当做算法的一些中间值进行。
- 两种情况:拆两个数:j*(i-j) ,继续向下拆都可以表示为 j * dp [i-j]
- 这里需要知道一个前提,周长相等的四边形,面积最大的一定正方形。即拆分的每个数都尽可能相等才能让乘积最大。
- 代码中 i/2 可以这么理解:
拆分6为两个数,有这几种情况:1 * 5;2 * 4; 3 * 3; 4 *2; 5 * 1 可以看出来,拆到后面其实和前面重了。
代码
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n + 1);
dp[2] = 1;
for (int i = 3; i <= n ; i++) {
for (int j = 1; j <= i / 2; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}
return dp[n];
}
};
96. 不同的二叉搜索树
题目
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。

解题思路
- 从代码随想录的视频深刻的理解了,如果没思路,那就遍历前几个情况,把所有的都写出来找规律。(其实就是数学归纳法)
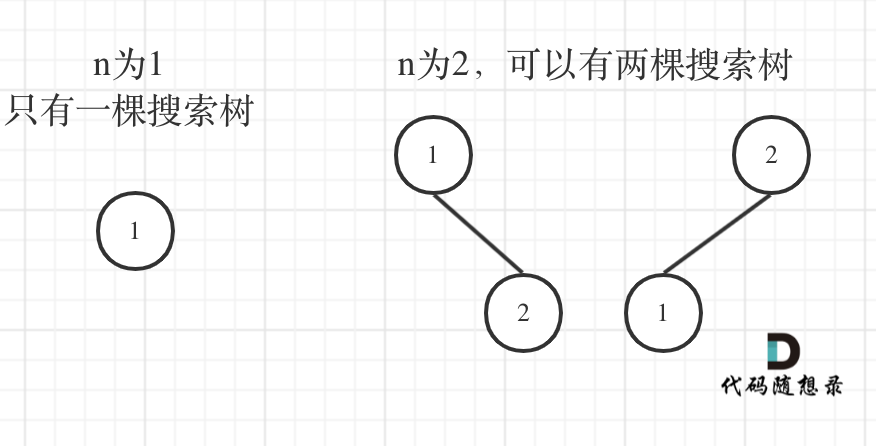

如上示例中:
当n=3, 1为根节点时,其右边有两个节点,那这两个节点可以构成的二叉搜索树个数其实就是n=2时的个数
当n=3, 2为根节点时,其左右两边各有一个节点,那这两个节点的构成情况,就是n=1时的个数
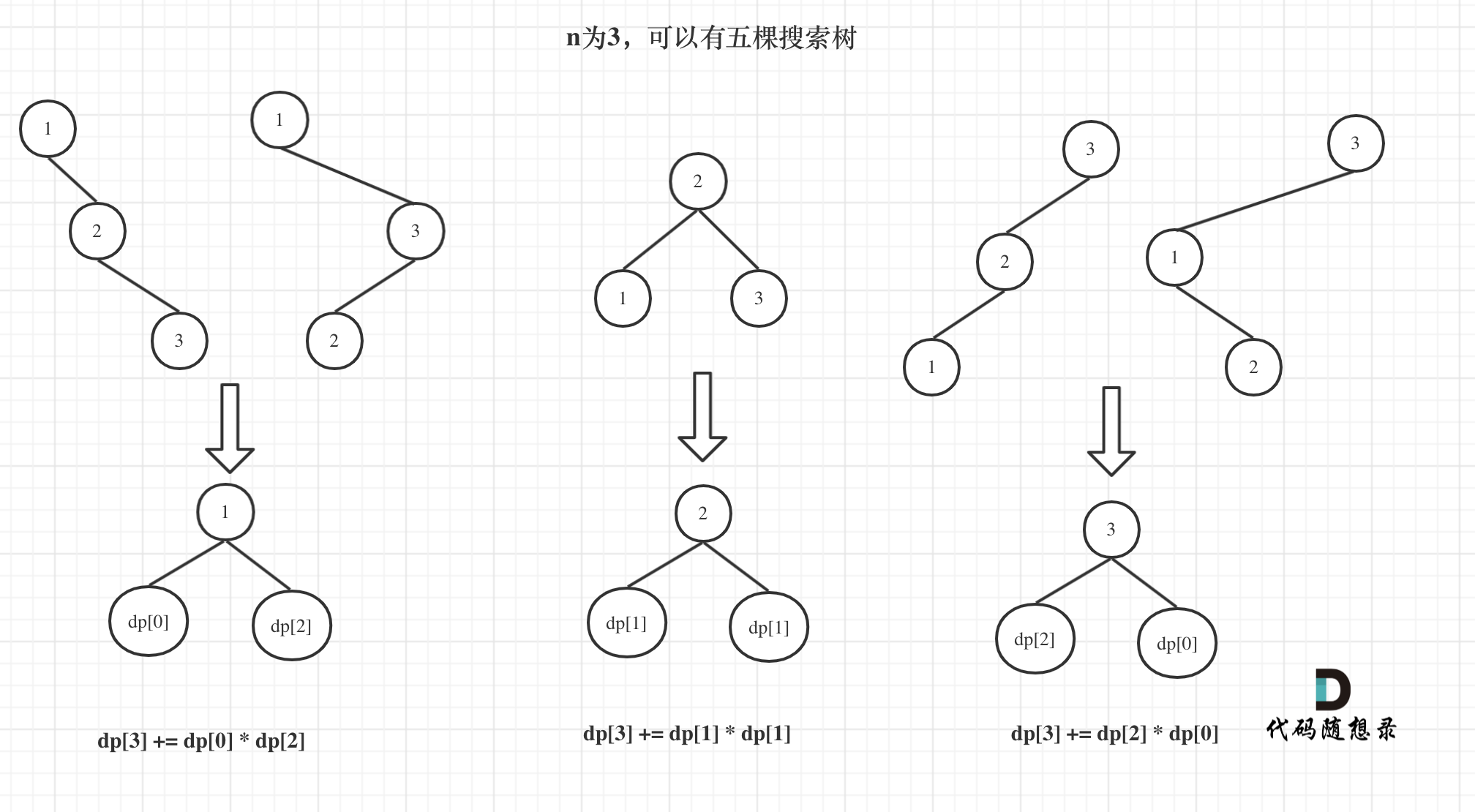
- dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。
- dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
- j相当于是头结点的元素,从1遍历到i为止。
- j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
代码
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
};