目录
前言
由来
介绍
算法原理
假设前提
一、前向传递过程(算法训练好后的使用过程)
补充:sign函数
二、训练方法(求解权重w、偏转量b)
写出损失函数
误分点选取
损失函数求导
梯度下降自确定w、b
算法实现
总结
前言
在我的第一篇《深度学习的发展历史(深度学习入门、学习指导)-CSDN博客》中,介绍了深度学习模型发展的一个全进程。在这一个深度学习历史上最早出现的就是MCP人工神经元模型,这个模型有一个相当有名的算法——感知器(也称为单层感知机)
本篇文章,我们就来讲一讲这个神经网路\深度学习邻域的老祖宗模型

由来
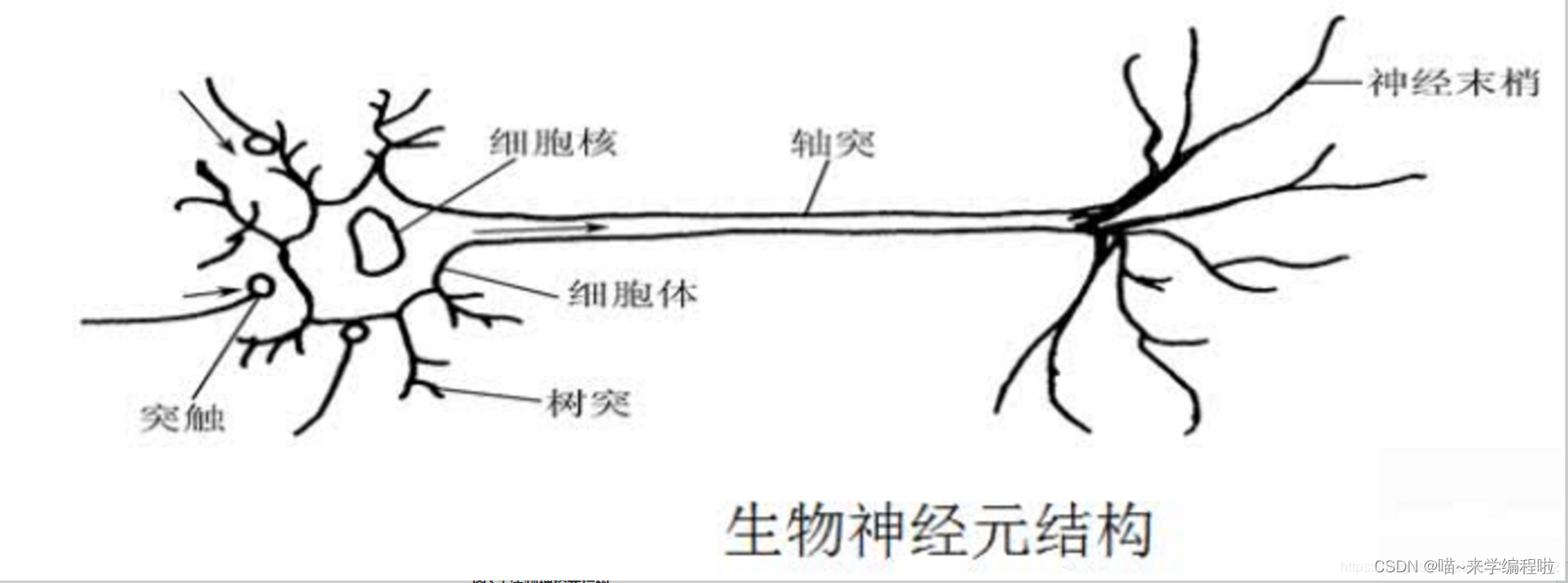
我们大脑做出每一个决定,都可以看作是接受一定输入然后在确认自身状态后,返回这个输入的输出值。举个例子:
一、
输入值:同学叫我去打篮球
输出值:拒绝同学
二、
输入值:同学叫我去打羽毛球
输出值:同意同学
这里可以看到不同的输入值,我们的输出值不一样。这就说明不同的输出值它对输出值的影响是不同的,所以对每一个输入值需要有一个权重。如何判断同意还是拒绝呢,因为输入数放到函数中输出的肯定是一个连续的值而拒绝和同意只有两个值,所以这里就需要用到激活函数(只有输出两次达到一定值后才会激活,输出1)。
介绍
单层感知机是机器学习中最基础的方法之一,其本质和逻辑回归有一定的相似,两者都是接受输入,然后会根据输入返回一个输出(两者的区别在于损失函数、激活函数选择不同)。单层感知机选用sign函数作为激活函数,选用误分类点到超平面距离的总和作为损失函数。
单层感知机只能用来解决二分类问题,对于较为复杂的分类问题无法解决。并且只能处理二分类中的线性可分问题(例如异或问题无法解决)
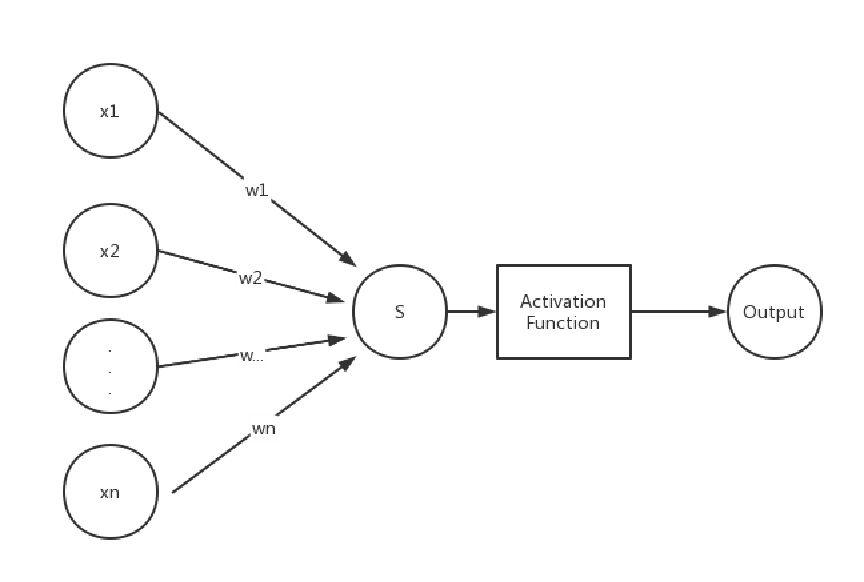
算法原理
对于一个机器学习算法,我们去研究其原理时主要从两个角度:一、前向传递过程(算法训练好后的使用过程) 二、训练过程(算法的训练过程)。对于单层感知机,我们也从这两个角度来看这个算法。
假设前提
假设有n条记录,每记录p个指标,每记录有一个输出类别,这个输出类别分为A类和B类。
一、前向传递过程(算法训练好后的使用过程)
假如已经得到训练好的单层感知机模型如下:
其中权重,以及偏转量b经过训练过程已经是已知的。
此时得到一组数据,那么代入感知机模型可以得到结果为:
由于sign函数能够将连续的结果s转变为1/-1,所以最终结果Output只有1(代表A),-1(代表B)两种情况。Output的值就是这一组数据得到的结果。
补充:sign函数
sign函数是tanh函数的极限特例:
sign(x)或者Sign(x)叫做符号函数,在数学和计算机运算中,其功能是取某个数的符号(正或负):
当x>0,sign(x)=1;
当x=0,sign(x)=0;
当x<0, sign(x)=-1
二、训练方法(求解权重w、偏转量b)
写出损失函数
一般神经网络的训练方法都是相同的,就是构造损失函数,然后对损失函数进行求导,算出损失函数极小值点下对应的权重w以及偏转量b(有时候损失函数关于w、b不是连续可导的,这种情况要另外处理)
单层感知机的损失函数就是统计所有误分类点到超平面的距离之和。
超平面:一个高维函数在高维空间上的具象化体现
这个超平面能够将高维度点分为两类:一类在超平面的一侧另一类在超平面的另一侧。
举个例子(左图为二维超平面,右图为三维超平面):
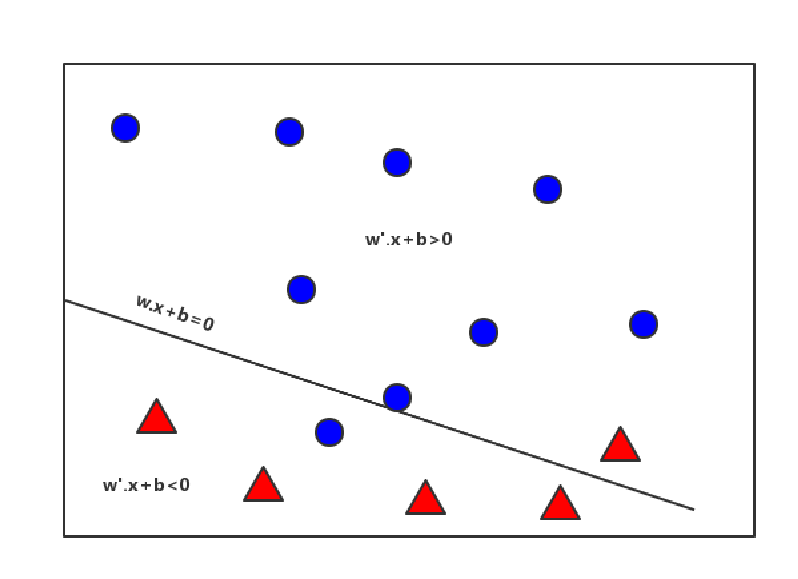
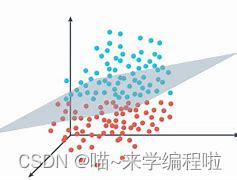
设超平面为 wx+b=0,其中w和x的维度也就是超平面所在的维度。若n个点中有m个点为误分类点,那么损失函数可以写为:
求Loss的最小值需要对Loss函数对w、b分别求偏导,但是此时Loss函数中存在绝对值以及向量长度,这都导致无法直接求导
处理方式
1、考虑到向量长度是一个常量,所以对Loss取极值时w、b的取值并没有影响,可以忽略不计
2、令超平面上方的点的类别为:A(也就是1),那此时上方点的类别值Output与
符号相同。故绝对值可以用来代替
通过上面两个处理方式最终Loss可以简化为:
误分点选取
写出损失函数后,我们不禁思考这个误分点要如何获取?显然,靠画出数据图像人为去数点是不合理的(1、wb不确定图像画不出来 2、点很多人为数点不现实)从数学的角度,Loss函数只能包含w、b两个变量,所以我们要将m转化为w、b,即找到m和wb的关系。解决这个问题,可以用计算机的思维:设计一个判断语句,若和
的符号不相同,那么这个点便是误分点,便包含在
当中。例如图中在下方的蓝色小球,其类别为1,同时
<0也成立,所以该点为误分点

损失函数求导
损失函数Loss是关于w和b的函数,对其求偏导时,由于w是一个向量,Loss本身也是一个向量,所以需要用到矩阵求导的知识。这里设计的是矩阵求导中的向量关于向量求导,这里附上求导的结果公式(想要了解原理的友友们可以自己去详细看看矩阵求导的内容)(下图为生信小兔手写)
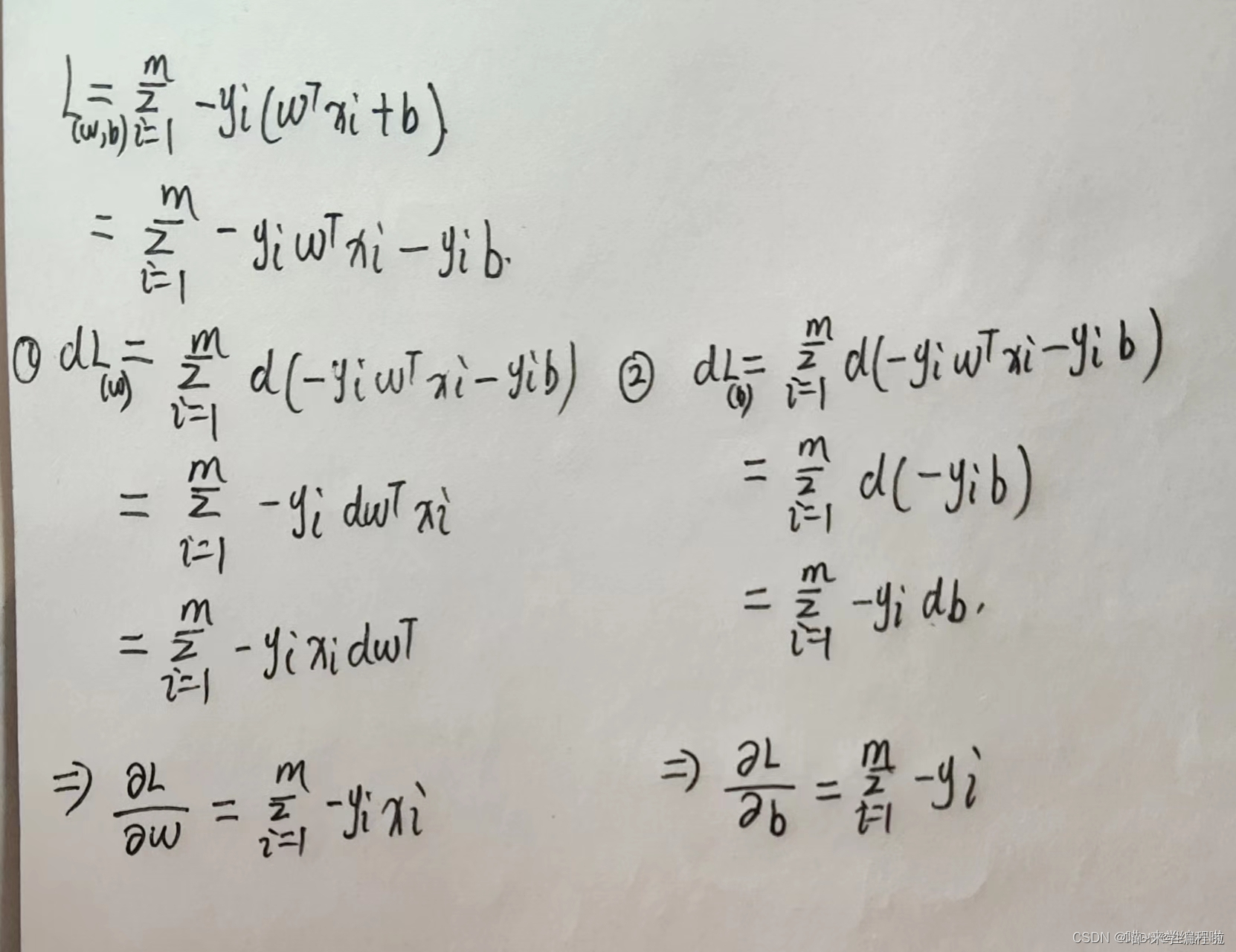
图中的w为向量需要用到矩阵求导公式,而b仅仅就是一个变量直接求导即可(图中每个地方都可以去掉一个符号,因为前文对AB对应的数做了调整)
最终求导后的结果为:
梯度下降自确定w、b
由于此时令两个求导结果的值等于0,是不存在唯一的共同解的。这个时候我们只能选择极大似然估计或者梯度下降的方式去求导离极值最近的一个值。
梯度下降
流程:
一、随机生成一个w,b(即待下降的参数)
二、求出此时随机生成的w,b关于Loss的导数
三、利用上面求得的dw、db的关系式,不停循环得到最终的dw、db值
四、令
生成新的w(alpha为学习率,n为样本数目)
五、令
生成新的b
六、利用新的w、b生成新的分割线,参与下一轮的训练,重复三四五步骤
定义:
、
称为梯度
特别点:
1、在利用梯度进行下降的时候,除n是为了对梯度归一化处理,使得梯度更加平稳,不会受样本数目的影响
2、学习率是梯度下降算法中一个重要的超参数,它控制着参数在每次更新时的步长
随机梯度下降(SGD)
定义:
SGD算法是从样本中随机抽出一组,训练后按梯度更新一次,然后再抽取一组,再更新一次。简单来说就是,将一个大数据分为多组小数据,用每一小组进行训练得到训练结果,并将结果用于下一次训练
分类:
1.SGD是最基本的随机梯度下降,它是指每次参数更新只使用一个样本,这样可能导致更新较慢;
2.Batch-SGD是批随机梯度下降,它是指每次参数更新使用所有样本,即把所有样本都代入计算一遍,然后取它们的参数更新均值,来对参数进行一次性更新,这种更新方式较为粗糙;
3.Mini-Batch-SGD是小批量随机梯度下降,它是指每次参数更新使用一小批样本这三类得区别仅仅在于每次随机抽取得组的大小,三类的抽取都是随机的
本题选用Batch-SGD
优点:
一、小组训练便返回结果使得在数据量很大时,不必要全部训练完便可以得到一个较好得结果
二、随机抽取使得数据之间的相关性降低,让准确度更好
三、每次抽取一组数据计算出新计算的dw、db后便更新w、b,产生新的分割线。利用这个分割线再去判断误分点
四、Batch-SGD和一般的SGD的区别在于,更新权重和梯度是取每一个batch的平均值进行的。相较于SGD不用每次都更新权重和梯度效率将提升,但是每一个批次取平均值更新一次使得更新的权重和梯度较为粗糙。
Batch—SGD流程:
一、设定一个BatchLength,表示每一训练组的大小
二、利用zip函数与list函数将x、y打包成元组放在data数组中(元素为xy元组)
三、利用batches数组,将data数组切片处理(data[i:i+BatchLength]为一组)
四、在每一个batches数组元素上进行组内训练(重复上面梯度下降的过程)
算法实现
在这里以dry_bean_dataset数据集为例。为了直观体现该模型的效果,我们仅选取MajorAxisLength和MinorAxisLength两个指标,数据选取前3500组数据,此时数据集仅含有SEKER和BARBUNYA两类。
在数据较少(如几十组数据)时,可以使用所有数据进行训练;对于数据较多的情况(几千甚至几万以上),用所有数据进行训练速度会很慢,效果也很差,所以可以采用随机梯度下降法,每次从中选取部分数据进行训练。代码如下:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
class perceptron:
def __init__(self,x,y,alpha=0.01,circle=500,batchlength=20): #python中函数都有一个self参数,表示实例本身(这里是一个具体的向量机)
#init中定义的self.变量就是这个类所有的属性
self.x=x #训练样本数据中的各指标数
self.y=y #训练样本数据中各组数据对应的类别
self.alpha=alpha #学习率
self.circle=circle #学习轮数
self.n=x.shape[0] #样本的数量
self.p=x.shape[1] #样本的指标个数
self.w=np.random.normal(size=(self.p,1)) #利用np随机生成(normal法)向量w,其规模就是(指标个数,1)
self.b=np.random.normal(size=1) #利用np随机生成(normal法)常量b
self.batchlength=batchlength #每次训练样本中使用的数据个数,随机梯度下降法
def batches(self): #batches作用就是让梯度下降分组进行,而不是
data=list(zip(self.x,self.y)) #zip作用为压缩两个元组一一合并返回值是一个zip压缩包不能直接浏览内容,list将合并后的元组以列表形式呈现方便浏览
np.random.shuffle(data) #将data内容打乱
batches=[data[i:i+self.batchlength] for i in range(0,self.n,self.batchlength)]
return batches
def sign(self,x): #激活函数sign
if x>0:
return 1
elif x<0:
return -1
else:
return 0
def train(self):
for i in range(self.circle): #省略了(0,self.circle)
print('the {} circle'.format(i)) #{}作用是在字符串中插入数字
for batch in self.batches(): #每一个batch都可以认为是一组数组,数组中每个元素都是一个元组,batches()返回值是数组的数组
dw=0
db=0 #用来实现数学表达式中的求和的中间值
num=1; #误分类点的个数
for x,y in batch:
if y*(np.dot(self.w.T,x.T)+self.b)>=0: #同号表示不是误分点
continue
else:
dw += -y * x.T
db += -y
num += 1
if num!=0:
self.w -= self.alpha * dw / num
self.b -= self.alpha * db / num
else:
continue
#每一轮对所有数据进行学习后,都画出新的分割线和分割点
color=[]
for c in self.y:
if c==1:
color.append('green')
else:
color.append('red')
x = np.arange(180, 470, 1) #根据数据的范围确定画图中x的范围
y = -self.w[0] * x / self.w[1] - self.b / self.w[1] # 分割线
plt.plot(x, y)
plt.scatter(np.array(self.x[:, 0]), np.array(self.x[:, 1]), color=color)
plt.xlim([180, 470])
plt.ylim([160, 320])
plt.pause(1)
plt.clf()
# x = np.arange(180, 470, 1) # 根据数据的范围确定画图中x的范围
# y = -self.w[0] * x / self.w[1] - self.b / self.w[1] # 分割线
# plt.plot(x, y)
# plt.scatter(np.array(self.x[:, 0]), np.array(self.x[:, 1]), color=color)
# plt.xlim([180, 470])
# plt.ylim([160, 320])
# plt.pause(1)
# plt.clf()
def prediction(self,x):
s=np.dot(self.w.T,x)+self.b
output=self.sign(s)
return output
if __name__=='__main__': #下面语句作为主程序单独运行时执行,作为模块导入时不执行
df=pd.read_excel('Dry_Bean_Dataset.xlsx') #读取excel文件
df.to_csv('Dry_Bean_Dataset.csv',index=False) #将excel文件另存为csv文件
df=pd.DataFrame(pd.read_csv('Dry_Bean_Dataset.csv')) #将csv文件转变为dataframe对象,然后就可以用dataframe对象下的许多函数来进行数据分析处理
x=df.loc[0:3500, 'MajorAxisLength':'MinorAxisLength'] #对列表进行切片操作,对矩阵本身的操作(筛选、删除等)用[]进行
y=df.loc[0:3500, 'Class']
X=np.mat(x) #将列表对象转为numpy矩阵
Y=[]
color=[]
#对数据进行可视化画图
for c in y:
if c=='SEKER':
Y.append(1)
else:
Y.append(-1)
p = perceptron(x=X, y=Y)
p.train()代码中直接将数据集xlsx文件与程序放在一个文件夹内,同时有将xlsx文件转化为csv文件的操作。
关键点:
图中的超平面为,要将这个超平面画出来,考虑到这个超平面在本数据集中是二维的,所以画这个超平面也就是画一条直线。因为w=(wo,w1)x=(x1,x2),所以可以另其中一个x2为y,x1为x去画这个直线,因此直线的方程就是:
。
因此代码中有: y = -self.w[0] * x / self.w[1] - self.b / self.w[1] # 分割线这一句子
最终结果图为:
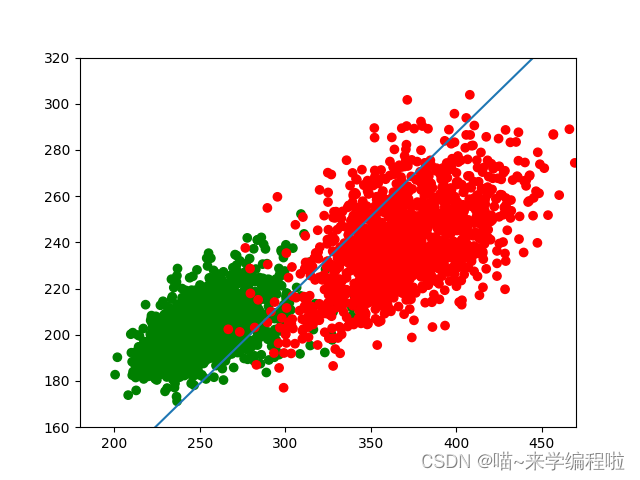
我们肉眼可以看出,这个分割方式不会是最好的分割方式,这说明机器对于单层感知器来说其准确率并不是很高的
总结
单层感知机虽然整体思路非常简单,但是其确实更加复杂的神经网络学习的基础。通过单层感知机的学习我们可以学到损失函数、梯度下降、矩阵求导、数据分析处理等在所有机器学习中都可以使用的知识。同时单层感知器存在无法处理异或问题、准确度低等缺陷,但是其组合在一起变成多层感知机便可以处理这些问题。
(由于本人也是刚刚接触机器学习算法,本篇内容参考并沿用了大量其他大佬们的资料,在这里向“生信小兔”表示感谢,通过他的文章真的学了挺多)
还是想厚脸皮的求赞啦~~~人工智能领域小白