- 常见的期权定价模型有BSM模型、二叉树模型以及蒙特卡洛定价模型。
BS模型
- 在一系列的假设条件下,该模型将期权的价值表示成为标的资产价格、行权价格、无风险利率、期权剩余期限和标的资产波动率的函数。即一旦定量的给出上述5个影响因子的数值,就可以通过BSM模型计算得到相应的期权的价值。
- 该数学模型的优点就是形式简洁,计算快速。但是其缺点也比较明显,比如它只能用于欧式期权定价,对美式期权及奇异期权显得力不从心。
二叉树模型
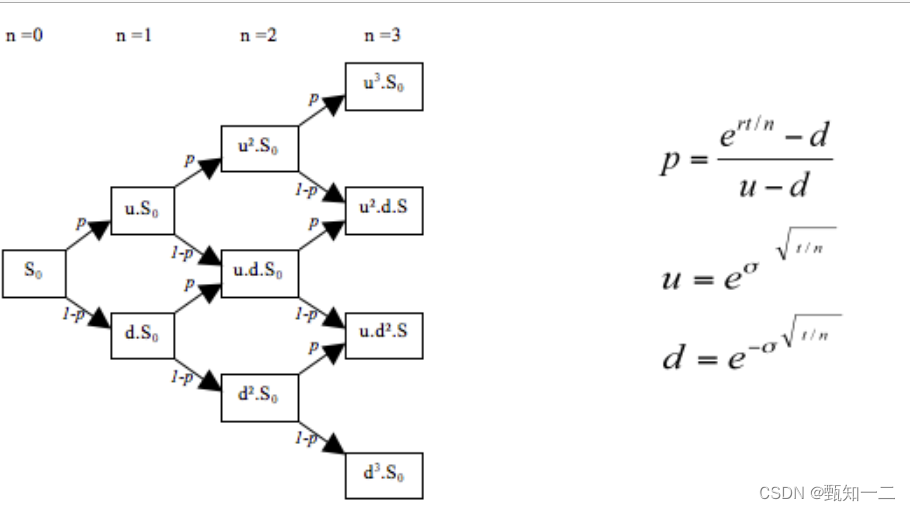
- 其主要设计思想是假设标的资产在下一个时刻只有两种运行可能,即以固定的概率上升或下降。
- 由此给出标的资产价格变动的路径,并基于此路径计算出期权的价值。该方法是为复杂期权,如美式期权和奇异期权定价的基本手段。
- 二叉树方法简单直观,但其计算精度取决于计算的步数,计算效率较低。
- 当二叉树模型相继两步之间的时间长度趋于零的时候,模型等价于BSM模型

- 使用二叉树进行期权定价,需要从已知条件中算出股票价格上涨到的比率,股票价格下跌到的比率,股票价格上涨的概率等指标,从左到右生成二叉树,最后根据生成的二叉树,从右向左计算期权价值。

蒙特卡洛模拟
- 蒙特卡洛模拟方法的实质是利用随机数发生器模拟出许多不同的价格路径,并基于这些路径,得出期权的期望收益,进而对其贴现得出期权价值。
- 该模型也对金融工程领域的发展起到重要作用,其优点是能处理更加复杂的对标的资产价格运动路径的假设,并且能够方便的处理非单一标的资产期权的定价问题。
- 但其结果的精度取决于模拟运算次数,精度越高,计算速度越慢。
第一步,划定时间范围、步长、总模拟路径次数
第二步,模拟股价的变化路径。
第三步,检验预测精度
第四步,基于模拟的股价数据路径,构造期权价格数据路径