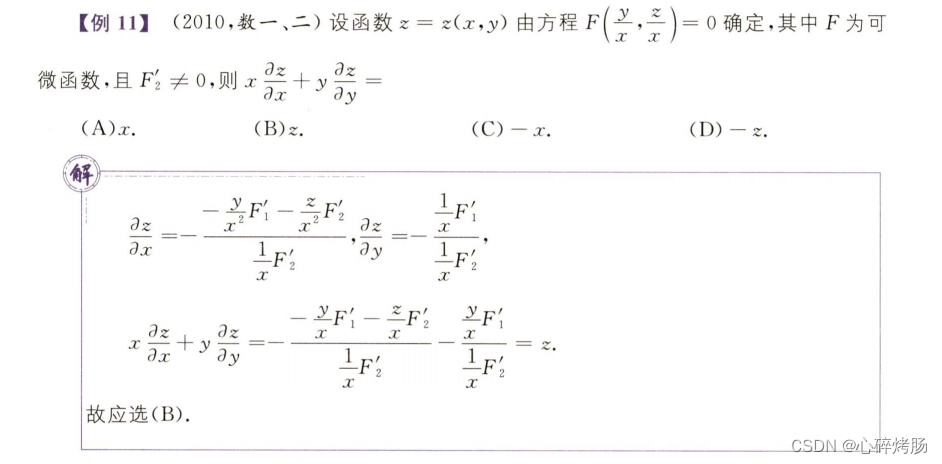
多元函数微分法:
一、复合函数微分法
二、隐函数微分法
三、复合函数偏导数与全微分
四、隐函数偏导数与全微分
目录
一、复合函数微分法
二、隐函数微分法
三、复合函数偏导数与全微分
四、隐函数偏导数与全微分
一、复合函数微分法

二、隐函数微分法


补充:
隐函数求导的常用方法:(下面的字母z我写成了大写,并没有任何实际含义,只是因为小z显示不清楚,所有我换成了大Z,能让大家看的更清楚)
1.公式法 ,
2.方程两边同时对x求偏导(y是常数,z是关于x的函数)可得
3.,利用微分形式不变性,两边同时求微分得
;
整理后可得
三、复合函数偏导数与全微分



复合函数求偏导一般方法:
方法一:
1.换元,
2.带入复合函数偏导公式即可
方法二:
补充解释 f1跟f2的含义:
求抽象复合函数的偏导数时,由于是复合,所以先对外层求导,再对内求导。这一点没啥问题;由于函数是,对应法则存在但未知,就用脚标1,2…代替对应法则。自然求一阶导时记为f',二阶导为f'';对第一个自变量求导脚标就带上1,对第二个自变量求导脚标就带上2;(复合函数的两个自变量分别为u,v)

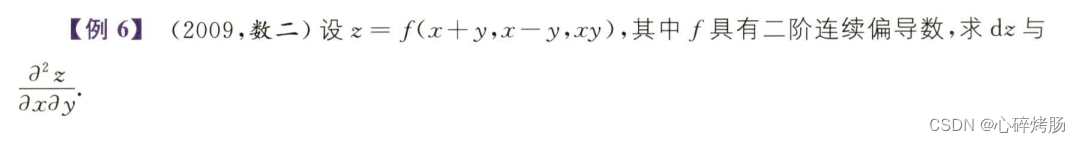

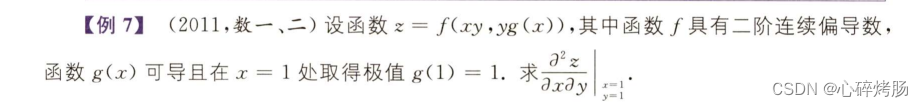



四、隐函数偏导数与全微分