分解质因数的朴素算法
最简单的算法即为从 [2, sqrt(N)] 进行遍历。
vector<int> breakdown(int N) {
vector<int> result;
for (int i = 2; i * i <= N; i++) {
if (N % i == 0) { // 如果 i 能够整除 N,说明 i 为 N 的一个质因子。
while (N % i == 0) N /= i;
result.push_back(i);
}
}
if (N != 1) { // 说明再经过操作之后 N 留下了一个素数
result.push_back(N);
}
return result;
}
这个算法当 n 是质数时拥有最差时间复杂度 O(n) ,不过可以先用米勒-拉宾特判一下 n 是不是质数,这样的话最差时间复杂度就是当 n 是质数的平方时的 O(sqrt (n)) 了
Pollard_rho将一个数分解为质因数相乘的形式
如:200 = 22255
Pollard_rho算法是找到一个数的最大质因数,我参考此算法进行修改,实现了将一个数分解为质因数相乘形式的程序。
#include <iostream>
#include <stdlib.h>
#include <vector>
int t;
long long max_factor, n;
std::vector<long long> factor; // 存储质因数
long long gcd(long long a, long long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
long long quick_pow(long long x, long long p, long long mod) { // 快速幂
long long ans = 1;
while (p) {
if (p & 1) ans = (__int128)ans * x % mod;
x = (__int128)x * x % mod;
p >>= 1;
}
return ans;
}
bool Miller_Rabin(long long p) { // 判断素数
if (p < 2) return 0;
if (p == 2) return 1;
if (p == 3) return 1;
long long d = p - 1, r = 0;
while (!(d & 1)) ++r, d >>= 1; // 将d处理为奇数
std::vector<long long> ud = {2, 325, 9375, 28178, 450775, 9780504, 1795265022};
for (long long a:ud) {
long long x = quick_pow(a, d, p);
if (x == 1 || x == p - 1) continue;
for (int i = 0; i < r - 1; ++i) {
x = (__int128)x * x % p;
if (x == p - 1) break;
}
if (x != p - 1) return 0;
}
return 1;
}
long long Pollard_Rho(long long x) {
long long s = 0, t = 0;
long long c = (long long)rand() % (x - 1) + 1;
int step = 0, goal = 1;
long long val = 1;
for (goal = 1;; goal *= 2, s = t, val = 1) { // 倍增优化
for (step = 1; step <= goal; ++step) {
t = ((__int128)t * t + c) % x;
val = (__int128)val * abs(t - s) % x;
if ((step % 127) == 0) {
long long d = gcd(val, x);
if (d > 1) return d;
}
}
long long d = gcd(val, x);
if (d > 1) return d;
}
}
void fac(long long x) {
if (x <= max_factor || x < 2) return;
if (Miller_Rabin(x)) { // 如果x为质数
max_factor = std::max(max_factor, x); // 更新答案
return;
}
long long p = x;
while (p >= x) p = Pollard_Rho(x); // 使用该算法
while ((x % p) == 0) x /= p;
fac(x), fac(p); // 继续向下分解x和p
}
void decompose(long long n) { // 将n分解为质因数相乘的形式
srand((unsigned)time(NULL));
max_factor = 0;
fac(n);
if(max_factor == n) { // 最大的质因数是自己
factor.push_back(max_factor);
}
else {
factor.push_back(max_factor);
n /= max_factor;
decompose(n);
}
}
int main() {
std::cout << "----start decompose n: [exit please input number 0 !]----" << std::endl;
while(1) {
std::cout << "input number: ";
std::cin >> n;
if(n == 0) {
std::cout << "stop and exit program!" << std::endl;
break;
}
decompose(n);
std::cout << n << " = ";
for(std::vector<long long>::iterator it = factor.begin(); it != factor.end()-1; ++it) {
std::cout << *it << "*";
}
std::cout << *(factor.end()-1) << std::endl;
std::vector<long long>().swap(factor);
}
return 0;
}
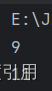
程序功能展示
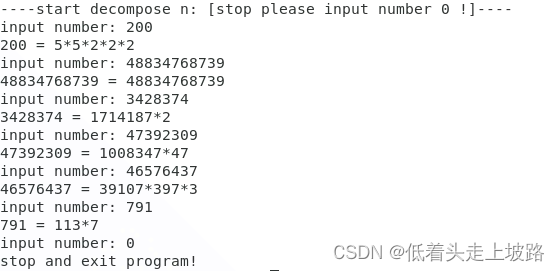
参考文章
[1] https://oi-wiki.org/math/number-theory/pollard-rho/
[2] https://zhuanlan.zhihu.com/p/267884783
[3] Miller Rabin素数判定






![[Java基础揉碎]枚举](https://img-blog.csdnimg.cn/direct/34318677e47646f18df6ea962264fd06.png)
