递归与递推
递归
1.指数型枚举
解析:从 1 ∼ n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
思路:枚举每一位对应的数字选与不选,例如:第一位对应的数字为1,有一种方案是选1,另外一种方案是不选

AcWing 92. 递归实现指数型枚举
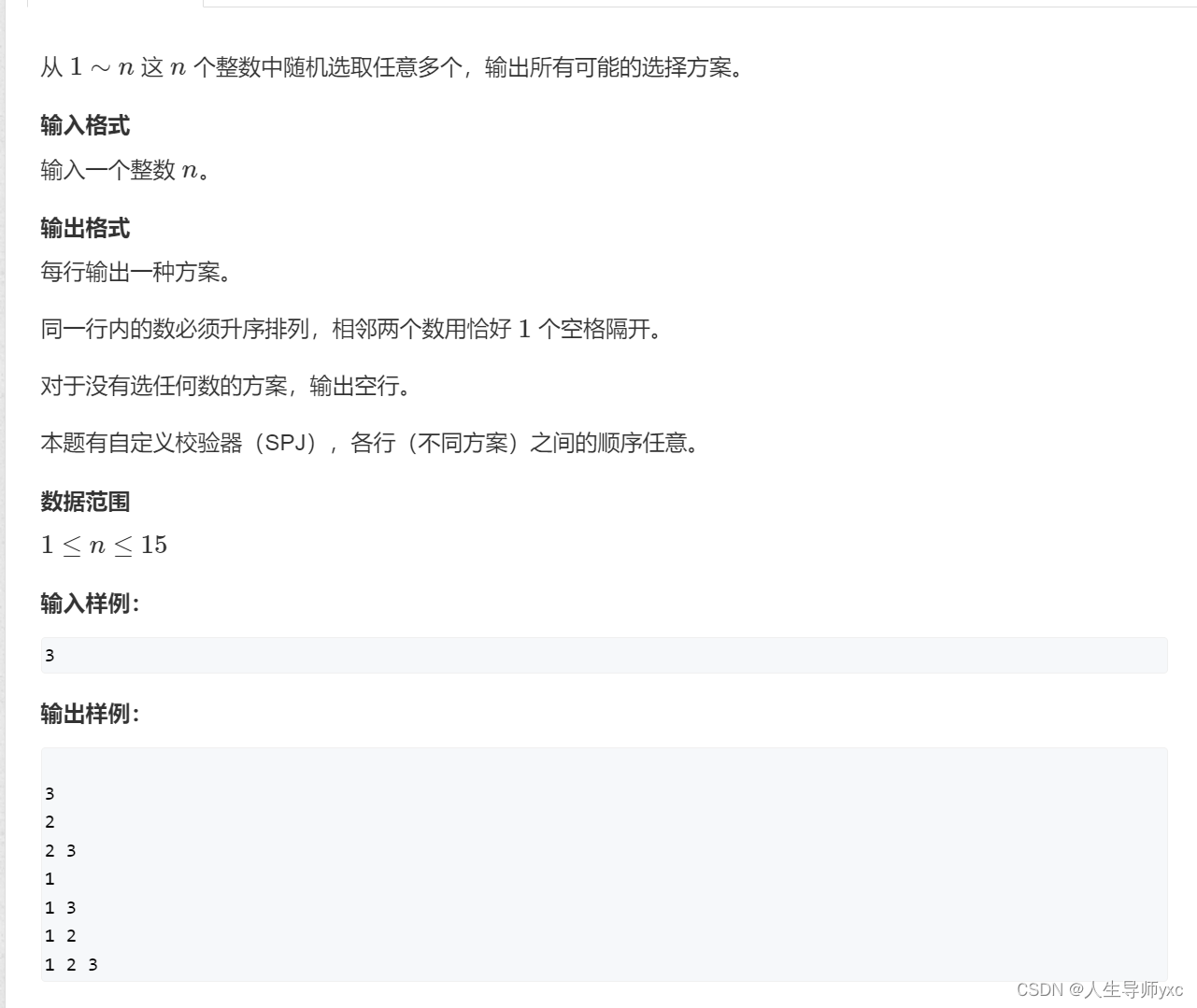
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;
int n;
bool st[N];
void dfs(int u)
{
if (u > n)
{
for (int i = 1; i <= n; i ++)
{
if (st[i]) cout << i << ' ';
}
cout << endl;
return ; //选完三个数,回溯
}
//选当前位置所对应的数
st[u] = true; //选的数标记为true
dfs(u + 1); //递归到下一位
//不选当前位置所对应的数
st[u] = false;
dfs(u + 1);
}
int main()
{
cin >> n;
dfs(1);
return 0;
}2.排列形枚举
解析:把 1 ∼ n 这 n 个整数排成一行后随机打乱顺序
思路:考虑每一位可以填哪几个数,用过的数字需要标记

AcWing 94. 递归实现排列型枚举

#include <algorithm>
#include <iostream>
using namespace std;
const int N = 20;
int n;
int path[N], cnt;
bool st[N];
void dfs(int u)
{
if (u > n)
{
for (int i = 1; i <= n; i ++)
cout << path[i] << ' ';
cout << endl;
return; //回溯
}
for (int i = 1; i <= n; i ++)
{
if (!st[i])
{
path[u] = i;
st[i] = true; //标记
dfs(u + 1);
st[i] = false; //恢复现场
}
}
}
int main()
{
cin >> n;
dfs(1);
return 0;
}3.组合型枚举
解析:从 1∼n 这 n个整数中随机选出 m个,输出所有可能的选择方案。
思路:画一棵递归搜索树

AcWing 93. 递归实现组合型枚举

输入样例:
5 3
输出样例:
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5 #include <iostream>
using namespace std;
const int N = 50;
int path[N];
bool st[N];
int n, m;
void dfs(int u, int last)
{
//剪枝:当可填入数字小于当前空缺的位数时
if (n - last < m - u) return;
//当所有位数全部填满,输出结果,回溯
if (u > m)
{
for (int i = 1; i <= m; i ++) printf("%d ", path[i]);
puts("");
return;
}
//填入数字
for (int i = last; i <= n; i ++)
{
if (!st[i])
{
path[u] = i;
st[i] = true;
dfs(u + 1, i);
st[i] = false; //恢复现场
}
}
}
int main()
{
scanf("%d%d", &n, &m);
dfs(1, 1);
return 0;
} 
递推
斐波那契
解析:其数值为:1、1、2、3、5、8、13、21、34……在数学上,这一数列以如下递推的方法定z义:F(0)=1,F(1)=1, F(n)=F(n - 1)+F(n - 2)
AcWing 717. 简单斐波那契
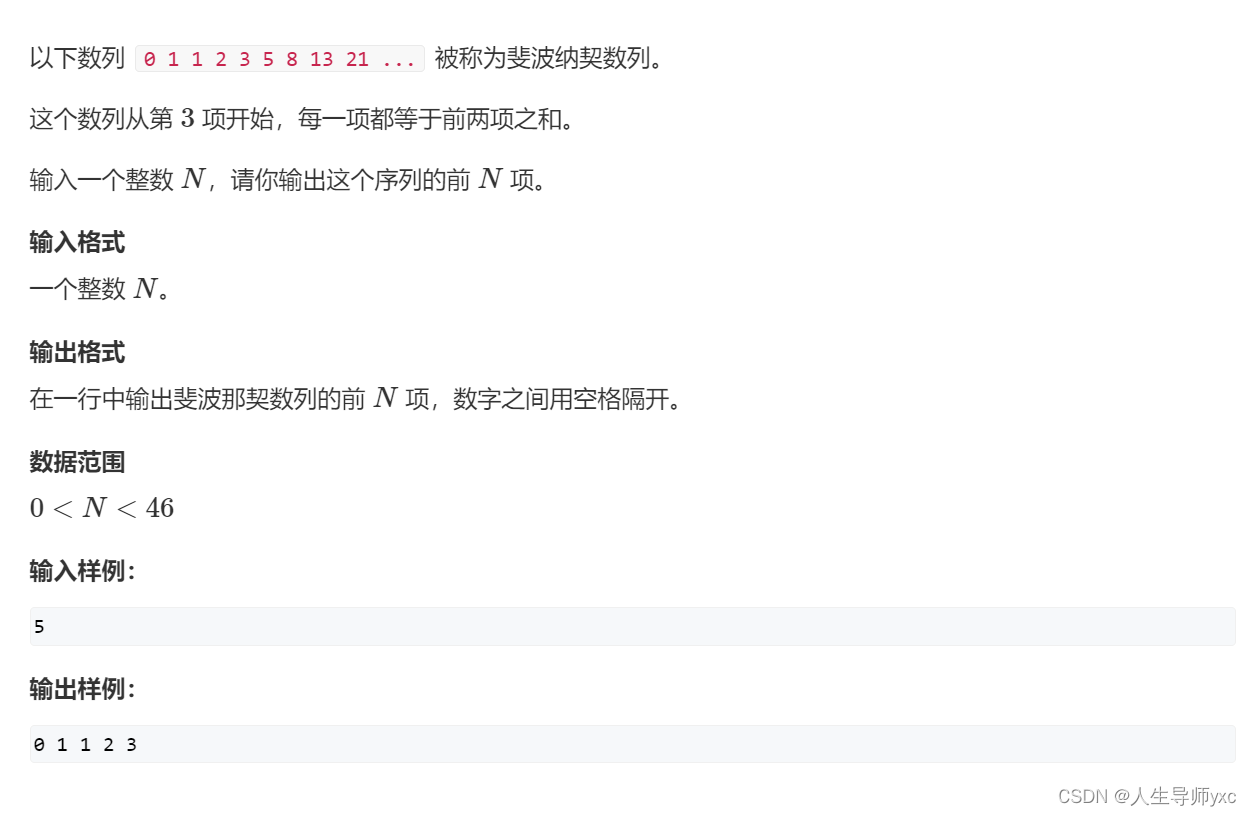
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 50;
int n, a[N];
int main()
{
cin >> n;
if (n == 1) cout << "0" << endl;
else
{
a[0] = 0;
a[1] = 1;
cout << a[0] << ' ' << a[1];
for (int i = 2; i < n; i ++)
{
a[i] = a[i - 1] + a[i - 2];
cout << ' ' << a[i];
}
cout << endl;
}
return 0;
}习题:
费解的开关
解析:每一盏灯都有两种选择 : 按或者不按。
通过递推发现规律:1. 当第一行的操作方案确定时,剩余行的操作方案也确定了
2.前一行的状态影响下一行的操作
举例:
假设第一行选择某一种方案进行操作后的状态如图所示:

第一行的状态决定了第二行的操作(要使得第一行灯灭的格子变亮,就必须对该格子下方的方格进行操作):
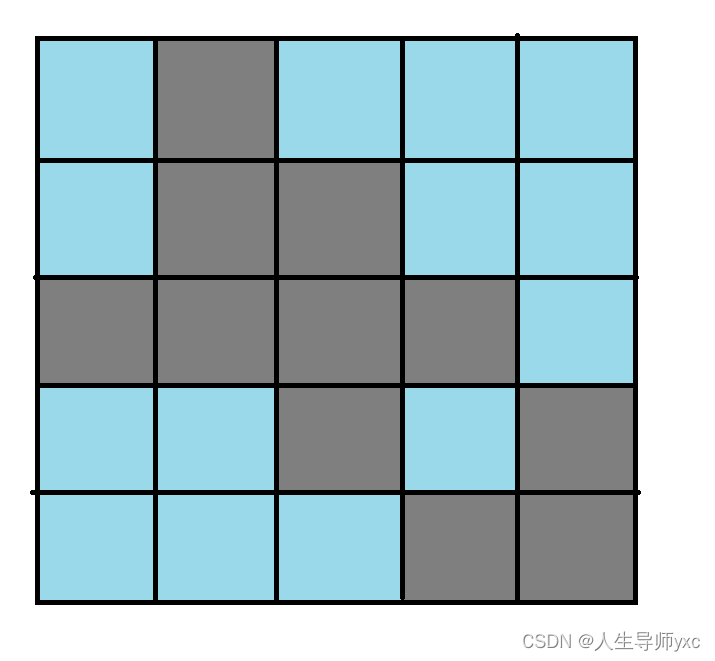

操作完成后第一行的格子全亮
以此类推......
思路:
1.枚举第一行格子的每一种操作方案
2.枚举前四行的状态,操作下一行,使得前四行的格子全亮
3.判断最后一行格子是否全亮
题目:
你玩过“拉灯”游戏吗?
25盏灯排成一个 5×5 的方形。
每一个灯都有一个开关,游戏者可以改变它的状态。
每一步,游戏者可以改变某一个灯的状态。
游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字 1 表示一盏开着的灯,用数字 0 表示关着的灯。
给定一些游戏的初始状态,编写程序判断游戏者是否可能在 6 步以内使所有的灯都变亮。
输入格式
第一行输入正整数 n,代表数据中共有 n 个待解决的游戏初始状态。
以下若干行数据分为 n组,每组数据有 5 行,每行 5 个字符。
每组数据描述了一个游戏的初始状态。
各组数据间用一个空行分隔。
输出格式
一共输出 n 行数据,每行有一个小于等于 6 的整数,它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态,若 6 步以内无法使所有灯变亮,则输出 −1。
数据范围
0<n≤500
输入样例:
3 00111 01011 10001 11010 11100 11101 11101 11110 11111 11111 01111 11111 11111 11111 11111输出样例:
3 2 -1
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10;
int n;
int g[N][N], backup[N][N];
string s[N];
int dx[] = {0, 1, -1, 0 , 0};
int dy[] = {0, 0, 0, 1, -1};
void turn(int x, int y)
{
for (int i = 0; i < 5; i ++)
{
int a = x + dx[i], b = y + dy[i];
if (a >= 0 && a < 5 && b >= 0 && b < 5)
{
if (g[a][b] == 0) g[a][b] = 1;
else g[a][b] = 0;
}
}
}
int main()
{
scanf ("%d", &n);
while (n --)
{
int res = 10;
for (int i = 0; i < 5; i ++) cin >> s[i];
for (int i = 0; i < 5; i ++)
for (int j = 0; j < 5; j ++)
g[i][j] = s[i][j] - '0';
for (int op = 0; op < 32; op ++)
{
memcpy(backup, g, sizeof g);
int step = 0;
for (int i = 0; i < 5; i ++)
{
if (op >> i & 1)
{
step ++;
turn(0, i);
}
}
for (int i = 0; i < 4; i ++)
{
for (int j = 0; j < 5; j ++)
{
if (g[i][j] == 0)
{
step ++;
turn(i + 1, j);
}
}
}
bool dark = false;
for (int i = 0; i < 5; i ++)
{
if (g[4][i] == 0)
{
dark = true;
break;
}
}
if (!dark) res = min(res, step);
memcpy(g, backup, sizeof backup);
}
if (res > 6) res = -1;
cout << res << endl;
}
}AcWing 1209. 带分数

解析: n = a + b / c
经过变形得:b = nc - ac
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 10;
bool st[N], backup[N];
int n, ans;
//n = a + b / c
//b = nc - ac
//判断a, b, c是否满足要求
bool check(int a, int c)
{
long long b = n * (long long)c - a * c;
if (!a || !b || !c) return false;
memcpy(backup, st, sizeof st);
while (b)
{
int x = b % 10;
b /= 10;
if (!x || backup[x]) return false;
backup[x] = true;
}
for (int i = 1; i <= 9; i ++)
if (!backup[i]) return false;
return true;
}
void dfs_c(int u, int a, int c)
{
if (u > 9) return;
if (check(a, c)) ans ++;
for (int i = 1; i <= 9; i ++)
{
if (!st[i])
{
st[i] = true;
dfs_c(u + 1, a, c * 10 + i);
st[i] = false;
}
}
}
//u当前用了几位数 当前a为多少
void dfs_a(int u, int a)
{
if (a >= n) return;
if (a) dfs_c(u, a, 0);
for (int i = 1; i <= 9; i ++)
{
if (!st[i])
{
st[i] = true;
dfs_a(u + 1, a * 10 + i);
st[i] = false;
}
}
}
int main()
{
scanf("%d", &n);
dfs_a(0, 0); //dfs_a(u, a);
printf("%d\n", ans);
return 0;
}AcWing 116. 飞行员兄弟

输入样例:
-+--
----
----
-+--
输出样例:
6
1 1
1 3
1 4
4 1
4 3
4 4分析:
类似于费解的开关:初始状态为4 * 4, 对于这16个可操作的位置,每一个位置可选方案为两种,一共有2^16种操作方案,枚举这2^16种方案
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 10;
char g[N][N], backup[N][N];
vector<PII> ans;
void turn(int x, int y)
{
for (int i = 0; i < 4; i ++)
{
if (g[x][i] == '+') g[x][i] = '-';
else g[x][i] = '+';
if (g[i][y] == '+') g[i][y] = '-';
else g[i][y] = '+';
}
if (g[x][y] == '+') g[x][y] = '-';
else if (g[x][y] == '-') g[x][y] = '+';
}
int main()
{
for (int i = 0; i < 4; i ++) scanf("%s", g[i]);
for (int op = 0; op < (1 << 16); op ++)
{
memcpy(backup, g, sizeof g);
vector<PII> tmp;
int step = 0;
for (int i = 0; i < 4; i ++)
{
for (int j = 0; j < 4; j ++)
{
int x = i * 4 + j;
if (op >> x & 1)
{
turn(i, j);
tmp.push_back({i + 1, j + 1});
step ++;
}
}
}
bool flag = true;
for (int i = 0; i < 4; i ++)
{
for (int j = 0; j < 4; j ++)
{
if (g[i][j] == '+')
{
flag = false;
}
}
}
if (flag)
{
if (ans.empty() || tmp.size() < ans.size())
{
ans = tmp;
}
}
memcpy(g, backup, sizeof g);
}
cout << ans.size() << endl;
for (auto it : ans) cout << it.first << ' ' << it.second << endl;
}二分与前缀和
二分查找
图解分析:
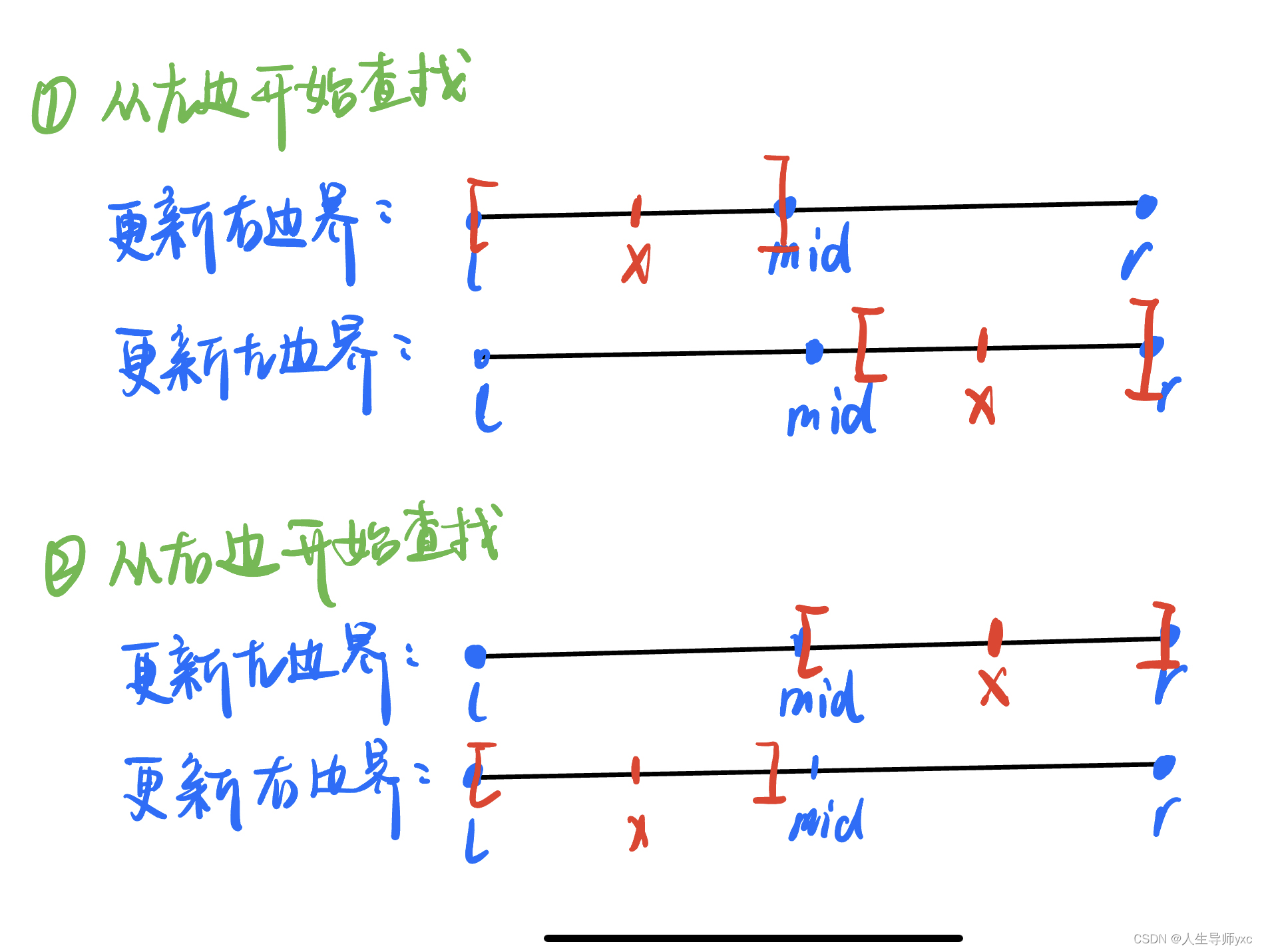
模板:
从左边开始找:
int l = 0;
int r = n - 1;
while (l < r)
{
int mid = (l + r) / 2;
if (a[mid] >= x) r = mid;
else l = mid + 1;
}从右边开始找:
l = 0;
r = n - 1;
while(l < r)
{
int mid = (l + r + 1) / 2;
if (a[mid] <= x) l = mid;
else r = mid - 1;
}大概思路:
根据a[mid]与x的大小关系,不断更新左右区间
二分例题:
AcWing 1221. 四平方和

思路:
1.先枚举c和d,将c和d的结果用一个结构体存储起来
2.再枚举a和b,在存储的结构体数组中查找与a和b互补的结果
注意:结构体数组要按字典序排列,必须从小到大依次排好,只有这样,查找到的第一个结果是按字典序排列的
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 25000010;
int cnt;
struct Sum {
int s, c, d;
bool operator < (const Sum &t)const{
if (s != t.s) return s < t.s;
if (c != t.c) return c < t.c;
return d < t.d;
}
}sum[N];
int main()
{
int n;
scanf("%d", &n);
for (int c = 0; c * c <= n; c ++)
{
for (int d = c; c * c + d * d <= n; d ++)
{
sum[cnt ++] = {c * c + d * d, c, d};
}
}
sort(sum, sum + cnt);
for (int a = 0; a * a <= n; a ++)
{
for (int b = a; a * a + b * b <= n; b ++)
{
int t = n - (a * a + b * b);
int l = 0, r = cnt - 1;
while (l < r)
{
int mid = (l + r) / 2;
if (sum[mid].s >= t) r = mid;
else l = mid + 1;
}
if (sum[l].s == t)
{
printf("%d %d %d %d\n", a, b, sum[l].c, sum[l].d);
return 0;
}
}
}
}前缀和:
一维前缀和:
图解分析:

模板:
int n, m;
int sum[N];
void Prefix_and(int a[])
{
for (int i = 1; i <= n; i ++ ) sum[i] = sum[i - 1] + a[i];
}
int Sum(int l, int r)
{
return sum[r] - sum[l - 1];
}一维前缀和例题(C++版):
Acwing795.前缀和

#include <iostream>
using namespace std;
const int N = 100010;
int n, m;
int sum[N];
void Prefix_and(int a[])
{
for (int i = 1; i <= n; i ++ ) sum[i] = sum[i - 1] + a[i];
}
int Sum(int l, int r)
{
return sum[r] - sum[l - 1];
}
int main()
{
cin >> n >> m;
int a[N];
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
Prefix_and(a);
while (m --)
{
int l, r;
cin >> l >> r;
cout << Sum(l, r) << endl;;
}
}二维前缀和:
图解分析:
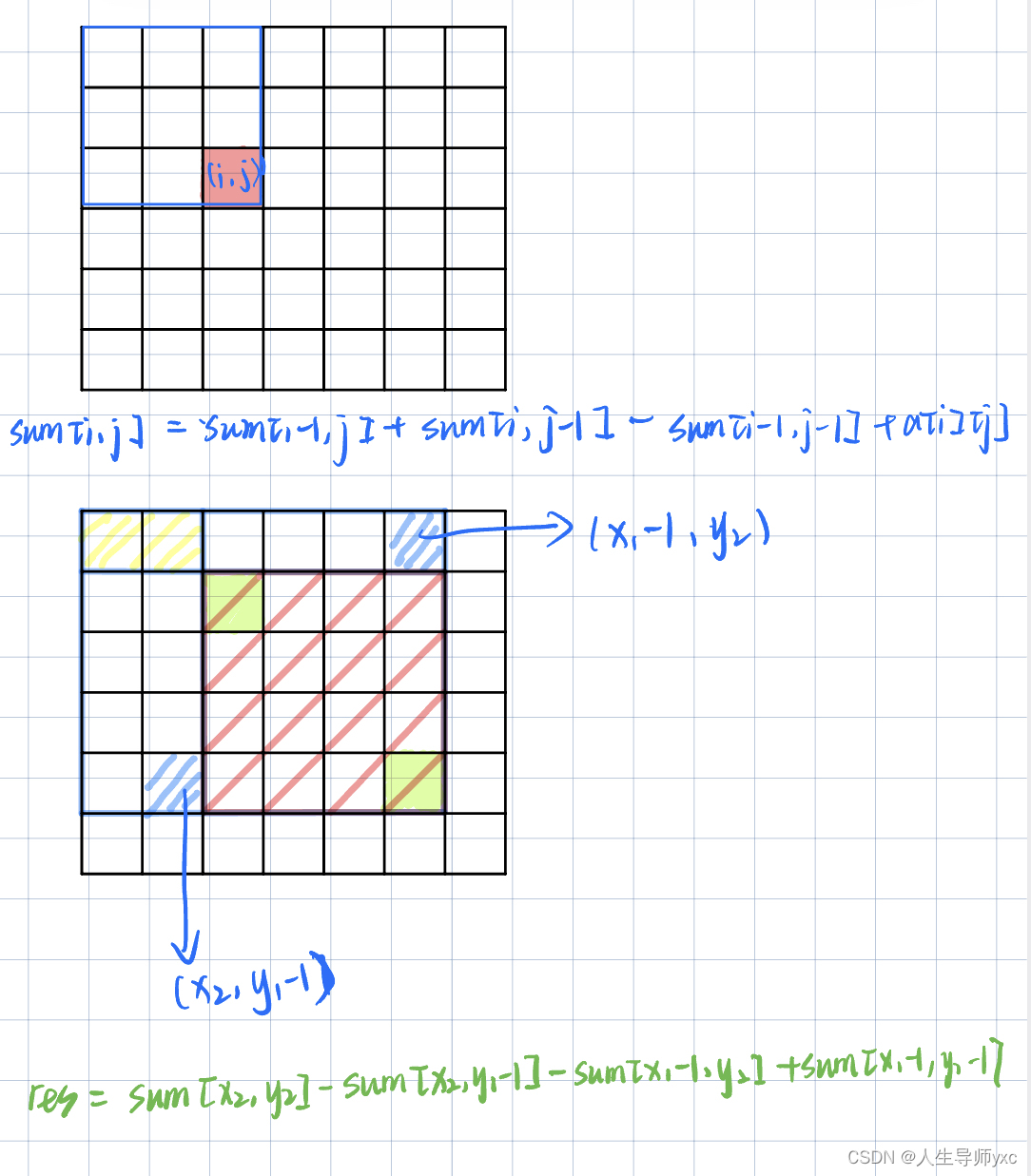
模板:
int n, m;
int sum[N][N];
void Prefix_and(int a[N][N])
{
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];
}
int Sum(int x1, int y1, int x2, int y2)
{
int res = sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1];
return res;
}二维前缀和例题(C++版):
Acwing796.子矩阵的和

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int sum[N][N];
void Prefix_and(int a[N][N])
{
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];
}
int Sum(int x1, int y1, int x2, int y2)
{
int res = sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1];
return res;
}
int main()
{
int q;
cin >> n >> m >> q;
int a[N][N];
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
cin >> a[i][j];
Prefix_and(a);
while (q --)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << Sum(x1, y1, x2, y2) << endl;
}
}