6.5 Batch Normalization

news2024/11/26 8:21:27

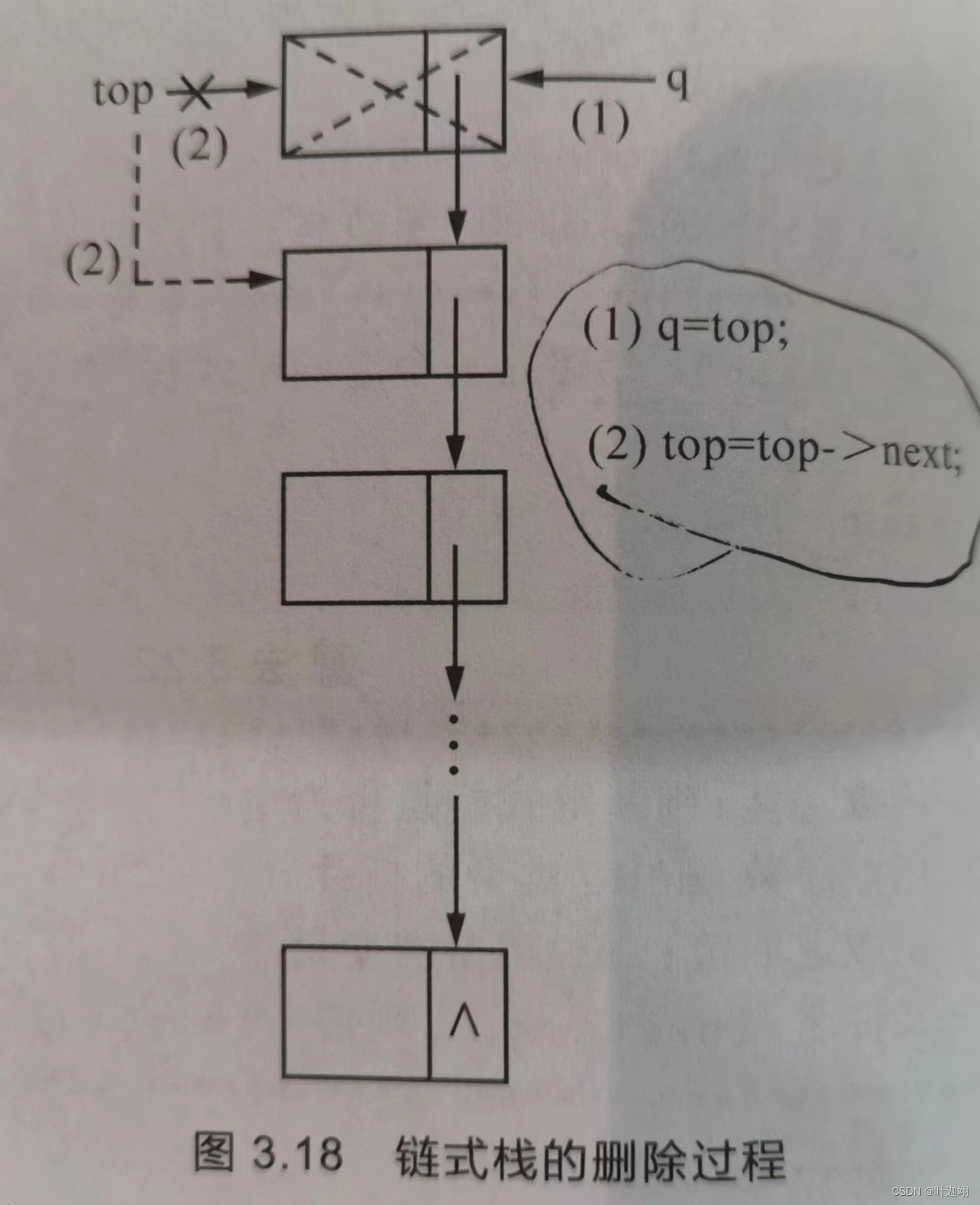
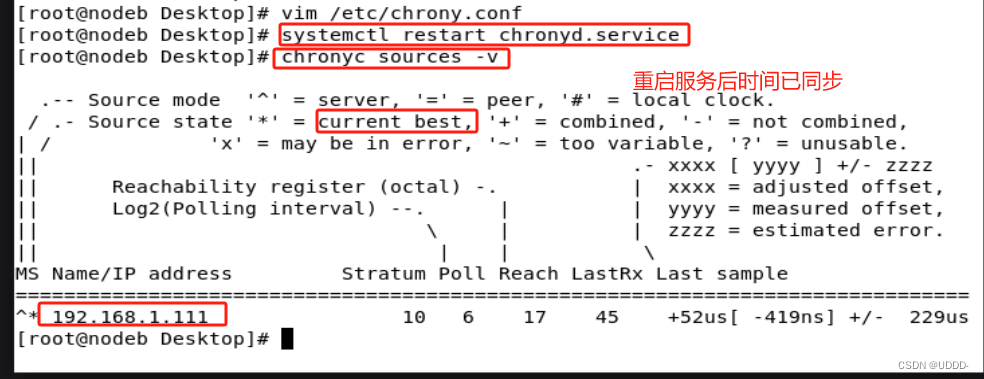
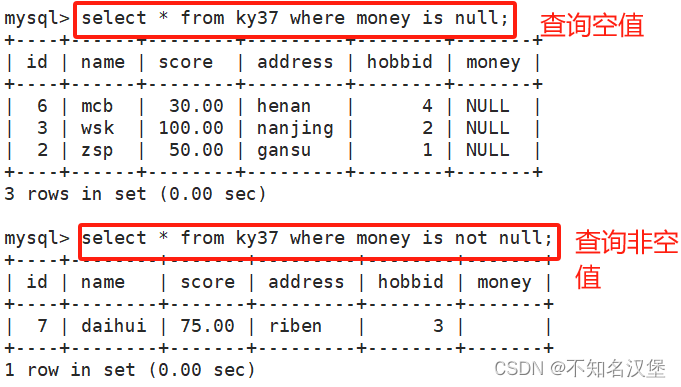
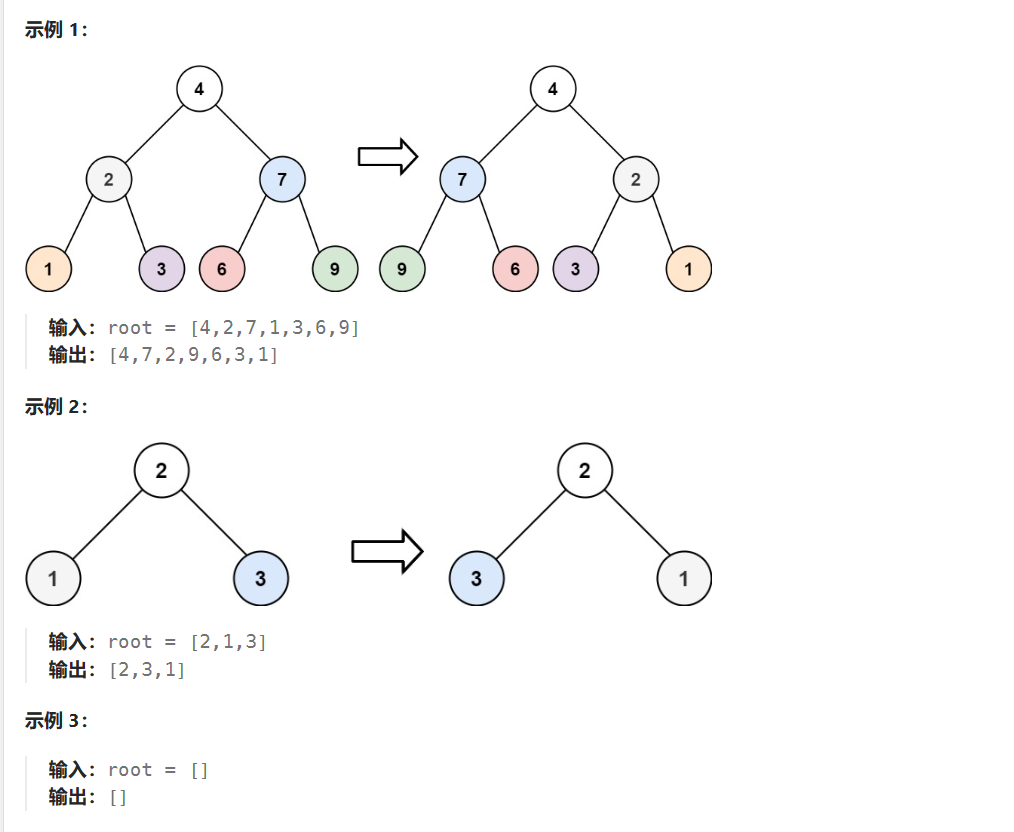
在训练神经网络时，往往需要标准化（normalization）输入数据，使得网络的训练更加快速和有效。

然而SGD（随机梯度下降）等学习算法会在训练中不断改变网络的参数，隐藏层的激活值的分布会因此发生变化，而这一种变化就称为内协变量偏移（Internal Covariate Shift，ICS）。

为了解决ICS问题，批标准化（Batch Normalization）固定激活函数的输入变量的均值和方差，使得网络的训练更快。

除了加速训练这一优势，Batch Normalization还具备其他功能：

①应用了Batch Normalization的神经网络在反向传播中有着非常好的梯度流；

这样，神经网络对权重的初值和尺度依赖减少，能够使用更高的学习率，还降低了不收敛的风险。

②Batch Normalization还具有正则化的作用，Dropout也就不再需要了。

③Batch Normalization让深度神经网络使用饱和非线性函数成为可能。

一、Batch Normalization的实现方式

Batch Normalization在训练时，用当前训练批次的数据单独的估计每一激活值 x⁽ᴷ⁾ 的均值和方差。为了方便，我们接下来只关注某一个激活值 x⁽ᴷ⁾ ，并将 k 省略掉，现定义当前批次为具有 m 个激活值的 β：

β = Xi （i=1，...，m）

首先，计算当前批次激活值的均值和方差：

然后用计算好的均值 $\mu _{\beta }$ 和方差 δ_β ² 标准化这一批次的激活值 $x_{i}$ ，得到 $\hat{x}_{i}$ ，为了避免除0， $\epsilon$ 被设置为一个非常小的数字，在PyTorch中，默认设置为 le - 5：

这样，我们就固定了当前批次 β 的分布，使得其服从均值为0、方差为1的高斯分布。

但是标准化有可能会降低模型的表达能力，因为网络中的某些隐藏层很有可能就是需要输入数据是非标准化分布的，所以Batch Normalization对标准化的变量 $x_{i}$ 加了一步防射变化

$y _{i}$ = y $\hat{x}_{i}$ + β，

添加的两个参数 $\gamma$ 和 β 用于恢复网络的表示能力，它们和网络原本的权重一起训练。

在PyTorch中，β 初始化为0，而 $\gamma$ 则从均匀分布随机采样。当时，标准化的激活值则完全恢复成原始值，这完全由训练中的网络自行决定。

训练完毕后， $\gamma$ 和 β 作为中间状态被保存下来。

在PyTorch的实现中，Batch Normalization在训练时还会计算移动平均化的均值和方差：

running_mean = （1 - momentum）· running_mean + momentum · $\mu _{\beta }$

running_var = （1-momentum）· running_var + momentum · δ_β ²

momentum默认为0.1，running_mean 和 running_var在训练完毕后保留，用于模型验证。

Batch Normalization在训练完毕后，保留了两个参数 β 和 $\gamma$ ，以及两个变量running_mean和running_var。

在模型做验证时，做如下变换：

二、Batch Normalization的使用方法

在PyTorch中，nn.BatchNorm1d 提供了Batch Normalization的实现，同样地，它也被当作神经网络中的层使用。

它有两个十分关键的参数：

①num_features确定特征的数量；

②affine决定Batch Normalization是否使用仿射映射。

1、代码示例：

（1）实例化一个BatchNorm1d对象，它接收特征数量 num_features = 5 的数据，所以模型的两个中间变量 running_mean 和 running_var 就会被初始化为5维的向量，用于统计移动平均化的均值和方差。

（2）输出这两个变量的数据，可以很直观地看到它们的初始化方式。

（3）从标准高斯分布采样了一些数据然后提供给Batch Normalization层。

（4）输出变化后的 running_mean 和 running_var，可以发现它们的数值发生了一些变化但是基本维持了标准高斯分布的均值方差数值。

（5）验证了如果我们将模型设置为eval模式，这两个变量不会发生任何变化。

输出：

上面代码（1）设置了affine = False，也就是不对标准化后的数据采用仿射变化，关于仿射变换的两个参数 β 和 y 在 BatchNorm1d 中称为 weight 和 bias。

代码（2）输出了这两个变量，显然因为我们关闭了仿射变化，所以这两个变量被设置为None。

2、代码示例

下面设置 affine = True，然后输出 m_affine.weight、m_affine.bias，可以看到，y 从均匀分布 U（0，1）随机采样，而 β 被初始化为0。

输出：

应当注意，m_affine.weight 和 m_affine.bias的类型均为Parameter。

也就是说它们和线性模型的权重是一种类型，参与模型的训练，而running_mean 和 running_var 的类型为Tensor，这样的变量在PyTorch中称为buffer。

buffer不影响模型的训练，仅作为中间变量更新和保存。

四、代码

import torch
from torch import nn

m = nn.BatchNorm1d(num_features=5,affine=False)
print("BEFORE:")
print("running_mean:",m.running_mean)
print("running_var:",m.running_var)

for _ in range(100):
    input = torch.randn(20,5)
    output= m(input)

print("AFTER:")
print("running_mean:",m.running_mean)
print("running_var:",m.running_var)

m.eval()
for _ in range(100):
    input = torch.randn(20,5)
    output = m(input)

print("EVAL:")
print("running_mean:",m.running_mean)
print("running_var:",m.running_var)

#########################################

print("no affine,gamma:",m.weight)
print("no affine,beta:",m.bias)

m_affine = nn.BatchNorm1d(num_features=5,affine=True)
print("")
print("with affine,gamma:",m_affine.weight,type(m_affine.weight))
print("with affine,beta:",m_affine.bias,type(m_affine.bias))

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1561261.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！