文章目录
- 4. 后继屈服条件
- 4.1 后继屈服条件
- 4.2 强化模型
- 4.2.1 等向强化模型
- 4.2.2 随动强化模型
- 4.2.3 两种强化模型的讨论
4. 后继屈服条件
4.1 后继屈服条件
上一章节的屈服条件是在当材料未经受任何塑性变形时且在载荷作用下材料第一次进入屈服应该满足的条件(也叫初始屈服条件),那么对于材料进入屈服后继续加载,材料性能会遵循什么样的规则呢?
回顾在材料的单向拉伸力学试验的讨论中,由下图1应力应变曲线,其中下图1左图为多晶材料的应力应变曲线,存在包晶格效应,表现为一个方向强化对应另一个方向的弱化,右图则没有。不管时哪种应力应变曲线,当材料受到载荷作用时,应力应变先线性增加,到达 σ s \sigma_s σs时,材料进入屈服,随着载荷的进一步增加,应力应变曲线从A点到达M点,此时,如果卸去全部载荷,应力应变遵循MO’卸载到应力为零,再重新加载时,材料应力应变就会沿O’MD变化。那么就相当于M点的应力 σ s ′ \sigma_s^{'} σs′变成了新的屈服极限了,称此为后继屈服点。
同时,材料从OAM到M和从O’M到M,M的应力应变状态是一致的,因此材料载荷连续增加从A增加到M,就可以理解为考虑了塑性变形后材料再从O’M增加到M。那么后继屈服条件方程形式与初始屈服条件应为一致,只需把
σ
s
\sigma_s
σs换成
σ
s
′
\sigma_s^{'}
σs′即可。

图 1 加载 / 卸载应力应变曲线 图1\quad 加载/卸载应力应变曲线 图1加载/卸载应力应变曲线
对于一般应力状态( σ i j \sigma_{ij} σij),在初始屈服之后遵循规则同单向拉伸一致,即在一般应力状态在初始屈服之后同样满足后继屈服条件,与单向应力状态不同的是,此时后继屈服不是一个点,而是一个面。
我们可以这么想,AM阶段是弹性,那么M就是AM的初始屈服条件了,那么显然可以参考初始屈服条件的形式,此时后继屈服条件也可以写成如下形式
f
(
σ
i
j
,
ξ
β
)
=
0
(1)
f(\sigma_{ij},\xi_\beta)=0\tag{1}
f(σij,ξβ)=0(1)
称
ξ
β
\xi_\beta
ξβ为内变量,与材料的塑性变形历史相关。当
ξ
β
=
0
\xi_\beta=0
ξβ=0时,上式就会化为上章节的屈服条件。随着
ξ
β
\xi_\beta
ξβ的变化,后继屈服条件的大小、形状和位置都可能会产生变化。因此后继屈服面是一系列的曲面。
当应力位于屈服曲面内时,应力和应变呈现弹性特点,不产生新的塑性变形,因此
ξ
β
\xi_\beta
ξβ不变化,当应力位于屈服曲面上
,当载荷继续增加时,应力的变化会增加新的塑性变形,因此会引起内变量的改变,此时会形成新的屈服曲面
f
(
σ
i
j
+
d
σ
i
j
,
ξ
β
+
d
ξ
β
)
=
f
(
σ
i
j
,
ξ
β
)
+
d
f
(
σ
i
j
+
d
σ
i
j
,
ξ
β
+
d
ξ
β
)
=
0
(2)
f(\sigma_{ij}+d\sigma_{ij},\xi_\beta+d\xi_\beta)=f(\sigma_{ij},\xi_\beta)+df(\sigma_{ij}+d\sigma_{ij},\xi_\beta+d\xi_\beta)=0\tag{2}
f(σij+dσij,ξβ+dξβ)=f(σij,ξβ)+df(σij+dσij,ξβ+dξβ)=0(2)
那么,有
d
f
(
σ
i
j
+
d
σ
i
j
,
ξ
β
+
d
ξ
β
)
=
∂
f
∂
σ
i
j
d
σ
i
j
+
∂
f
∂
ξ
β
d
ξ
β
=
0
(3)
df(\sigma_{ij}+d\sigma_{ij},\xi_\beta+d\xi_\beta)=\frac{\partial f}{\partial \sigma_{ij}}d\sigma_{ij}+\frac{\partial f}{\partial \xi_{\beta}}d\xi_{\beta}=0\tag{3}
df(σij+dσij,ξβ+dξβ)=∂σij∂fdσij+∂ξβ∂fdξβ=0(3)
这就是屈服条件的一致性条件。
4.2 强化模型
观察应力应变曲线,材料在超过屈服后有强化阶段,因此后继屈服条件总是与初始屈服条件不一样,为了描述这种材料行为,人们建立了多种强化模型,其中最典型的有等向强化模型和随动强化模型。
4.2.1 等向强化模型
在等向强化模型中,材料进入塑性后在一个方向的应力强化,在相反方向同样进行了强化,同时认为两者的同量强化,即M点和M’点应力绝对值相等。这相当于后继屈服曲面在应力空间中是初始屈服曲面的相似扩大,中心位置和形状都与初始屈服曲面一致。

图
2
等向强化的加载
/
卸载应力应变曲线
图2\quad 等向强化的加载/卸载应力应变曲线
图2等向强化的加载/卸载应力应变曲线
回顾初始屈服条件,其方程具备以下形式
f
(
σ
i
j
)
=
f
∗
(
σ
i
j
)
−
k
=
0
(4)
f(\sigma_{ij})=f^*(\sigma_{ij})-k=0\tag{4}
f(σij)=f∗(σij)−k=0(4)
那么等向强化模型的后继屈服条件方程具备以下形式
f
(
σ
i
j
,
ξ
β
)
=
f
∗
(
σ
i
j
)
−
k
(
ξ
β
)
=
0
(5)
f(\sigma_{ij},\xi_\beta)=f^*(\sigma_{ij})-k(\xi_\beta)=0\tag{5}
f(σij,ξβ)=f∗(σij)−k(ξβ)=0(5)
一般常将内变量
ξ
β
\xi_\beta
ξβ取为等效塑性应变增量
d
ξ
β
=
2
3
d
ε
k
l
p
d
ε
k
l
p
(6)
d\xi_\beta=\sqrt{\frac{2}{3}d\varepsilon_{kl}^pd\varepsilon_{kl}^p}\tag{6}
dξβ=32dεklpdεklp(6)
或者塑性功增量
d
ξ
β
=
σ
k
l
d
ε
k
l
p
=
d
W
p
(7)
d\xi_\beta=\sigma_{kl}d\varepsilon_{kl}^p=dW^p\tag{7}
dξβ=σkldεklp=dWp(7)
并且,当
ξ
β
=
0
\xi_\beta=0
ξβ=0时,式(4)就退化为式(3),即
k
(
ξ
β
=
0
)
=
k
k(\xi_\beta=0)=k
k(ξβ=0)=k。
以Mise屈服条件为例,回顾Mise屈服条件,有
σ
‾
−
σ
s
=
0
\overline\sigma-\sigma_s=0
σ−σs=0,那么对应的后继屈服条件方程为
f
(
σ
i
j
,
ξ
β
)
=
σ
‾
−
k
(
ξ
β
)
=
0
k
(
ξ
β
=
0
)
=
σ
s
(8)
\begin{aligned} f(\sigma_{ij},\xi_\beta)=\overline\sigma-k(\xi_\beta)=0\\ k(\xi_\beta=0)=\sigma_s \end{aligned}\tag{8}
f(σij,ξβ)=σ−k(ξβ)=0k(ξβ=0)=σs(8)
当内变量
ξ
β
\xi_\beta
ξβ取为等效塑性应变增量,
k
(
ξ
β
)
k(\xi_\beta)
k(ξβ)可以有单向拉伸试验确定。事实上当
d
ξ
β
=
d
ε
1
p
d\xi_\beta=d\varepsilon_{1}^p
dξβ=dε1p
在单向拉伸试验中,主应力方向1为拉伸方向,在试验过程中始终不变,因此
ξ
β
=
∫
d
ε
1
p
=
ε
1
p
\xi_\beta=\int d\varepsilon_{1}^p=\varepsilon_{1}^p
ξβ=∫dε1p=ε1p
k
(
ξ
β
)
=
k
(
ε
1
p
)
k(\xi_\beta)=k(\varepsilon_{1}^p)
k(ξβ)=k(ε1p)确定过程如下图3,下图3左图为单向拉伸应力应变曲线,下图3右图为单向拉伸应力应变曲线去除弹性应变分量,其中在图3中左图切线斜率就是模量E’,图3中右图切线斜率就是前文中提到过的h,不难知道其实
k
(
ε
1
p
)
=
h
k(\varepsilon_{1}^p)=h
k(ε1p)=h。
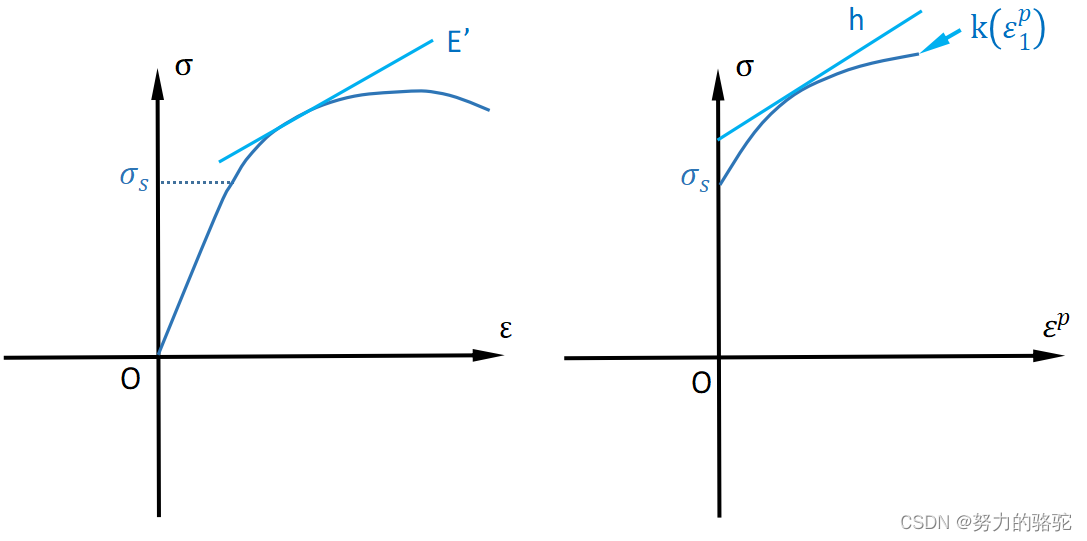
图 3 单向拉伸试验应力应变曲线 图3\quad 单向拉伸试验应力应变曲线 图3单向拉伸试验应力应变曲线
4.2.2 随动强化模型
等向强化模型不符合很多材料的力学特征,很多材料存在一个方向上强化,其相反方向弱化的特点(即包氏效应),因此对此提出随动强化模型。随动强化模型假设材料一个方向上强化,其相反方向弱化同等数量,即如下图所示,其后继屈服点M与反方向后继屈服点M’的差值保持不变,等于2 σ s \sigma_s σs,那么不难发现其实在应力空间中,就是初始屈服曲面的位置平动形成一系列随动强化模型下的后继屈服曲面。

图
4
随动强化的加载
/
卸载应力应变曲线
图4\quad 随动强化的加载/卸载应力应变曲线
图4随动强化的加载/卸载应力应变曲线
那么后继屈服条件的方程为
f
(
σ
i
j
,
ξ
β
)
=
f
∗
(
σ
i
j
−
α
i
j
)
−
k
=
0
(9)
f(\sigma_{ij},\xi_\beta)=f^*(\sigma_{ij}-\alpha_{ij})-k=0\tag{9}
f(σij,ξβ)=f∗(σij−αij)−k=0(9)
其中
α
i
j
\alpha_{ij}
αij为内变量
ξ
β
\xi_\beta
ξβ的分量形式,当
α
i
j
=
0
\alpha_{ij}=0
αij=0时,上式退化为初始屈服条件方程,因此其意义就是表示屈服曲面中心平移的度量。不同的
α
i
j
\alpha_{ij}
αij演化规律又对应不同的随动强化模型,典型如下
(1)线性随动强化模型
α
˙
i
j
=
c
ε
˙
i
j
p
(10)
\dot\alpha_{ij}=c\dot\varepsilon_{ij}^p\tag{10}
α˙ij=cε˙ijp(10)
式中c是一个材料相关常数。式(9)其实也可以写成增量的形式
d
α
i
j
=
c
d
ε
i
j
p
(10’)
d\alpha_{ij}=cd\varepsilon_{ij}^p\tag{10'}
dαij=cdεijp(10’)
观察式(10),此式中为各分量形式,因此能够直接积分(塑性等效应变不能直接积分,因为在变形过程中方向会有变化),得到
α
i
j
=
c
ε
i
j
p
(11)
\alpha_{ij}=c\varepsilon_{ij}^p\tag{11}
αij=cεijp(11)
代入式(9),那么有
f
(
σ
i
j
,
ξ
β
)
=
f
∗
(
σ
i
j
−
c
ε
i
j
p
)
−
k
=
0
(12)
f(\sigma_{ij},\xi_\beta)=f^*(\sigma_{ij}-c\varepsilon_{ij}^p)-k=0\tag{12}
f(σij,ξβ)=f∗(σij−cεijp)−k=0(12)
以Mise屈服条件为例,其方程为
f
(
σ
i
j
,
ξ
β
)
=
f
∗
(
σ
i
j
−
c
ε
i
j
p
)
−
k
=
σ
‾
(
σ
i
j
−
c
ε
i
j
p
)
−
k
=
0
(13)
f(\sigma_{ij},\xi_\beta)=f^*(\sigma_{ij}-c\varepsilon_{ij}^p)-k=\overline\sigma(\sigma_{ij}-c\varepsilon_{ij}^p)-k=0\tag{13}
f(σij,ξβ)=f∗(σij−cεijp)−k=σ(σij−cεijp)−k=0(13)
其中等效应力
σ
‾
\overline\sigma
σ如下所示
σ
‾
(
σ
i
j
−
c
ε
i
j
p
)
=
3
2
(
s
i
j
−
c
ε
i
j
p
)
(
s
i
j
−
c
ε
i
j
p
)
(14)
\overline\sigma(\sigma_{ij}-c\varepsilon_{ij}^p)=\sqrt{\frac{3}{2}(s_{ij}-c\varepsilon_{ij}^p)(s_{ij}-c\varepsilon_{ij}^p)}\tag{14}
σ(σij−cεijp)=23(sij−cεijp)(sij−cεijp)(14)
其中
k
k
k就是
σ
s
\sigma_s
σs。
在简单拉伸时,
σ
i
j
、
s
i
j
、
ε
i
j
p
\sigma_{ij}、s_{ij}、\varepsilon_{ij}^p
σij、sij、εijp如下非零项
σ
11
=
σ
,
s
11
=
σ
11
−
σ
m
=
2
3
σ
,
s
22
=
s
33
=
−
1
3
σ
;
ε
11
p
=
ε
p
,
ε
22
p
=
ε
33
p
=
−
1
2
ε
p
(
塑性时泊松比为
1
2
)
\sigma_{11} = \sigma,s_{11} = \sigma_{11} - \sigma_{m}=\frac{2}{3}\sigma, s_{22}=s_{33}=-\frac{1}{3}\sigma;\\ \varepsilon_{11}^p=\varepsilon^p,\varepsilon_{22}^p=\varepsilon_{33}^p=-\frac{1}{2}\varepsilon^p(塑性时泊松比为\frac{1}{2})
σ11=σ,s11=σ11−σm=32σ,s22=s33=−31σ;ε11p=εp,ε22p=ε33p=−21εp(塑性时泊松比为21)
代入式(14),有
σ
‾
=
3
2
(
s
i
j
−
c
ε
i
j
p
)
(
s
i
j
−
c
ε
i
j
p
)
=
3
2
[
(
s
11
−
c
ε
11
p
)
2
+
(
s
22
−
c
ε
22
p
)
2
+
(
s
33
−
c
ε
33
p
)
2
]
=
3
2
[
(
2
3
σ
−
c
ε
p
)
2
+
(
−
1
3
σ
+
c
⋅
1
2
ε
p
)
2
+
(
−
1
3
σ
+
c
⋅
1
2
ε
p
)
2
]
=
3
2
(
2
3
σ
2
−
2
σ
c
ε
p
+
3
2
c
2
⋅
(
ε
p
)
2
)
=
3
2
⋅
2
3
(
σ
2
−
3
σ
c
ε
p
+
9
4
c
2
⋅
(
ε
p
)
2
)
=
σ
−
3
2
c
⋅
ε
p
(15)
\begin{aligned} \overline\sigma&=\sqrt{\frac{3}{2}(s_{ij}-c\varepsilon_{ij}^p)(s_{ij}-c\varepsilon_{ij}^p)}\\ &=\sqrt{\frac{3}{2}[(s_{11}-c\varepsilon_{11}^p)^2+(s_{22}-c\varepsilon_{22}^p)^2+(s_{33}-c\varepsilon_{33}^p)^2]}\\ &=\sqrt{\frac{3}{2}[(\frac{2}{3}\sigma-c\varepsilon^p)^2+(-\frac{1}{3}\sigma+c\cdot\frac{1}{2}\varepsilon^p)^2+(-\frac{1}{3}\sigma+c\cdot\frac{1}{2}\varepsilon^p)^2]}\\ &=\sqrt{\frac{3}{2}(\frac{2}{3}\sigma^2-2\sigma c\varepsilon^p+\frac{3}{2}c^2\cdot(\varepsilon^p)^2)}\\ &=\sqrt{\frac{3}{2}\cdot\frac{2}{3}(\sigma^2-3\sigma c\varepsilon^p+\frac{9}{4}c^2\cdot(\varepsilon^p)^2)}\\ &=\sigma-\frac{3}{2}c\cdot\varepsilon^p \end{aligned}\tag{15}
σ=23(sij−cεijp)(sij−cεijp)=23[(s11−cε11p)2+(s22−cε22p)2+(s33−cε33p)2]=23[(32σ−cεp)2+(−31σ+c⋅21εp)2+(−31σ+c⋅21εp)2]=23(32σ2−2σcεp+23c2⋅(εp)2)=23⋅32(σ2−3σcεp+49c2⋅(εp)2)=σ−23c⋅εp(15)
将上式代入式(13),有
f
(
σ
i
j
,
ξ
β
)
=
σ
‾
(
σ
i
j
−
c
ε
i
j
p
)
−
k
=
σ
−
3
2
c
⋅
ε
p
−
σ
s
=
0
(16)
f(\sigma_{ij},\xi_\beta)=\overline\sigma(\sigma_{ij}-c\varepsilon_{ij}^p)-k=\sigma-\frac{3}{2}c\cdot\varepsilon^p-\sigma_s=0\tag{16}
f(σij,ξβ)=σ(σij−cεijp)−k=σ−23c⋅εp−σs=0(16)
即
σ
=
σ
s
+
3
2
c
⋅
ε
p
(17)
\sigma=\sigma_s+\frac{3}{2}c\cdot\varepsilon^p\tag{17}
σ=σs+23c⋅εp(17)
前面章节,由简单拉伸的应力应变曲线
σ
=
σ
s
+
h
ε
p
(18)
\sigma=\sigma_s+h\varepsilon^p\tag{18}
σ=σs+hεp(18)
得出
c
=
2
3
h
c=\frac{2}{3}h
c=32h。
(2)Ziegler模型
α
˙
i
j
=
η
˙
(
σ
i
j
−
α
i
j
)
(
η
˙
>
0
)
(19)
\dot\alpha_{ij}=\dot\eta(\sigma_{ij}-\alpha_{ij})(\dot\eta\gt0)\tag{19}
α˙ij=η˙(σij−αij)(η˙>0)(19)
其增量型方程为
d
α
i
j
=
d
η
⋅
(
σ
i
j
−
α
i
j
)
(
d
η
>
0
)
(19’)
d\alpha_{ij}=d\eta\cdot(\sigma_{ij}-\alpha_{ij})(d\eta\gt0)\tag{19'}
dαij=dη⋅(σij−αij)(dη>0)(19’)
上式代入一致性条件,可得
∂
f
∂
(
σ
i
j
−
α
i
j
)
⋅
∂
(
σ
i
j
−
α
i
j
)
∂
σ
i
j
d
σ
i
j
+
∂
f
∂
(
σ
i
j
−
α
i
j
)
⋅
∂
(
σ
i
j
−
α
i
j
)
∂
α
i
j
d
α
i
j
=
∂
f
∂
(
σ
i
j
−
α
i
j
)
⋅
1
⋅
d
σ
i
j
+
∂
f
∂
(
σ
i
j
−
α
i
j
)
⋅
−
1
⋅
d
α
i
j
=
0
(20)
\begin{aligned} &\frac{\partial f}{\partial (\sigma_{ij}-\alpha_{ij})}\cdot\frac{\partial (\sigma_{ij}-\alpha_{ij})}{\partial \sigma_{ij}}d\sigma_{ij}+\frac{\partial f}{\partial (\sigma_{ij}-\alpha_{ij})}\cdot\frac{\partial (\sigma_{ij}-\alpha_{ij})}{\partial \alpha_{ij}}d\alpha_{ij}\\ =&\frac{\partial f}{\partial (\sigma_{ij}-\alpha_{ij})}\cdot1\cdot d\sigma_{ij}+\frac{\partial f}{\partial (\sigma_{ij}-\alpha_{ij})}\cdot -1 \cdot d\alpha_{ij}=0 \end{aligned}\tag{20}
=∂(σij−αij)∂f⋅∂σij∂(σij−αij)dσij+∂(σij−αij)∂f⋅∂αij∂(σij−αij)dαij∂(σij−αij)∂f⋅1⋅dσij+∂(σij−αij)∂f⋅−1⋅dαij=0(20)
随动强化模型后继屈服条件的方程有
f
(
σ
i
j
,
ξ
β
)
=
f
∗
(
σ
i
j
−
α
i
j
)
−
k
=
0
f(\sigma_{ij},\xi_\beta)=f^*(\sigma_{ij}-\alpha_{ij})-k=0
f(σij,ξβ)=f∗(σij−αij)−k=0
因此,有
∂
f
∂
(
σ
i
j
−
α
i
j
)
=
∂
f
∂
σ
i
j
=
∂
f
∗
∂
σ
i
j
(21)
\frac{\partial f}{\partial (\sigma_{ij}-\alpha_{ij})}=\frac{\partial f}{\partial \sigma_{ij}}=\frac{\partial f^*}{\partial \sigma_{ij}}\tag{21}
∂(σij−αij)∂f=∂σij∂f=∂σij∂f∗(21)
将上式代入式(20),有
∂
f
∗
∂
σ
i
j
d
σ
i
j
−
∂
f
∗
∂
σ
i
j
d
α
i
j
=
∂
f
∗
∂
σ
i
j
(
d
σ
i
j
−
d
α
i
j
)
=
0
(22)
\frac{\partial f^*}{\partial \sigma_{ij}} d\sigma_{ij}-\frac{\partial f^*}{\partial \sigma_{ij}}d\alpha_{ij}=\frac{\partial f^*}{\partial \sigma_{ij}}( d\sigma_{ij}-d\alpha_{ij})=0\tag{22}
∂σij∂f∗dσij−∂σij∂f∗dαij=∂σij∂f∗(dσij−dαij)=0(22)
将式(19’)代入上式,则
∂
f
∗
∂
σ
i
j
(
d
σ
i
j
−
d
α
i
j
)
=
∂
f
∗
∂
σ
i
j
[
d
σ
i
j
−
d
η
⋅
(
σ
i
j
−
α
i
j
)
]
=
0
(23)
\frac{\partial f^*}{\partial \sigma_{ij}}( d\sigma_{ij}-d\alpha_{ij})=\frac{\partial f^*}{\partial \sigma_{ij}}[ d\sigma_{ij}-d\eta\cdot(\sigma_{ij}-\alpha_{ij})]=0\tag{23}
∂σij∂f∗(dσij−dαij)=∂σij∂f∗[dσij−dη⋅(σij−αij)]=0(23)
d
η
=
∂
f
∗
∂
σ
i
j
d
σ
i
j
/
[
∂
f
∗
∂
σ
k
l
(
σ
k
l
−
α
k
l
)
]
(24)
d\eta=\frac{\partial f^*}{\partial \sigma_{ij}} d\sigma_{ij}/[\frac{\partial f^*}{\partial \sigma_{kl}}(\sigma_{kl}-\alpha_{kl})]\tag{24}
dη=∂σij∂f∗dσij/[∂σkl∂f∗(σkl−αkl)](24)
那么,
α
i
j
=
∫
d
η
⋅
(
σ
i
j
−
α
i
j
)
\alpha_{ij}=\int d\eta\cdot(\sigma_{ij}-\alpha_{ij})
αij=∫dη⋅(σij−αij)
同样将上式代入式(13),就可得到相应的后继屈服条件方程
f
(
σ
i
j
,
ξ
β
)
=
σ
‾
(
σ
i
j
−
α
i
j
)
−
k
=
0
f(\sigma_{ij},\xi_\beta)=\overline\sigma(\sigma_{ij}-\alpha_{ij})-k=0
f(σij,ξβ)=σ(σij−αij)−k=0
具体形式先不展开了,因为在暂时用不上。
4.2.3 两种强化模型的讨论
在 π \pi π平面上,两种模型的形象比较,下图中C1为初始Mise屈服条件的屈服曲线,C2为等向强化模型的初始Mise屈服条件的屈服曲线,C3为随动强化模型的初始Mise屈服条件的屈服曲线,其中 α \alpha α为 α i j \alpha_{ij} αij。
图中可以看出等向强化模型对应屈服面等比例扩大,但是中心位置不变,随动强化对应的是中心位置的移动,但是半径不变。
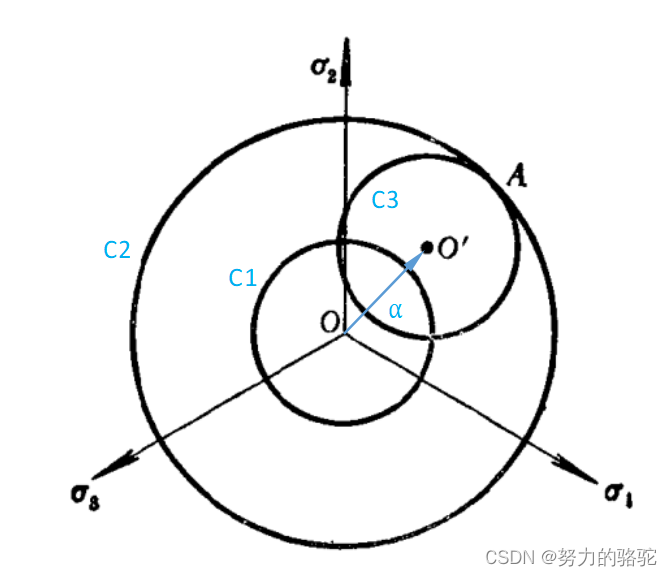
图
5
两种强化模型的屈服曲线(
π
平面)
图5\quad 两种强化模型的屈服曲线(\pi平面)
图5两种强化模型的屈服曲线(π平面)
Ivey曾对铝合金薄圆管进行了拉扭实验,但随着剪应力的增加,整个后继屈服面都向剪应力增加的方向移动,接近于随动强化模型。
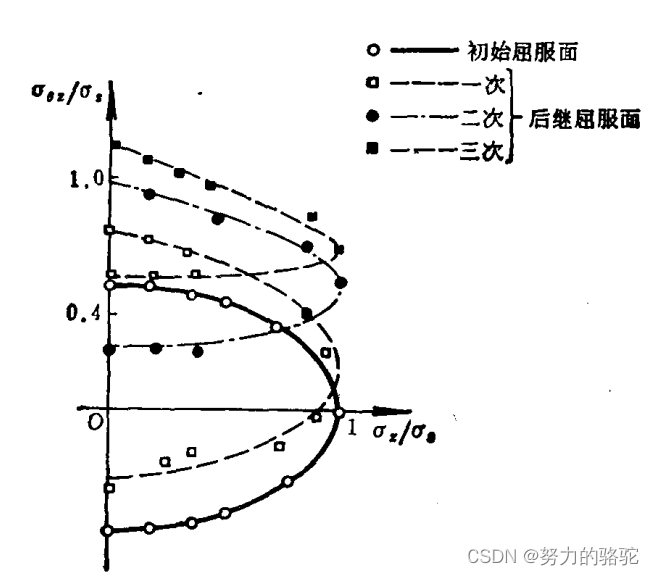
图
6
实验的后继屈服曲线
图6\quad 实验的后继屈服曲线
图6实验的后继屈服曲线