文章目录
- 问题一:2164 - 子结点的数量
- 问题二:2165 - 子结点的数量(2)
- 问题三:1775 - 谁的孙子最多
- 问题四:1776 - 谁的孙子最多II
问题一:2164 - 子结点的数量
类型:树
题目描述:
给定一棵树中的若干父结点和子结点的关系描述(结点 1 是树根),请问该树中,每个结点有多少个子结点。
比如:读入父子关系如下,先读入父结点,再读入子结点。
1 2
2 3
2 4
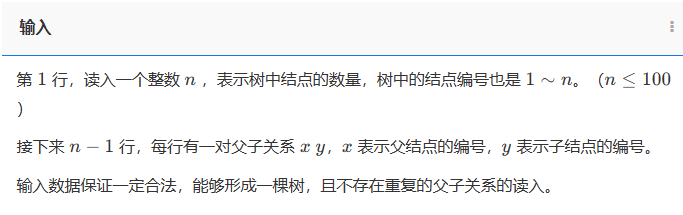
输入:
第 1 行,读入一个整数 n ,表示树中结点的数量,树中的结点编号也是 1∼n。(n≤100)
接下来n−1 行,每行有一对父子关系 x y,x 表示父结点的编号,y 表示子结点的编号。
输入数据保证一定合法,能够形成一棵树,且不存在重复的父子关系的读入。
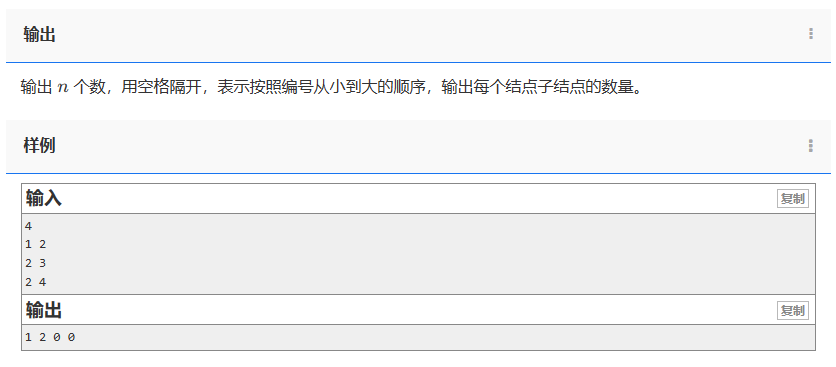
输出:
输出 n 个数,用空格隔开,表示按照编号从小到大的顺序,输出每个结点子结点的数量。
样例:
输入:
4
1 2
2 3
2 4
输出:
1 2 0 0

解题思路:
正如你所想的一样,接下来让我们代入“凶手”的第一视角,看看是如何干掉这道题的。

首先认真并完整的读完这道题,发现这道题好简单但是好像没看懂。

没关系,没有什么可以难到我,桀 ~ 桀 ~ 桀 ~
“先来提取一些有用的知识吧。”,说着就将目光移动到了输入上。
- 读取一个整数n,n表示树中节点的数量。比如输入4,那么就有1,2,3,4这四个节点,并且1是根节点。
- 接下来又读取了n-1行的数据,那么我们循环的表达式应该是:for(int i=1;i<=n-1;i++)。
- 然后每一行都有一对x,y。x是父节点,y是子节点。
- 数据合法,那么不用考虑其他情况。

- 输出只有一行,输出n个数,用空格隔开,那么就是:
for(int i=1;i<=n;i++){
cout<<输出的数<<" ";
}
- 需要输出的是每个节点的子节点的数量。
“嘶~,怎么知道子节点的数量呢?”

“不急,看看样例怎么回事。”
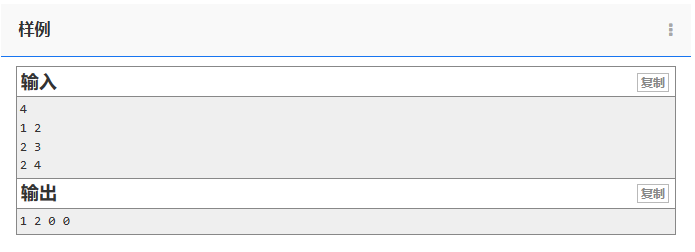
分析一下这个样例。
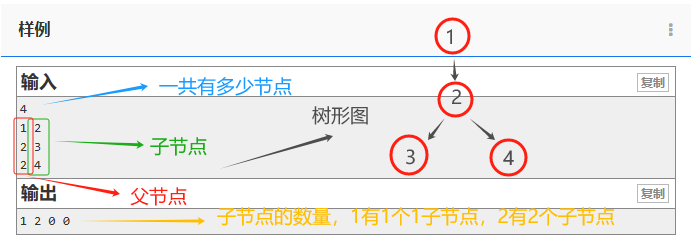
“等等,好像发现了解题的关键。”
“因为题目保证x是父节点,而y是子节点。因此从根开始输入1在前面,2在后面;2在前面,3在后面;2在前面,4在后面。”
“那这里为什么没有3和4在前面的情况呢?因为3和4没有子节点!既然连孩子都没有,他能当父亲吗?”
“很显然是不能的,所以心机之蛙一直摸你肚子!!!”

“这个y其实是一个烟雾弹,我们只需要统计一个节点当了几次父亲就能知道它有几个子节点,即x出现的次数。”
“统计的方法也很简单,数组计数法。首先将数组全部初始化为0,数组的下标就是节点的位置。比如数组[1]就是1节点,数组[2]就是2节点;当x出现一次,那么数组[x]就+1。”
“既然分析清楚,那就开始动手吧!”。
1.分析问题
3. 已知:一棵树中的若干父节点和子节点的关系描述 (x一定是y的父)。
4. 未知:每个节点子节点的数量 。
5. 关系:数组计数法 。
2.定义变量
- n:树中节点总数。
- a[110]:大小为110的数组,用于存储每个节点的子节点计数。数组元素 a[i] 对应于节点 i 的子节点数量。
// 二、数据定义
int n, a[110] = {}, x, y; // n:节点总数;a[]:子节点计数数组;x, y:输入的父节点与子节点关系
3.输入数据
从标准输入(键盘)读取以下信息:
- n:树中节点总数。
- 一系列父节点与子节点关系:逐行读取 x 和 y,表示节点 x 是节点 y 的父节点。
// 读取并处理父节点与子节点关系
for (int i = 1; i < n; i++) {
cin >> x >> y; // 输入关系:节点x是节点y的父节点
a[x]++; // 更新数组a:节点x的子节点计数加1
}
4.数据计算
遍历数组 a,对于每个索引 i(即每个节点),直接输出其对应的子节点计数 a[i]。
// 四、数据计算与输出
// 直接输出数组a中的子节点计数,即每个节点的子节点数量
for (int i = 1; i <= n; i++) {
cout << a[i] << " "; // 输出节点i的子节点数量,后跟一个空格
}
5.输出结果
完整代码如下:
#include <iostream>
using namespace std;
int main() {
// 一、分析问题
// 已知:一棵树中的若干父节点和子节点的关系描述
// 未知:每个节点子节点的数量
// 关系:数组计数法
// 二、数据定义
int n, a[110] = {}, x, y; // n:节点总数;a[]:子节点计数数组;x, y:输入的父节点与子节点关系
// 三、数据输入
cin >> n; // 输入节点总数
// 读取并处理父节点与子节点关系
for (int i = 1; i < n; i++) {
cin >> x >> y; // 输入关系:节点x是节点y的父节点
a[x]++; // 更新数组a:节点x的子节点计数加1
}
// 四、数据计算与输出
// 直接输出数组a中的子节点计数,即每个节点的子节点数量
for (int i = 1; i <= n; i++) {
cout << a[i] << " "; // 输出节点i的子节点数量,后跟一个空格
}
// 五、输出结果
return 0; // 程序执行完毕,返回值为0
}
“哼~,真是一个有趣的题。”

问题二:2165 - 子结点的数量(2)
类型:树
题目描述:
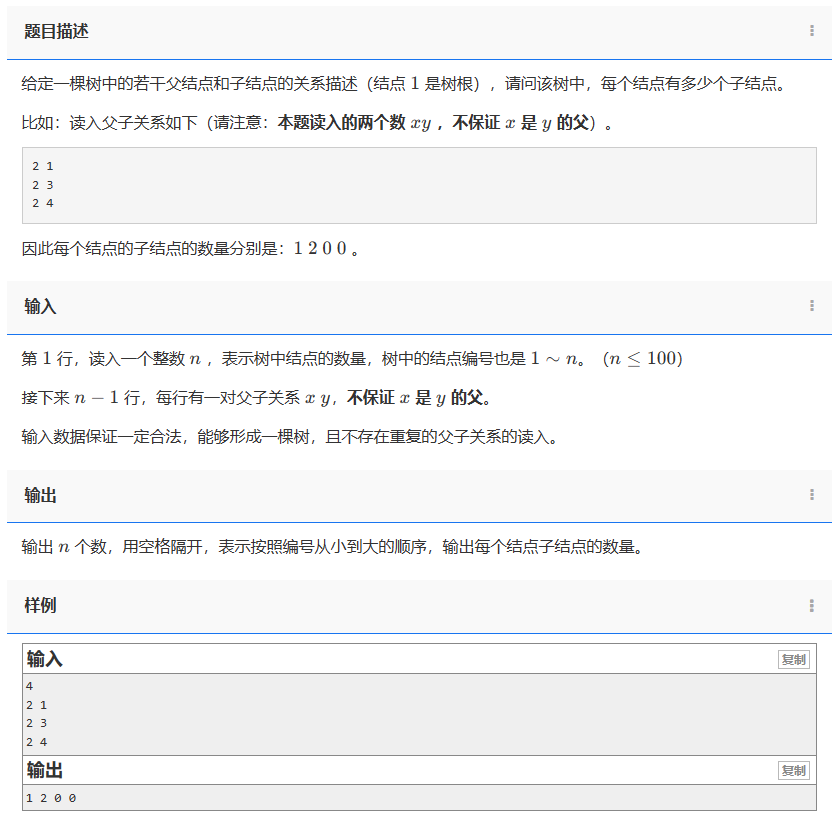
给定一棵树中的若干父结点和子结点的关系描述(结点 1 是树根),请问该树中,每个结点有多少个子结点。
比如:读入父子关系如下(请注意:本题读入的两个数 xy ,不保证 x 是 y 的父)。
1 2
2 3
2 4
因此每个结点的子结点的数量分别是:1 2 0 0 。
输入:
第 1 行,读入一个整数 n ,表示树中结点的数量,树中的结点编号也是1∼n。(n≤100)
接下来n−1 行,每行有一对父子关系 x y,不保证 x 是 y 的父。
输入数据保证一定合法,能够形成一棵树,且不存在重复的父子关系的读入。
输出:
输出 n 个数,用空格隔开,表示按照编号从小到大的顺序,输出每个结点子结点的数量。
样例:
输入:
4
2 1
2 3
2 4
输出:
1 2 0 0
解题思路:
首先这道题和上道题的解题方法是差不多。
不过差别在是什么地方呢?就是输入的数据。

题目这里明确表示了不保证x是y的父,那么就不能用上面所说的当了几次父亲那么就有几个儿子的统计办法。
还是利用样例进行分析。
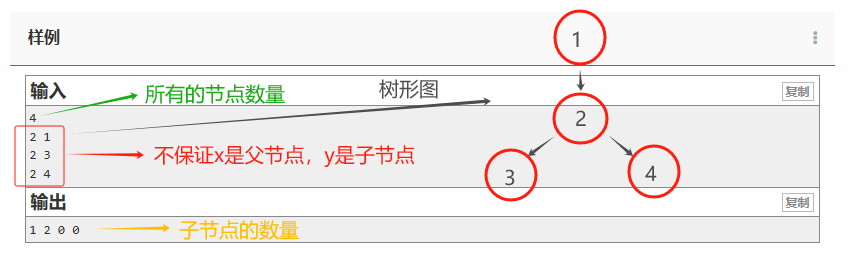
既然不能利用父节点来统计,那我们将目光移动到箭头。
还记得树的边吗?树的边是连接两个节点的连线,表示这两个节点之间存在某种关系或连接。
样例中2-1,2-3,2-4,那么我们就可以知道节点2拥有3条边,节点1,3,4有1条边。
而一个节点除了有子节点以外还有1个父节点,因此总边数-父节点那条边=子节点的边;那么有几条连接子节点的边就有几个子节点。
还是利用数组计数法,数组下标对应树的节点,每个节点每出现一次,表示该节点有一条边。
这里有一个点需要特别注意,根节点是没有父节点,因此要么对数组[1]进行额外的处理,要么将数组[1]多增加1,然后将数组[1-n]-1输出。
1.分析问题
- 已知:一棵树中的若干父节点和子节点的关系描述 (x不一定是y的父)。
- 未知:每个节点子节点的数量 。
- 关系:数组计数法,子节点数=边数-1(父节点)。
2.定义变量
// 二、数据定义
int a[110] = {}; // 初始化数组a,用于记录每个节点作为边端点的次数(视为子节点的次数)
int n, x, y; // n:节点总数;x, y:输入的节点对
3.输入数据
// 三、数据输入
cin >> n; // 读取节点总数
// 读取并处理节点对 (x, y),表示存在一条从节点x到节点y的边
for (int i = 1; i < n; i++) {
cin >> x >> y;
a[x]++; // 节点x参与了一条边,计数加1
a[y]++; // 节点y参与了一条边,计数加1
}
4.数据计算
// 四、数据计算
// 对根节点(结点1)特殊处理,手动增加其作为边端点的次数1,因为根节点没有父节点
a[1]++;
// 输出每个节点作为边端点的次数减1,即子节点数量(按题目特殊定义)
for (int i = 1; i <= n; i++) {
cout << a[i] - 1 << " "; // 输出节点i的子节点数量(按题目定义),后跟一个空格
}
5.输出结果
完整代码如下:
#include <iostream>
using namespace std;
int main() {
// 一、分析问题
// 已知:一棵树中的若干父节点和子节点的关系描述 (x不一定是y的父)。
// 未知:每个节点子节点的数量 。
// 关系:数组计数法,子节点数=边数-1(父节点)。
// 二、数据定义
int a[110] = {}; // 初始化数组a,用于记录每个节点作为边端点的次数(视为子节点的次数)
int n, x, y; // n:节点总数;x, y:输入的节点对
// 三、数据输入
cin >> n; // 读取节点总数
// 读取并处理节点对 (x, y),表示存在一条从节点x到节点y的边
for (int i = 1; i < n; i++) {
cin >> x >> y;
a[x]++; // 节点x参与了一条边,计数加1
a[y]++; // 节点y参与了一条边,计数加1
}
// 四、数据计算
// 对根节点(结点1)特殊处理,手动增加其作为边端点的次数1,因为根节点没有父节点
a[1]++;
// 输出每个节点作为边端点的次数减1,即子节点数量(按题目特殊定义)
for (int i = 1; i <= n; i++) {
cout << a[i] - 1 << " "; // 输出节点i的子节点数量(按题目定义),后跟一个空格
}
// 五、输出结果
return 0; // 程序执行完毕,返回值为0
}
问题三:1775 - 谁的孙子最多
类型:vector 树
题目描述:
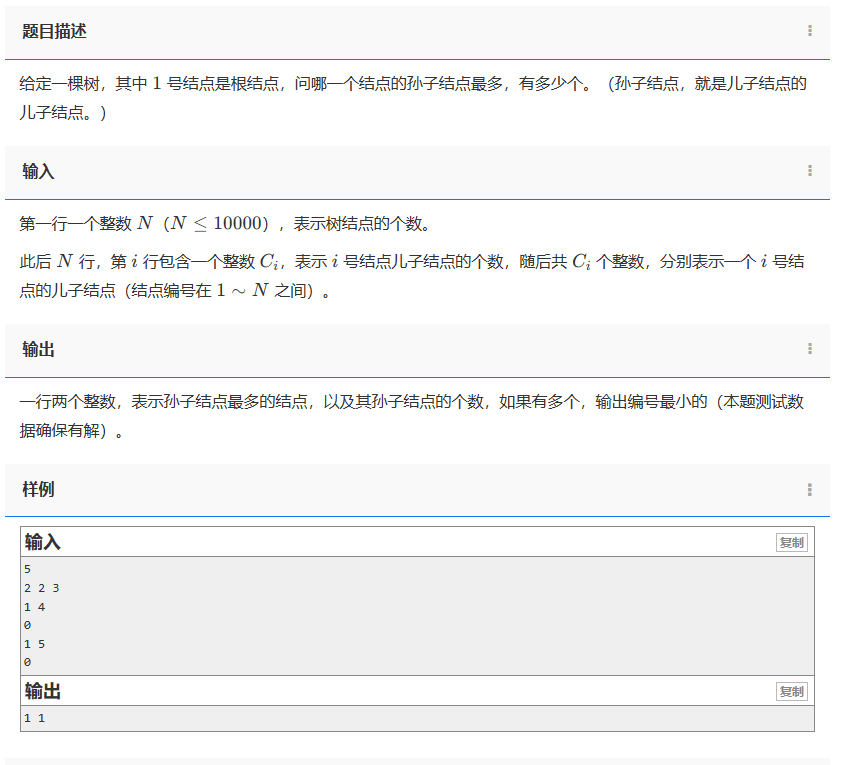
给定一棵树,其中 1 号结点是根结点,问哪一个结点的孙子结点最多,有多少个。(孙子结点,就是儿子结点的儿子结点。)
输入:
第一行一个整数 N(N≤10000),表示树结点的个数。
此后 N 行,第 i 行包含一个整数Ci,表示 i 号结点儿子结点的个数,随后共 Ci 个整数,分别表示一个 i 号结点的儿子结点(结点编号在1∼N 之间)。
输出:
一行两个整数,表示孙子结点最多的结点,以及其孙子结点的个数,如果有多个,输出编号最小的(本题测试数据确保有解)。
样例:
输入:
5
2 2 3
1 4
0
1 5
0
输出:
1 1
解题思路:
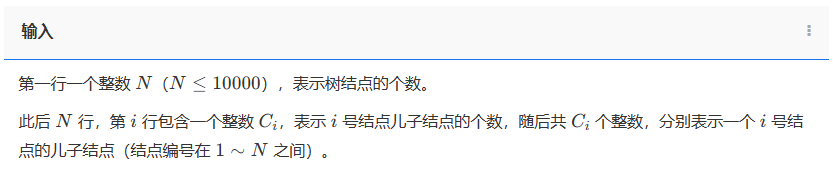
解题最重要的是读题。题目描述似乎没有太多有用的信息。因此我们将视线转移到输入中。
-
首先会输入一个整数n,n表示树结点的个数。
-
然后会输入n行数据,那么就需要用循环读入。每一行最少有一个整数c,c表示子结点的个数。如果c不等于0,那么还会有c个子结点被输入。因此需要考虑嵌套循环。
输入分析完成,看向输出。

- 输出只有一行,需要输出两个内容。内容1:孙子结点最多的结点,内容2:该结点的孙子结点数量。
- 要求如果存在有多个孙子结点数量相同的结点,优先输出编号小的。例如根结点1有3个孙子结点,结点2也有3个孙子结点,那么输出1不输出2。
分析完输入、输出后似乎还是没有完全读懂该题目。那只能从样例入手了。
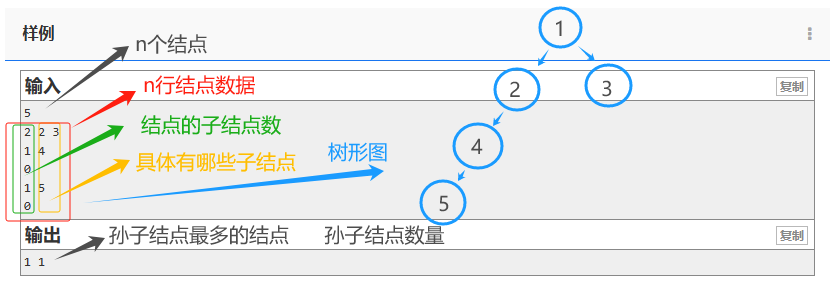
将样例中的信息标记出来,并画出树形图。
先不考虑本题如何求解,这些数据应该如何存储呢?
- 首先我们考虑孩子表示法,孩子表示法直接记录了每个节点的所有子节点编号,清晰地展现了树的父子关系,便于理解和操作。对于查找某个节点的所有后代、统计子树大小、遍历子树等与子节点相关操作,孩子表示法提供了直接的访问途径,无需额外计算或遍历。
- 其次vector允许在运行时动态添加或删除元素,无需预先知道树的具体形态。在输入节点及其子节点信息时,可以直接使用push_back()方法将子节点编号添加到父节点对应的vector中,无需手动管理内存。vector支持通过索引来直接访问和修改元素,对于孩子表示法中的子节点列表,可以通过a[i][j]快速访问第i个节点的第j个子节点,便于进行各种基于子节点的操作。
解决了该题的存储问题如何找到孙子的数量呢?
其实这个问题已经在不知不觉中被解决了。
使用了孩子表示法来存储树结构,每个节点的子节点编号被存储在一个vector中。vector的size()方法返回该向量中元素的数量,即当前节点的子节点数。
要计算某个节点i的孙子数量,实际上是计算其所有子节点的子节点数量之和。由于您已经将每个节点的子节点信息存储在其对应的vector中,即a[i],所以可以直接通过遍历a[i]中的每一个子节点z,然后调用a[z].size()来获取子节点z的子节点数量。将所有这些子节点数量累加,即可得到节点i的孙子数量。
1.分析问题
- 已知:
- 给定一棵树,其中1号结点为根结点。
- 树中节点总数N,满足N ≤ 10000。
- 对于每个节点i(1 ≤ i ≤ N):
已知其儿子结点数量C_i。
已知C_i个儿子结点的具体编号,均为1到N之间的整数。
- 未知:
- 哪一个结点的孙子结点数量最多。
- 这个结点的孙子结点数量是多少。
- 关系:
- 从已知信息出发,通过遍历树结构并统计每个节点的孙子结点数量。
- 对于每个节点i,其孙子结点数量等于其所有儿子结点的子节点数量之和。
- 通过比较所有节点的孙子结点数量,找出孙子结点数量最多的节点及其孙子结点数量。
- 若存在多个孙子结点数量最多的节点,选择编号最小的一个作为输出结果。
2.定义变量
声明变量 n(总节点数)、c(当前节点的儿子数)、x(儿子节点编号)、jd(孙子结点最多的节点编号)、jds(最大孙子结点数,初始值为INT_MIN)。
// 定义变量
int n, c, x, jd, jds = INT_MIN;
3.输入数据
读取总节点数 n,然后使用循环读取每个节点的子节点信息,将其存入二维向量 a 中。
// 读取总节点数
cin >> n;
// 依次读取每个节点的子节点信息,并存入一维数组a中
for (int i = 1; i <= n; i++) {
// 读取当前节点的儿子数
cin >> c;
// 读取并存储当前节点的每个儿子节点编号
for (int j = 0; j < c; j++) {
cin >> x;
a[i].push_back(x);
}
}
4.数据计算
遍历所有节点(编号从1到n),对于每个节点,计算其所有儿子节点的孙子结点总数(即儿子节点的子节点数量之和),如果当前节点的孙子结点总数大于之前找到的最大值,更新 jd 和 jds。
// 计算
// 遍历所有节点,寻找孙子结点最多的节点及其孙子结点数量
for (int i = 1; i <= n; i++) {
int sum = 0;
// 对于当前节点的每个儿子节点,累加其子节点数量(即孙子结点数量)
for (int j = 0; j < a[i].size(); j++) {
int ind = a[i][j];
sum += a[ind].size();
}
// 如果当前节点的孙子结点总数大于已知最大值,更新结果
if (sum > jds) {
jd = i;
jds = sum;
}
}
5.输出结果
最后输出孙子结点最多的节点编号 jd 以及对应的孙子结点数 jds。
// 输出
// 输出孙子结点最多的节点编号及其孙子结点数量
cout << jd << " " << jds;
完整代码如下:
#include <bits/stdc++.h>
using namespace std;
// 定义一个大小为100100的一维数组,每个元素为一个vector<int>,
// 用于存储每个节点的子节点编号
vector<int> a[100100];
int main() {
// 定义变量
int n, c, x, jd, jds = INT_MIN;
// 输入
// 读取总节点数
cin >> n;
// 依次读取每个节点的子节点信息,并存入一维数组a中
for (int i = 1; i <= n; i++) {
// 读取当前节点的儿子数
cin >> c;
// 读取并存储当前节点的每个儿子节点编号
for (int j = 0; j < c; j++) {
cin >> x;
a[i].push_back(x);
}
}
// 计算
// 遍历所有节点,寻找孙子结点最多的节点及其孙子结点数量
for (int i = 1; i <= n; i++) {
int sum = 0;
// 对于当前节点的每个儿子节点,累加其子节点数量(即孙子结点数量)
for (int j = 0; j < a[i].size(); j++) {
int ind = a[i][j];
sum += a[ind].size();
}
// 如果当前节点的孙子结点总数大于已知最大值,更新结果
if (sum > jds) {
jd = i;
jds = sum;
}
}
// 输出
// 输出孙子结点最多的节点编号及其孙子结点数量
cout << jd << " " << jds;
return 0;
}
问题四:1776 - 谁的孙子最多II
类型:vector 树
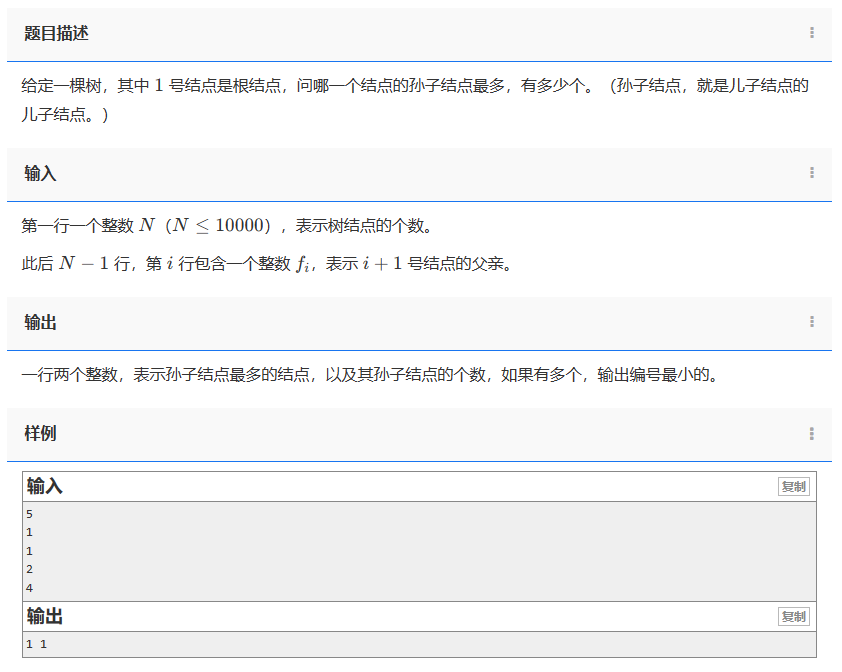
题目描述:
给定一棵树,其中 1 号结点是根结点,问哪一个结点的孙子结点最多,有多少个。(孙子结点,就是儿子结点的儿子结点。)
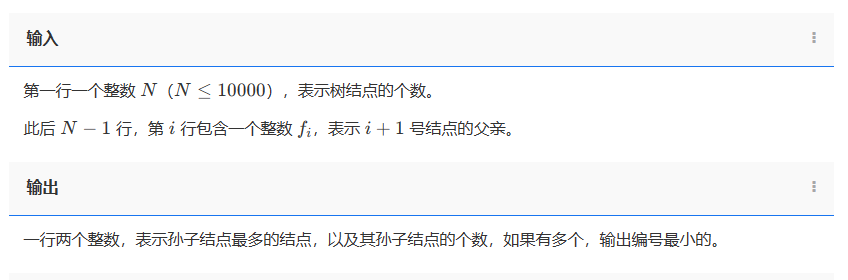
输入:
第一行一个整数 N(N≤10000),表示树结点的个数。
此后N−1 行,第 i 行包含一个整数fi,表示 i+1 号结点的父亲。
输出:
一行两个整数,表示孙子结点最多的结点,以及其孙子结点的个数,如果有多个,输出编号最小的。
样例:
输入:
5
1
1
2
4
输出:
1 1
解题思路:
本题和《1775 - 谁的孙子最多》这题的内容相似,都是要找谁的孙子结点最多,那具体有什么不同呢?我们进一步研究。
还是从输入、输出入手。
首先输出很简单,就是要输出孙子结点最多的结点,和它的个数。定义出相关的变量即可。
输入:
- 首先输入一个整数n,表示结点总数。
int n;
cin>>n;
- 剩下n-1行,每行会输入n+1结点的父亲。
for(int i=1;i<n;i++)
老规矩,还是分析样例。
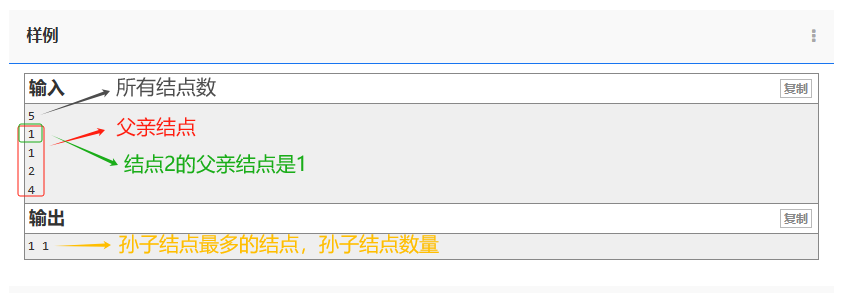
分析完样例后,似乎可以使用vector-父亲表示法,但是我们本题是要寻找孙子数量最多,而父亲表示法适用于需要频繁向上追溯父节点的场景,但不利于进行自底向上的遍历。
所以我们本题还是转换成孩子表示法。
如何转换?
其实当我们说一个结点是一个结点的父亲时,也可以说这个结点是另外一个结点的孩子。比如说a结点是b结点的父亲,那么我们说b结点是a结点的孩子。
样例中第二个结点的父亲是1结点,也可以说1结点的孩子是2结点。
将循环的i作为孩子,将输入的f作为父亲。
for(int i=2;i<n;i++){
cin>>f;
a[f].push_back(i);
}
剩下的如何处理哪个结点的孙子结点最多就和《1775 - 谁的孙子最多》一样了。
1.分析问题
- 已知:一棵树,它的结点信息。
- 未知:哪个结点的孙子结点最多,数量是多少。
- 关系:孩子表示法,vector。
2.定义变量
// 定义变量
int n, f, jd, jds = INT_MIN;
3.输入数据
// 依次读取每个节点的父节点信息,并存入一维数组a中
for (int i = 2; i <=n; i++) {
// 读取当前节点的父结点
cin >> f;
//转换成父结点的子结点信息。
a[f].push_back(i);
}
4.数据计算
// 计算
// 遍历所有节点,寻找孙子结点最多的节点及其孙子结点数量
for (int i = 1; i <= n; i++) {
int sum = 0;
// 对于当前节点的每个儿子节点,累加其子节点数量(即孙子结点数量)
for (int j = 0; j < a[i].size(); j++) {
int ind = a[i][j];
sum += a[ind].size();
}
// 如果当前节点的孙子结点总数大于已知最大值,更新结果
if (sum > jds) {
jd = i;
jds = sum;
}
}
5.输出结果
// 输出
// 输出孙子结点最多的节点编号及其孙子结点数量
cout << jd << " " << jds;
完整代码如下:
#include <bits/stdc++.h>
using namespace std;
// 定义一个大小为100100的一维数组,每个元素为一个vector<int>,
// 用于存储每个节点的子节点编号
vector<int> a[100100];
int main() {
// 定义变量
int n, f, jd, jds = INT_MIN;
// 输入
// 读取总节点数
cin >> n;
// 依次读取每个节点的父节点信息,并存入一维数组a中
for (int i = 2; i <=n; i++) {
// 读取当前节点的父结点
cin >> f;
//转换成父结点的子结点信息。
a[f].push_back(i);
}
// 计算
// 遍历所有节点,寻找孙子结点最多的节点及其孙子结点数量
for (int i = 1; i <= n; i++) {
int sum = 0;
// 对于当前节点的每个儿子节点,累加其子节点数量(即孙子结点数量)
for (int j = 0; j < a[i].size(); j++) {
int ind = a[i][j];
sum += a[ind].size();
}
// 如果当前节点的孙子结点总数大于已知最大值,更新结果
if (sum > jds) {
jd = i;
jds = sum;
}
}
// 输出
// 输出孙子结点最多的节点编号及其孙子结点数量
cout << jd << " " << jds;
return 0;
}