在计算几何中，判定点是否在多边形内，是个非常有趣的问题。通常有两种方法：

一、Crossing Number（交叉数）

它计算从点P开始的射线穿过多边形边界的次数。当“交叉数”是偶数时，点在外面;当它是奇数时，点在里面。这种方法有时被称为“奇-偶”检验。

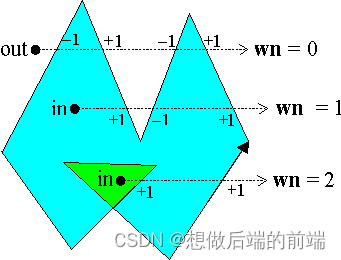
如果一个多边形是不自交的（称为“简单多边形”），那么这两种方法对任意点都给出相同的结果。但对于非简单多边形，这两种方法在某些情况下会给出不同的答案。如下图所示，当一个多边形与自身重叠时，对于重叠区域内的点，如果使用交叉数判断，它在外面；而使用环绕数判断则在里面。

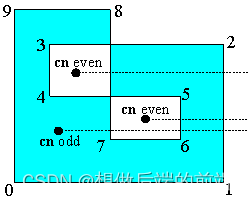
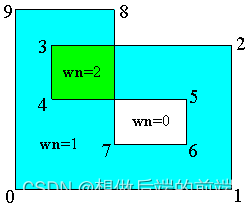
在上图中，绿色区域中的点，wn = 2，表示在多边形中重叠了2次。相比于Crossing number，winding number给出了更内蕴性的答案。

尽管如此，早些时候，crossing number方法应用的更广泛，因为最初计算几何专家们错误地认为crossing number比winding number计算起来更加高效。但事实并非如此，两者的时间复杂度完全一样。Franklin在2000年给出一个计算winding number的非常快的实现。因此，为了几何正确性和效率的原因，在确定一个多边形中的一个点时，wn算法应该总是首选的。

该方法计算从点P开始的射线穿过多边形边界的次数（不管穿过的方向）。如果这个数是偶数，那么点在外面;否则，当交叉数为奇数时，点在多边形内。其正确性很容易理解，因为每次射线穿过多边形边缘时，它的内外奇偶性都会发生变化(因为边界总是分隔内外)。最终，任何射线都在边界多边形之外结束。所以，如果点在多边形内，那么对边界的穿过次序一定是：out>…>in>out,因此交叉数一定是奇数；同样地，如果点在多边形外，那么对边界的穿过次序一定是in > out … > in > out,因此交叉数必是偶数。
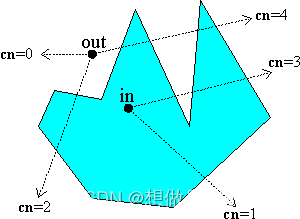在实现crossing number的算法时，必须确保只计算改变奇偶性的交叉位置。特别是，对于射线穿过顶点的情况需要适当的处理。下图列举了射线与多边形可能的相交情况：

此外，必须确定多边形边界上的点P是在内部还是外部。一般约定：如果点在边的左侧，那么认为点P在内部；如果点在边的右侧，那么认为点P在外部。如果两个不同的多边形共享一个共同的边界线段，那么该线段上的一点将会在一个多边形或另一个多边形中，而不是同时在两个多边形中。这避免了许多可能发生的问题，特别是在计算机图形显示中。

一个简单的做法是选择一条x轴正方向的水平射线，对于这样一条射线，很容易计算多边形的边与它的交点。而且，很容易确定交点是否存在。算法只需沿着多边形的每一条边，依次计算交点，当相交时，cn增加1，从而计算出最终的总交叉数。

此外，相交测试必须遵循如下的规则，处理一些特殊情况（如上图）：

• 向上的边，包含起点，但不包含终点；
• 向下的边，包含终点，但不包含起点；
• 水平的边，不包含起点和终点；
• 边与射线的交点必须严格在点P的右侧

按照上述规则，处理特殊的相交情况，就能得到正确的交叉数。其中，规则4将导致在边界右侧的点在多边形外部，在左侧的点将会被判定为在内部。

Crossing Number Pseudo-Code：
对于n个点组成的多边形V={V[0], V[1], …,V[n]},其中V[n]=V[0], 计算几何大牛Franklin给出了一个非常有名的实现：

typedef struct {int x, y;} Point;
 
cn_PnPoly( Point P, Point V[], int n )
{
    int    cn = 0;    // the  crossing number counter
 
    // loop through all edges of the polygon
    for (each edge E[i]:V[i]V[i+1] of the polygon) {
        if (E[i] crosses upward ala Rule #1
         || E[i] crosses downward ala  Rule #2) {
            if (P.x <  x_intersect of E[i] with y=P.y)   // Rule #4
                 ++cn;   // a valid crossing to the right of P.x
        }
    }
    return (cn&1);    // 0 if even (out), and 1 if  odd (in)
 
}

注意，对于满足规则1和2的向上和向下交叉的测试也排除了水平边缘(规则3)。总而言之，很多工作是通过几个测试完成的，这使得这个算法很优雅。

然而，交叉数方法的有效性是基于“约当曲线定理”（Jordan Curve Theorem），该定理表明，一条简单的闭合曲线将二维平面分成两个完全连通的分量:一个有界的“内”分量和一个无界的“外”分量。需要注意的是，曲线必须是简单的(没有自身交叉)，否则可能有两个以上的组成部分，然后就不能保证跨越边界改变进出奇偶性。因此，该方法不适用于自相交的多边形。

二、Winding Number（环绕数）

它计算多边形绕着点P旋转的次数。只有当“圈数”wn = 0时，点才在外面; 否则，点在里面。

winding number方法能准确判定一个点是否在自交的封闭曲线内。该方法通过计算多边形有多少次环绕点P来实现。只有当多边形不环绕该点，也就是环绕数wn = 0时，一个点才在外面。

不妨定义：平面上的点P相对于任意连续封闭曲线的环绕数为{wn}(P,C)。对于一条水平向右的射线R，我们每一条与R相交的边需要判断其终点在R上面还是下面。如果边从下往上穿过R，wn+1；否则wn-1。所有边遍历一遍，最终得到总的f{wn}(P,C)，如下图所示：

此外，我们没必要计算实际的交点，只需要使用如下方法判断当前穿过的边的环绕数应该+1还是-1：

如下图所示，如果一条边向上穿过射线R，那么P点在边ViVi+1的左侧；而对于一条向下的边，P点在边ViVi+1的右侧。

通过以上分析，容易给出如下的wn计算伪代码（和cn的计算一样使用相同的边相交规则）：

 
typedef struct {int x, y;} Point;
 
wn_PnPoly( Point P, Point V[], int n )
{
    int    wn = 0;    // the  winding number counter
 
    // loop through all edges of the polygon
    for (each edge E[i]:V[i]V[i+1] of the polygon) {
        if (E[i] crosses upward ala Rule #1)  {
            if (P is  strictly left of E[i])    // Rule #4
                 ++wn;   // a valid up intersect right of P.x
        }
        else
        if (E[i] crosses downward ala Rule  #2) {
            if (P is  strictly right of E[i])   // Rule #4
                 --wn;   // a valid down intersect right of P.x
        }
    }
    return wn;    // =0 <=> P is outside the polygon
 
}

显然，环绕数方法与交叉数方法有着相同的计算效率。但由于该方法更加具有普遍性，因此，在确定一个点是否在任意多边形内时，推荐使用Winding Number方法。

通过一些技巧可以进一步提高wn算法的效率，在下面给出的wn_PnPoly() 的实现中，我们可以看到这一点。在该代码中，所有完全在P以上或完全在P以下的边只经过两次不等式检验就被拒绝（没有交点）。然而，在目前流行的cn算法的实现中，需要3次不等式检验才能做到这一点。由于在实际应用中，大多数边都会被拒绝，因此进行比较的次数减少了大约33%(或更多)。在使用非常大的(1,000,000边)随机多边形(边长<多边形直径的1/10)和1000个随机测试点(在多边形的边界内)进行运行时测试时，测试结果表明wn算法的平均效率提高了20%。