目录
一,背景
二,华容道中道
1,问题
2,告诉脑机如何编码一个正方形格子
3,让脑机汇总信息
4,观察图,得到启发式算法
5,根据启发式算法求出具体解
6,可视化
一,背景
畅想一下脑机接口成熟之后,当我们遇到一个问题,可能会怎么样使用脑机去解决。
如果思路比较明确,且时间复杂度比较低,可以直接让脑机采用***算法解决问题。
如果有一些灵感,但是没有明确的思路,只有一个非P时间复杂度的垃圾算法,那就可以在脑机的辅助下,逐步推导出什么才是合适的算法。
PS:推导出的可能是比较适合当下情况的算法,而不是通用算法。
二,华容道中道
以最强大脑的《华容道中道》这个项目为例,来模拟一下如何逐步推导出什么才是合适的算法。
1,问题
把数字华容道的数字格变成迷宫格,拼出一条路径出来。
题面(选手比赛玩的就是这个):

2,告诉脑机如何编码一个正方形格子
我的指令:
对于每个正方形格子,边长为3,即由12个单位线段组成。
依次编号1-12,找到缺失的线段,一般都是2个缺口,把2个缺口id记为pair(a,b),1<=a<b<=12
脑机回复:
是这样吗?

我的回复:
是的
3,让脑机汇总信息
我的指令:
统计某个格子,如果有哪个格子的缺口数不是2,单独报告给我。
对于缺口数是2的,按照迷宫规则,判定这2个缺口是否连通,如果不连通,单独报告给我。
对于连通的格子,汇总所有的pair结果
脑机回复:
没有缺口数不是2的,也没有不连通的。99个格子的编码依次是:
5 6 5 8 9 10 6 8 5 8 5 8 7 8 5 6 2 3 7 10
6 7 6 7 5 9 6 8 4 5 1 9 5 7 3 8 10 11 6 9
8 9 9 12 3 4 2 12 5 9 1 8 10 11 1 10 6 8 3 8
1 11 2 5 8 12 4 8 2 10 3 8 3 4 7 10 4 11 4 5
5 8 4 8 2 11 6 11 1 10 3 5 6 9 3 11 11 12 3 4
2 4 6 12 8 10 7 10 5 11 3 5 1 10 1 12 3 11 2 10
8 12 4 11 2 11 4 11 7 12 3 4 9 11 9 11 6 7 2 5
2 6 5 8 4 11 4 7 2 6 9 11 5 11 4 10 4 10 10 11
6 10 5 10 3 11 2 8 5 7 6 12 9 10 3 9 1 10 10 11
7 8 1 11 2 11 6 7 8 10 7 8 5 10 6 8 1 2
我的指令:
计数汇总
脑机回复:
1 10 4
1 11 2
1 12 1
1 2 1
1 8 1
1 9 1
10 11 4
11 12 1
2 10 2
2 11 3
2 12 1
2 3 1
2 4 1
2 5 2
2 6 2
2 8 1
3 11 3
3 4 4
3 5 2
3 8 3
3 9 1
4 10 2
4 11 4
4 5 2
4 7 1
4 8 2
5 10 2
5 11 2
5 6 2
5 7 2
5 8 5
5 9 2
6 10 1
6 11 1
6 12 2
6 7 4
6 8 4
6 9 2
7 10 3
7 12 1
7 8 3
8 10 2
8 12 2
8 9 1
9 10 2
9 11 3
9 12 1
我的指令:
画个图
脑机回复:
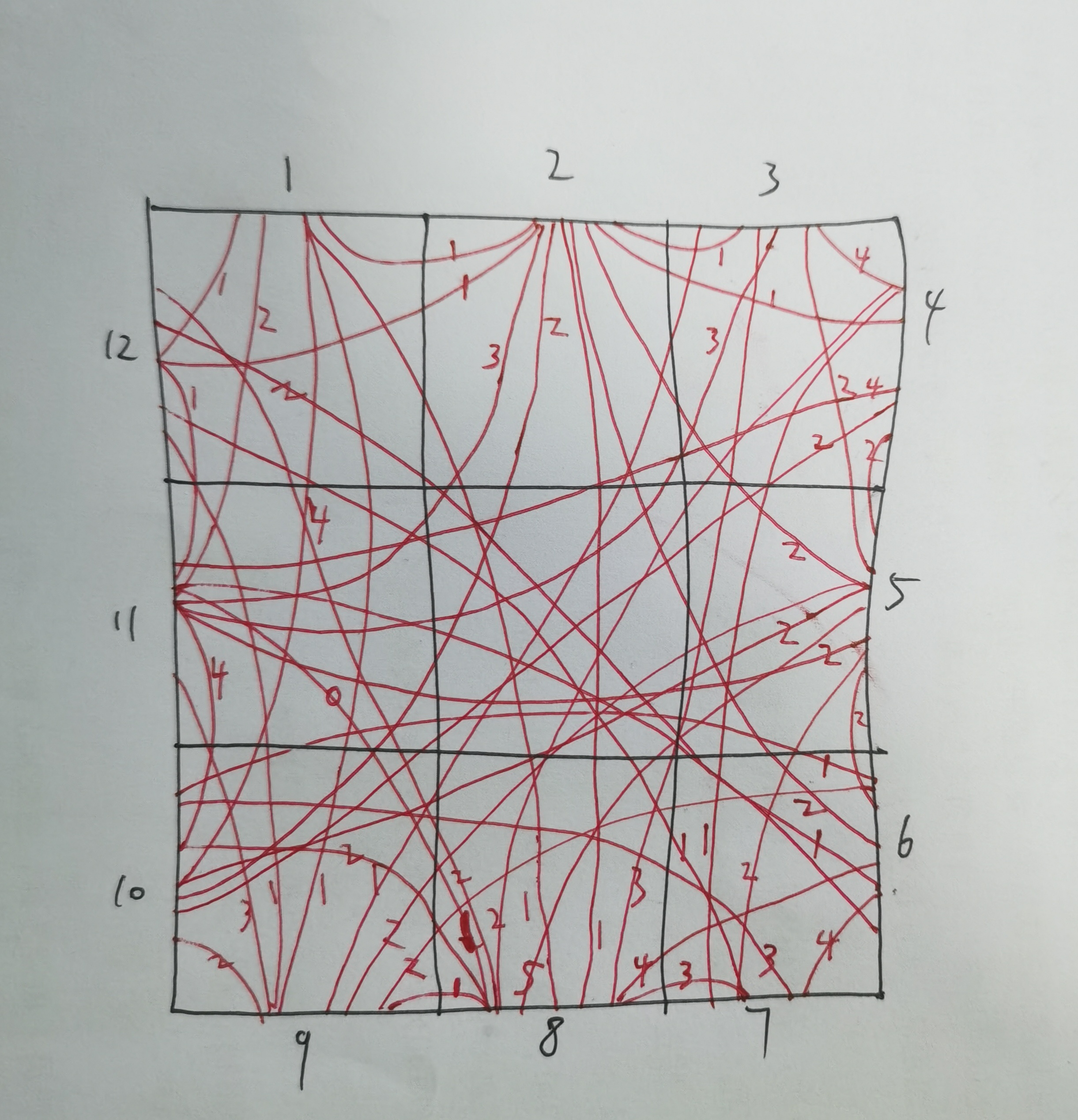
PS:图文稍微有一点点不对应,以文字为准。
4,观察图,得到启发式算法
目前看来,应该存在理论最短路(由18个格子组成的迷宫线路),或者接近最短路(不超过20个)。
我们可以先试试,能不能找到理论最短路。
我的指令:
把一端在左边或上边,一端在右边或下边的线给挑选出来,汇总结果。
脑机回复:
1 8 1
1 9 1
2 4 1
2 5 2
2 6 2
2 8 1
3 4 4
3 5 2
3 8 3
3 9 1
4 10 2
4 11 4
5 10 2
5 11 2
6 10 1
6 11 1
6 12 2
7 10 3
7 12 1
8 10 2
8 12 2
9 10 2
9 11 3
9 12 1
脑机回复:
1 下 2
2 右 5
2 下 1
3 右 6
3 下 4
10 右 5
10 下 7
11 右 7
11 下 3
12 右 2
12 下 4
我的回复:
好的,我已经找到了特征,简单来说,1的出口比较少,其次是2的下边出口比较少,3,10,11,12的出口比较多。
于是我们得到了启发式算法:
直接按照数量挑路径,尽量往右穿边界和往下穿边界交替进行,控制往9走的次数,因为9连着1
5,根据启发式算法求出具体解
我的指令:
把“一端在左边或上边,一端在右边或下边的线”对应的子图再画出来。
脑机回复:
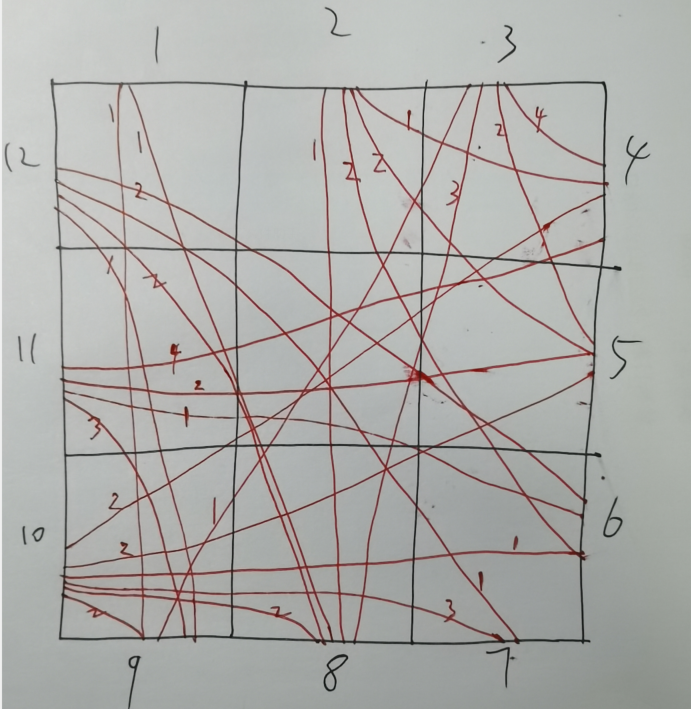
我的回复:
基于这个图,我直接很容易算出答案:
12 7
3 8
2 5
11 9
1 9
1 8
2 4
12 8
2 6
10 6
10 4
12 8
2 5
11 6
10 8
2 8
2 6
10 7
6,可视化
我的指令:
帮我把上面这个答案,对应的格子标出来
脑机回复: