0. 分类分析概述

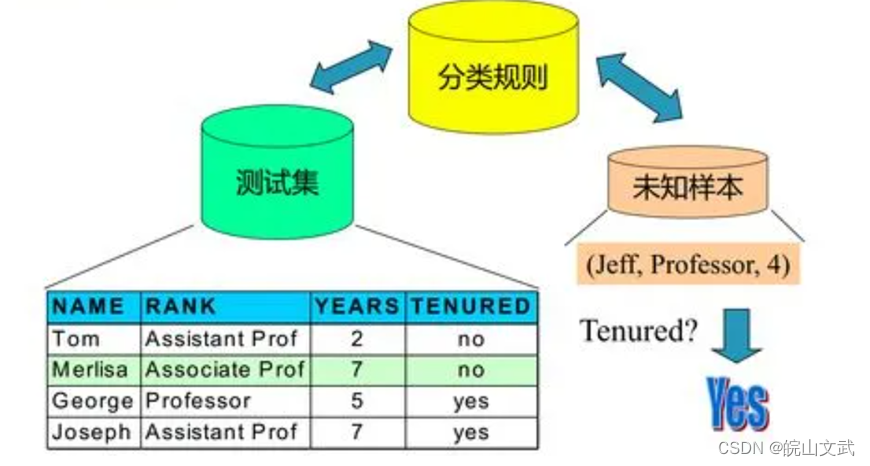
分类是数据挖掘的主要方法，通过有指导的学习训练建立分类模型。

分类的目的是通过学习，得到一个分类函数或分类模型（也常常称作分类器），该模型能够把数据集中的对象映射到给定类别中的某一个类上。
分类和回归都属于预测建模，分类用于预测可分类属性或变量，而回归用于预测连续的属性取值。

1. Logistics回归模型

最常见的分类预测模型为：

$$log(\frac{P}{1-P})={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+...+{\beta }_p{X}_p+\epsilon$$
该模型被称为Logistics回归模型，适用于输出变量仅有0、1两个类别（或分类）值的二分类预测。例如：基于顾客的购买行为预测其是否会参加本次对该类商品的促销。

2. 贝叶斯分类器

在实际应用中，样本的属性集与类别的关系一般是不确定的，但可能存在一种概率关系。贝叶斯分类器是一种基于统计概率的分类器，通过比较样本术语不同类别的概率大小对其进行分类。
这里对朴素贝叶斯分类器进行介绍，朴素贝叶斯分类器是贝叶斯定理（一种样本属性集与类别的概率关系建模方法）的实现。

2.1 贝叶斯定理

假设$X$和$Y$在分类中可以分别表示样本的属性集和类别。$p(X,Y)$表示它们的联合概率，$p(X|Y)$和$p(Y|X)$表示条件概率，其中$p(Y|X)$是后验概率，而$p(Y)$称为$Y$的先验概率。$X$和$Y$的联合概率和条件概率满足下列关系：
$$p(X,Y)=p(Y|X)p(X)=p(X|Y)p(Y)$$
变换后得到：
$$p(Y|X)=\frac{p(X|Y)p(Y)}{p(X)}$$
上式称为贝叶斯定理，它提供了从先验概率$p(Y)$计算后验概率$p(Y|X)$的方法。
在分类时，给定测试样本的属性集$X$，利用训练样本数据可以计算不同类别$Y$值的后验概率，后验概率$p(Y|X)$最大的类别$Y$可以作为样本的分类。

2.2 朴素贝叶斯分类器

在应用贝叶斯定理时，$p(X|Y)$的计算比较麻烦。但对于属性集$X=X_1,X_2,...,X_n$，如果$X_1,X_2,...,X_n$之间互相独立，即$p(X|Y)=\prod _{i=1}^{n}p(X_i|Y)$，这个问题就可以由朴素贝叶斯分类器来解决：
$$p(Y|X)=\frac{p(Y)\prod _{i=1}^{n}p(X_i|Y)}{p(X)}$$
其中$p(X)$是常数，先验概率$p(Y)$可以通过训练集中每类样本所占的比例估计。给定$Y=y$，如果要估计测试样本$X$的分类，由朴素贝叶斯分类器得到$y$类的后验概率：
$$p(Y=y|X)=\frac{p(Y=y)\prod _{i=1}^{n}p(X_i|Y=y)}{p(X)}$$
只要找出使$p(Y=y)\prod _{i=1}^{n}p(X_i|Y=y)$最大的类别$y$即可。
朴素贝叶斯分类器简单高效，常用于入侵检测或文本分类等领域。这种分类模型能较好地处理训练样本的噪声和无关属性，减少对数据的过度拟合。
朴素贝叶斯分类器要求严格的条件独立性假设，但现实属性之间一般都有一定的相关性，因此对于实际应用中某些属性有一定相关性的分类问题，效果往往并不理想。

2.2.1 高斯朴素贝叶斯分类器

在估算条件概率$P(x_i|c)$时，如果$x_i$为连续值，可以使用高斯朴素贝叶斯（Gaussian Naive Bayes）分类模型，它基于一种经典的假设：与每个类相关的连续变量的分布是属于高斯分布的。

2.2.2 多项式朴素贝叶斯分类器

多项式朴素贝叶斯（Multinomial Naive Bayes）经常被用于离散特征的多分类问题，比原始的朴素贝叶斯分类效果有了较大提升。

2.3 朴素贝叶斯分类的主要优点

(1) 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
(2) 对小规模的数据集表现很好，可以处理多分类任务。适合增量式训练，尤其是数据量超出内存时，可以一批批的去增量训练。
(3) 对缺失数据不太敏感，算法也比较简单，常用于文本分类。

2.4 朴素贝叶斯分类的主要缺点

(1) 理论上，朴素贝叶斯模型与其它分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。
(2) 需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型原因导致预测效果不佳。
(3) 由于我们是通过先验概率来决定后验概率从而决定分类，所以分类决策存在一定的错误率。
(4) 对输入数据的表达形式很敏感。

3. 贝叶斯分类器在生产中的应用

供电电容是计算机主板生产商必备的工业组件,质量好的供电电容可以提高主板的供电效率,所以供电电容的质量也就直接决定了主板的使用寿命。假设某段时期内某计算机主板制造商所用的供电电容是由三家电容生产商提供的。对制造商在这段时期内的业务数据进行抽样,得到下表所示数据。

生产商标识	次品率	提供电容的份额
1	2%	15%
2	1%	80%
3	3%	5%

三家电容工厂的供电电容在电脑主板生产商的仓库中是均匀混合的,并无明显的区别标志。现在电脑主板生产商想通过对数据进行分析,解决下面两个问题：

(1) 随机地从仓库中取一只供电电容是次品的概率。
(2)从仓库中随机地取一只供电电容,若已知取到的是一只次品,那么此次品来自哪家工厂的可能性最大。

假设$X$表示“取到的是一只次品”，$Y=i(i=1,2,3)$表示“取到的产品是由第$i$家工厂提供的”，则问题转化为求解$p(X)$与$p(Y=i|X)$。由上表得到后验概率为：

$$p(X|Y=1)=2\%,p(X|Y=2)=1\%,p(X|Y=3)=3\%$$
先验概率为：
$$p(Y=1)=15\%,p(Y=2)=80\%,p(Y=3)=5\%$$
由全概率公式计算得出：
$$\begin{gathered} p(X)=p(X|Y=1)p(Y=1)+p(X|Y=2)p(Y=2)+p(X|Y=3)p(Y=3) \\ =0.02\ast 0.15+0.01\ast 0.8+0.03\ast 0.05=0.0125 \end{gathered}$$
然后求解$p(Y=i|X)$，根据贝叶斯定理可得：
$$p(Y=i|X)=\frac{p(X|Y=i)p(Y=i)}{p(X)}$$
由上式可以计算次品出自厂商1的概率为：
$$p(Y=1|X)=\frac{p(X|Y=1)p(Y=1)}{p(X)}=\frac{0.02\ast 0.15}{0.0125}=0.24$$
类似地可以计算次品出自其他两个厂商的概率为：
$$p(Y=2|X)=0.64，p(Y=3|X)=0.12$$
可见，从仓库中随机地取一只电容，如果是一只次品，那么此次品来自工厂2的可能性最大。

4. 朴素贝叶斯分类器的Python实现

利用scikit-learn中朴素贝叶斯的分类算法

from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB
iris = load_iris()
clf = GaussianNB()# 设置高斯贝叶斯分类器
clf.fit(iris.data,iris.target)# 训练分类器
y_pred = clf.predict(iris.data)# 预测
print("Number of mislabeled points out of %d points:%d" %(iris.data.shape[0],(iris.target!= y_pred).sum()))

Number of mislabeled points out of 150 points:6

from sklearn.datasets import load_iris
from sklearn.naive_bayes import MultinomialNB
iris = load_iris()
gnb =MultinomialNB()# 设置多项式贝叶斯分类器
gnb.fit(iris.data,iris.target)
y_pred=gnb.predict(iris.data)
print('Number of mislabeled points out of a total  %d points: %d' %(iris.data.shape[0],(iris.target!= y_pred).sum()))

Number of mislabeled points out of a total  150 points: 7

5. 贝叶斯分类器和Logistic回归分类边界的对比

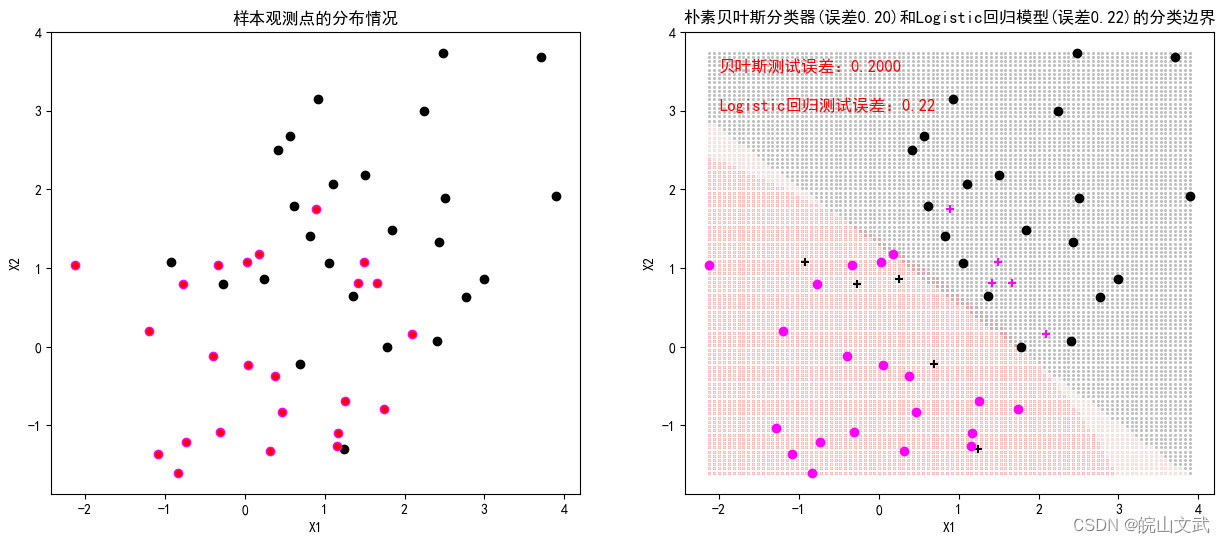
基于模拟数据分别建立朴素贝叶斯分类器和Logistic回归模型，并绘制两个分类模型的分类边界，展示两者的特点和区别。
代码及运行结果如下：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
import warnings
warnings.filterwarnings(action = 'ignore')
from scipy.stats import beta
from sklearn.naive_bayes import GaussianNB
import sklearn.linear_model as LM
from sklearn.model_selection import cross_val_score,cross_validate,train_test_split
from sklearn.metrics import classification_report
from sklearn.metrics import roc_curve, auc,accuracy_score,precision_recall_curve
np.random.seed(123)
N=50
n=int(0.5*N)
X=np.random.normal(0,1,size=100).reshape(N,2)
Y=[0]*n+[1]*n
X[0:n]=X[0:n]+1.5

fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(15,6))
axes[0].scatter(X[:n,0],X[:n,1],color='black',marker='o')
axes[0].scatter(X[(n+1):N,0],X[(n+1):N,1],edgecolors='magenta',marker='o',c='r')
axes[0].set_title("样本观测点的分布情况")
axes[0].set_xlabel("X1")
axes[0].set_ylabel("X2")

modelNB = GaussianNB()
modelNB.fit(X, Y)
modelLR=LM.LogisticRegression()
modelLR.fit(X,Y)
Data=np.hstack((X,np.array(Y).reshape(N,1)))
Yhat=modelNB.predict(X)
Data=np.hstack((Data,Yhat.reshape(N,1)))
Data=pd.DataFrame(Data)

X1,X2 = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),100), np.linspace(X[:,1].min(),X[:,1].max(),100))
New=np.hstack((X1.reshape(10000,1),X2.reshape(10000,1)))
YnewHat1=modelNB.predict(New)
DataNew=np.hstack((New,YnewHat1.reshape(10000,1)))
YnewHat2=modelLR.predict(New)
DataNew=np.hstack((DataNew,YnewHat2.reshape(10000,1)))
DataNew=pd.DataFrame(DataNew)

for k,c in [(0,'silver'),(1,'red')]:
    axes[1].scatter(DataNew.loc[DataNew[2]==k,0],DataNew.loc[DataNew[2]==k,1],color=c,marker='o',s=1)
for k,c in [(0,'silver'),(1,'mistyrose')]:
    axes[1].scatter(DataNew.loc[DataNew[3]==k,0],DataNew.loc[DataNew[3]==k,1],color=c,marker='o',s=1)

axes[1].scatter(X[:n,0],X[:n,1],color='black',marker='+')
axes[1].scatter(X[(n+1):N,0],X[(n+1):N,1],color='magenta',marker='+')
for k,c in [(0,'black'),(1,'magenta')]:
    axes[1].scatter(Data.loc[(Data[2]==k) & (Data[3]==k),0],Data.loc[(Data[2]==k) & (Data[3]==k),1],color=c,marker='o')
axes[1].set_title("朴素贝叶斯分类器(误差%.2f)和Logistic回归模型(误差%.2f)的分类边界"%(1-modelNB.score(X,Y),1-modelLR.score(X,Y)))
axes[1].set_xlabel("X1")
axes[1].set_ylabel("X2")

np.random.seed(123)
k=10
CVscore=cross_validate(modelNB,X,Y,cv=k,scoring='accuracy',return_train_score=True) 
axes[1].text(-2,3.5,'贝叶斯测试误差：%.4f' %(1-CVscore['test_score'].mean()),fontsize=12,color='r')
CVscore=cross_validate(modelLR,X,Y,cv=k,scoring='accuracy',return_train_score=True) 
axes[1].text(-2,3,"Logistic回归测试误差：%.2f" %(1-CVscore['test_score'].mean()),fontsize=12,color='r')
plt.show()

6. 空气污染的分类预测

基于空气质量监测数据，采用朴素贝叶斯分类器对是否出现空气污染进行二分类预测，然后采用各种方式对预测模型进行评价。
代码及运行结果如下：

data=pd.read_excel('北京市空气质量数据.xlsx')
data=data.replace(0,np.NaN)
data=data.dropna()
data['有无污染']=data['质量等级'].map({'优':0,'良':0,'轻度污染':1,'中度污染':1,'重度污染':1,'严重污染':1})
data['有无污染'].value_counts()
X=data.loc[:,['PM2.5','PM10','SO2','CO','NO2','O3']]
Y=data.loc[:,'有无污染']

modelNB = GaussianNB()
modelNB.fit(X, Y)
modelLR=LM.LogisticRegression()
modelLR.fit(X,Y)
print('评价模型结果：\n',classification_report(Y,modelNB.predict(X)))

评价模型结果：
               precision    recall  f1-score   support

           0       0.86      0.94      0.90      1204
           1       0.90      0.79      0.84       892

    accuracy                           0.88      2096
   macro avg       0.88      0.87      0.87      2096
weighted avg       0.88      0.88      0.87      2096

接下来，利用ROC和P-R曲线对比朴素贝叶斯分类器和Logistic回归模型的预测性能。
代码及运行结果如下：

fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4))
fpr,tpr,thresholds = roc_curve(Y,modelNB.predict_proba(X)[:,1],pos_label=1) 
fpr1,tpr1,thresholds1 = roc_curve(Y,modelLR.predict_proba(X)[:,1],pos_label=1) 
axes[0].plot(fpr, tpr, color='r',label='贝叶斯ROC(AUC = %0.5f)' % auc(fpr,tpr)) 
axes[0].plot(fpr1, tpr1, color='blue',linestyle='-.',label='Logistic回归ROC(AUC = %0.5f)' % auc(fpr1,tpr1)) 
axes[0].plot([0, 1], [0, 1], color='navy', linewidth=2, linestyle='--')
axes[0].set_xlim([-0.01, 1.01])
axes[0].set_ylim([-0.01, 1.01])
axes[0].set_xlabel('FPR')
axes[0].set_ylabel('TPR')
axes[0].set_title('两个分类模型的ROC曲线')
axes[0].legend(loc="lower right")

pre, rec, thresholds = precision_recall_curve(Y,modelNB.predict_proba(X)[:,1],pos_label=1)
pre1, rec1, thresholds1 = precision_recall_curve(Y,modelLR.predict_proba(X)[:,1],pos_label=1)
axes[1].plot(rec, pre, color='r',label='贝叶斯总正确率 = %0.3f)' % accuracy_score(Y,modelNB.predict(X))) 
axes[1].plot(rec1, pre1, color='blue',linestyle='-.',label='Logistic回归总正确率 = %0.3f)' % accuracy_score(Y,modelLR.predict(X))) 
axes[1].plot([0,1],[1,pre.min()],color='navy', linewidth=2, linestyle='--')
axes[1].set_xlim([-0.01, 1.01])
axes[1].set_ylim([pre.min()-0.01, 1.01])
axes[1].set_xlabel('查全率R')
axes[1].set_ylabel('查准率P')
axes[1].set_title('两个分类模型的P-R曲线')
axes[1].legend(loc='lower left')
plt.show()

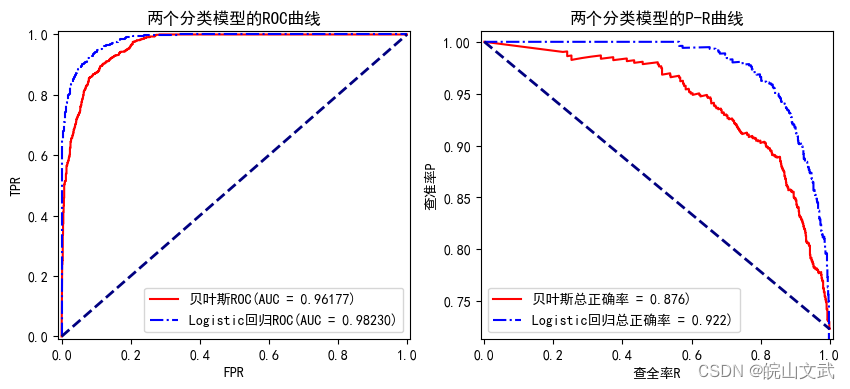
图中，两个回归模型的ROC曲线均远离基准线，且曲线下的面积分别约等于0.96和0.98，表明朴素贝叶斯模型虽然较好地实现二分类预测，但整体性能略低于Logistic回归模型。在P-R曲线中，随着查全率R的增加，Logistic回归模型的查准率P并没有快速下降，优于朴素贝叶斯分类器，且正确率较高。故对于该问题Logistic回归模型表现更好。