机器学习——降维算法-奇异值分解(SVD)
在机器学习中,降维是一种常见的数据预处理技术,用于减少数据集中特征的数量,同时保留数据集的主要信息。奇异值分解(Singular Value Decomposition,简称SVD)是一种常用的降维技术之一,它能够有效地提取数据集的主要特征,从而实现降维处理。本文将介绍降维算法的概念、奇异值分解的原理和应用、截断奇异值分解、以及奇异值分解的优缺点,并通过Python实现一个简单的SVD算法示例,最后给出总结。
1. 降维算法
降维算法是一种通过减少数据集中特征的数量来简化数据表示的技术。通过降维,我们可以消除数据中的冗余信息,提高计算效率,同时可以帮助我们更好地理解数据的结构和特性。常见的降维方法包括主成分分析(PCA)、奇异值分解(SVD)、线性判别分析(LDA)等。
2. 奇异值分解
奇异值分解是一种线性代数技术,用于将一个矩阵分解为三个矩阵的乘积,即将一个矩阵 A A A分解为三个矩阵 U U U、 Σ Σ Σ和 V V V的乘积,表示为 A = U Σ V T A = UΣV^T A=UΣVT。其中, U U U和 V V V是正交矩阵, Σ Σ Σ是对角矩阵,对角线上的元素称为奇异值。奇异值分解可以用于降维、数据压缩、以及矩阵逆的计算等领域。
3. 截断奇异值分解
截断奇异值分解是奇异值分解的一种变体,通过保留矩阵 A A A中的前 k k k个最大的奇异值,将矩阵 A A A近似地分解为 U k Σ k V k T UkΣkV^T_k UkΣkVkT,其中 U k U_k Uk、 Σ k Σ_k Σk和 V k V_k Vk是截断后的矩阵。截断奇异值分解可以实现数据的降维,同时保留数据集中的主要信息。
4. 奇异值分解的优缺点
优点:
- 能够提取数据集的主要特征,实现数据的降维处理。
- 对于大规模稀疏矩阵,也能够有效地进行分解。
缺点:
- 计算复杂度较高,对大规模数据集计算量较大。
- 无法处理非线性关系的数据。
Python实现算法
以下是使用Python实现的简单奇异值分解(SVD)算法示例:
import numpy as np
# 定义一个矩阵
A = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# 奇异值分解
U, s, VT = np.linalg.svd(A)
# 重构原始矩阵
Sigma = np.diag(s)
A_reconstructed = np.dot(U, np.dot(Sigma, VT))
print("Original matrix:")
print(A)
print("\nReconstructed matrix:")
print(A_reconstructed)
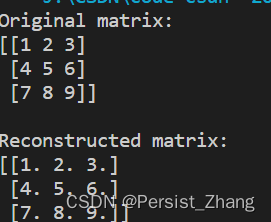
以上代码使用NumPy库中的linalg.svd函数实现了奇异值分解,并对原始矩阵进行了重构,最后输出了原始矩阵和重构矩阵。通过对比可以看出,重构矩阵与原始矩阵非常接近。
总结
本文介绍了奇异值分解(SVD)作为一种常用的降维算法,其原理、应用、以及优缺点。SVD能够提取数据集的主要特征,实现数据的降维处理,但也存在一些计算复杂度高的缺点。最后通过Python实现了一个简单的SVD算法示例,展示了奇异值分解的基本过程。在实际应用中,我们可以根据具体情况选择合适的降维方法来处理数据。