题目来源：https://leetcode.cn/problems/longest-common-subsequence/description/

C++题解（思路来源代码随想录）：动态规划。

        1. 确定dp数组（dp table）以及下标的含义

dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]。

        2. 确定递推公式

主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

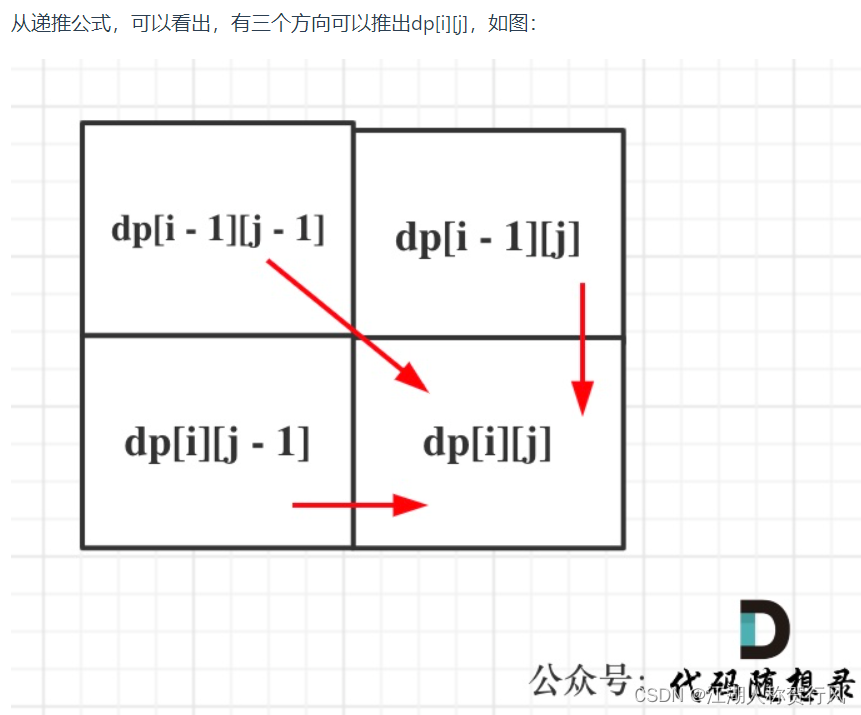
如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

代码：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n1 = text1.size(), n2 = text2.size();
        vector<vector<int>> dp(n1+1, vector<int>(n2+1, 0));
        for(int i = 0; i < n1; i++){
            for(int j = 0; j < n2; j++) {
                if(text1[i] == text2[j]) {
                    dp[i+1][j+1] = dp[i][j]+1;
                }
                else {
                    dp[i+1][j+1] = max(dp[i][j+1], dp[i+1][j]);
                }
            }
        }
        return dp[n1][n2];

    }
};