目录
- 一. KNN算法实现方式
- 1. 蛮力实现(brute)
- 2. KD树(kd_tree)
- 3. 球树(ball_tree)
- 二. KD Tree算法
- 1. 构建方式
- 2. KD Tree 查找最近邻
- 三. 球树(Ball Tree)
- 1. 构建方式
- 四. KNN评价
- 1. 优点
- 2. 缺点
- 五. 延申
- 1. KNN数据下采样策略
- 策略1
- 策略2
- 策略3
- 策略4 Condensed Nearest Neighbor()
KNN基础介绍篇中,我们通过KNN伪代码了解了该算法的逻辑;有没有发现,该算法在训练过程只是进行了数据加载,没有对数据进行任何其他的操作
对于样本数量较小的情况,或许该操作并无不妥;但是当面对海量的数据时,这种方式会有很明显的效率过低问题(即:输入待测样本后在所有数据中寻找K个最近的邻居,效率过低)
本篇,我们来解决这个问题
一. KNN算法实现方式
1. 蛮力实现(brute)
具体操作:
计算预测样本到所有训练集样本的距离
选择最小的k个距离即可得到K个最邻近点
缺点:
当特征数比较多、样本数比较多的时候,算法的执行效率比较低
2. KD树(kd_tree)
具体操作:
对训练数据进行建模,构建KD树
根据建好的模型来获取邻近样本数据
3. 球树(ball_tree)
具体操作:
球树是根据KD树修改后的一种算法,还有一些从KD树修改后的求解最邻近点的算法,例如:BBF Tree、MVP Tree等
二. KD Tree算法
KD Tree是KNN算法中用于计算最近邻的快速、便捷构建方式
- 当样本数据量较少时,我们可以使用brute的方法来求解最近邻,即计算到所有样本的距离
- 当样本数据量较大时,可以使用KD Tree来快速的计算,提高效率
1. 构建方式
假设样本集数据为 m ∗ n m*n m∗n的特征矩阵,即m个样本,n维数据
二叉搜索树
左子树的数值小于右子树
根节点一般为数据的中位数
节点判断:
分别计算n个特征的方差
用方差最大的第k个特征的中位数作为根节点
例子:
训练集数据
(
2
,
3
)
,
(
5
,
4
)
,
(
9
,
6
)
,
(
4
,
7
)
,
(
8
,
1
)
,
(
7
,
2
)
(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)
(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)
对于
x
(
1
)
x^{(1)}
x(1)轴的特征值,有:2,5,9,4,8,7;方差为5.81
对于
x
(
2
)
x^{(2)}
x(2)轴的特征值,有:3,4,6,7,1,2;方差为4.47
因此,数据按照
x
(
1
)
x^{(1)}
x(1)轴的特征进行划分,且以该轴中位数为根节点

KD树特征空间图:

对于左子树:
对于
x
(
1
)
x^{(1)}
x(1)轴的特征值,有:2,5,4;方差为1.56
对于
x
(
2
)
x^{(2)}
x(2)轴的特征值,有:3,4,7;方差为2.89
因此,数据按照
x
(
2
)
x^{(2)}
x(2)轴的特征进行划分,且以该轴中位数为根节点
对于右子树:
对于
x
(
1
)
x^{(1)}
x(1)轴的特征值,有:9,8;方差为0.25
对于
x
(
2
)
x^{(2)}
x(2)轴的特征值,有:1,6;方差为6.25
因此,数据按照
x
(
2
)
x^{(2)}
x(2)轴的特征进行划分,且以该轴中位数为根节点

KD树特征空间图:
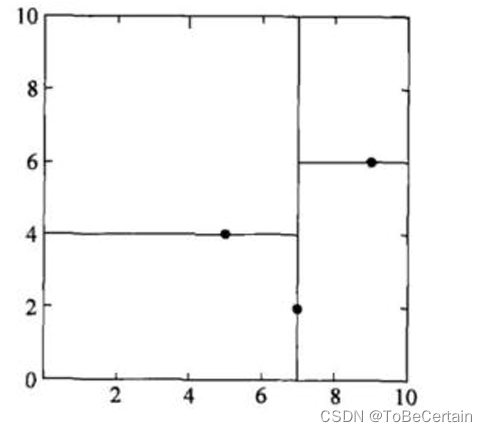
下面,我们对叶子节点进行划分(可以按照
x
(
1
)
x^{(1)}
x(1)轴划分),此时划分到每个叶子节点只有一个样本
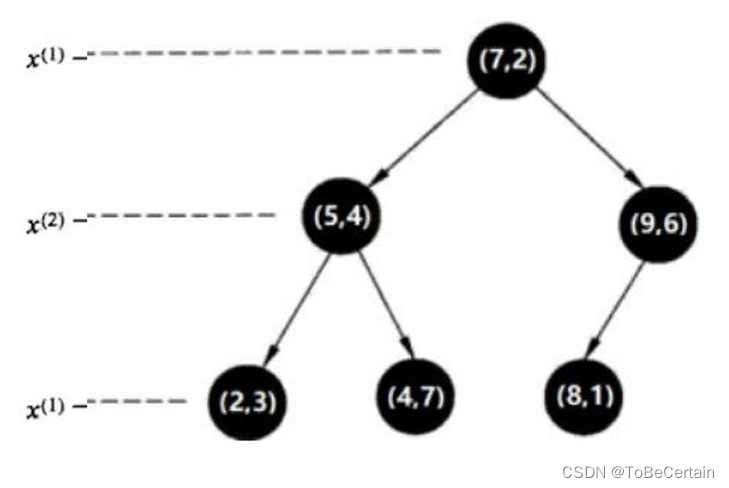
KD树特征空间图:
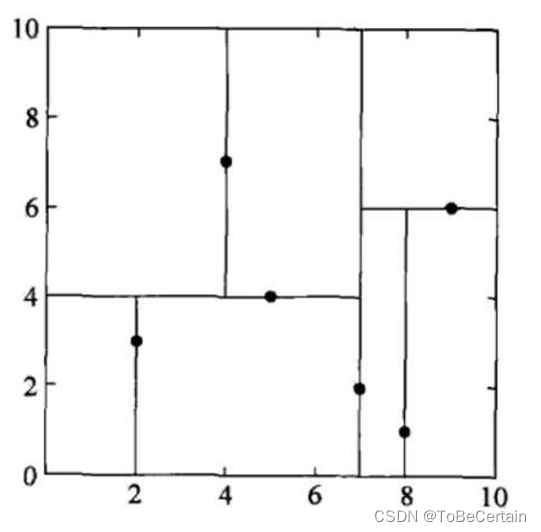
不加限制时,上述构造过程会划分到每个叶子节点只有一个样本;
但是没有必要这样做,可以限制样本数少于某个值时停止划分
每个节点都要保存是按哪个轴划分的
2. KD Tree 查找最近邻
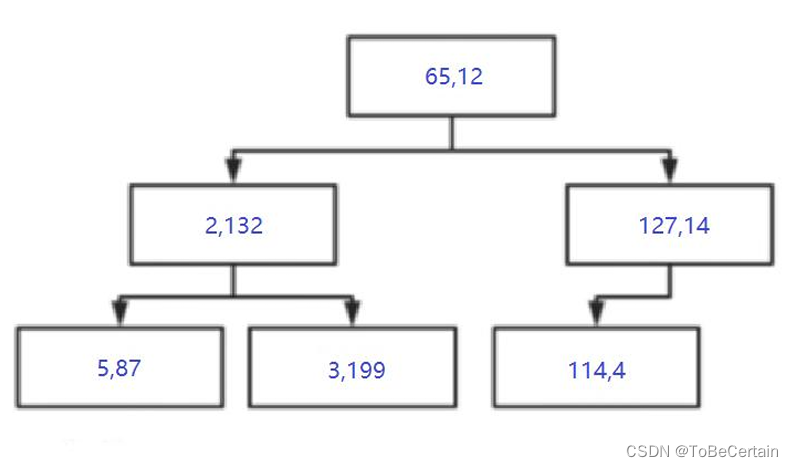
目标:求(25,135)的3个近邻,即K=3
-
操作1:初始化最近距离表
输入K值 初始化最近距离表 输出最近距离表 其中: 初始化的欧氏距离为inf,即+∞

-
操作2:回溯路径&计算距离
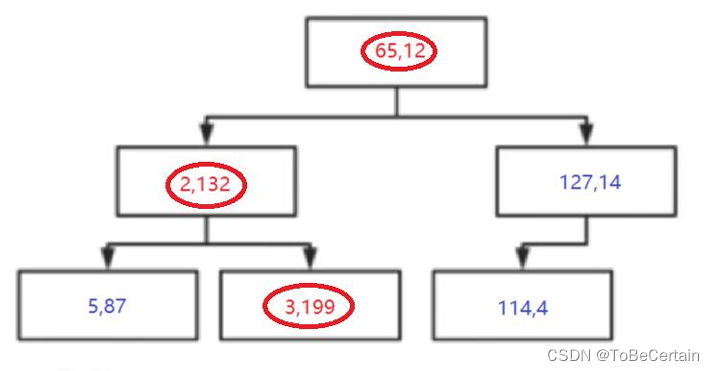
输入构建好的KD-Tree和待预测的样本点 输出回溯路径表 注意: 目标点可能在划分节点的左子树,也可能在划分节点的右子树 与目标点距离最近的点,不一定在目标点所在叶子节点上,有可能在其它节点上
节点 ( 65 , 12 ) (65,12) (65,12)的计算:
25-65 = 40
135-12 = 123
4 0 2 + 12 3 2 = 129.34 \sqrt{40^{2}+123^{2}}=129.34 402+1232=129.34 -
操作3:更新距离表

-
操作4:计算划分维度距离
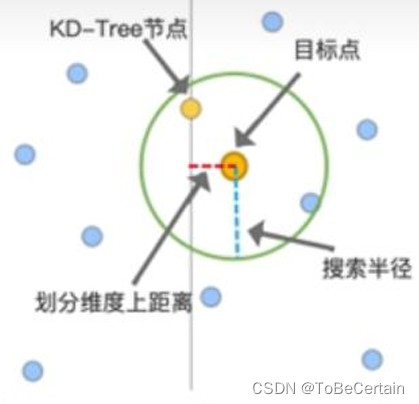
以129.34为搜索半径,划分维度距离
当搜索距离大于划分维度距离时,划分点另一侧的点也要纳入计算
如果 划分维度上目标点>划分点,则目标点在右子树,此时左子树也要纳入计算
如果 划分维度上目标点<划分点,则目标点在左子树,此时右子树也要纳入计算。
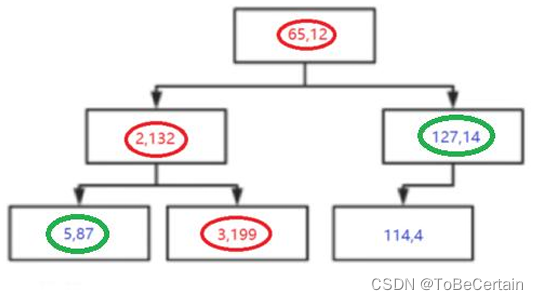
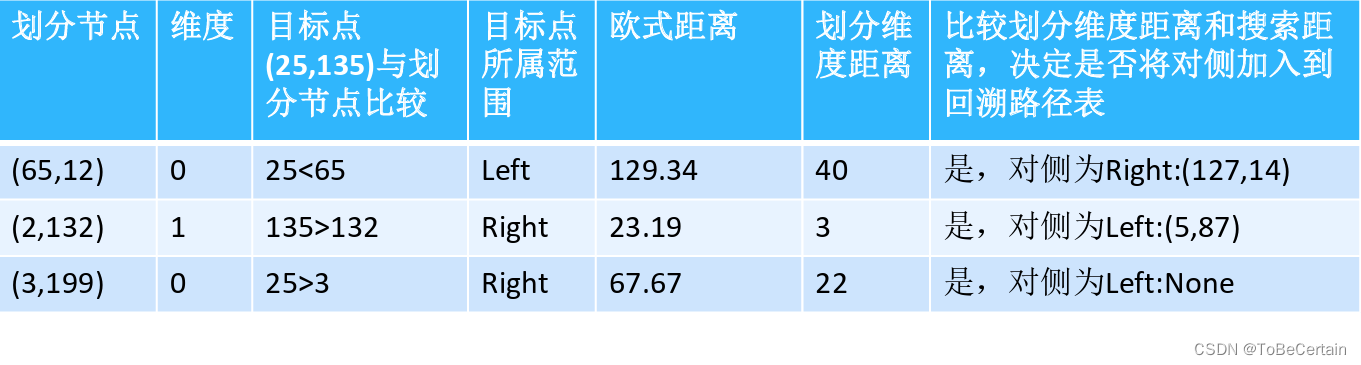
-
操作5:更新新回溯路径表&计算距离
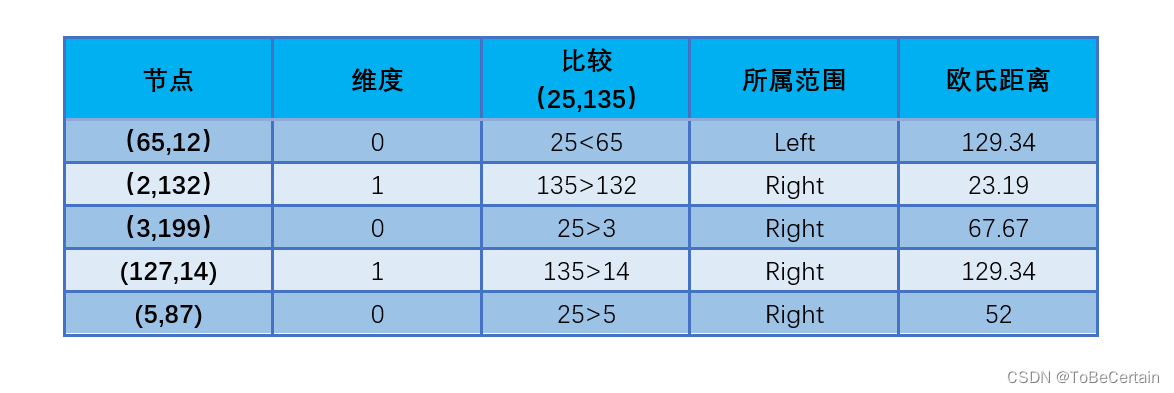
-
操作6:更新距离表
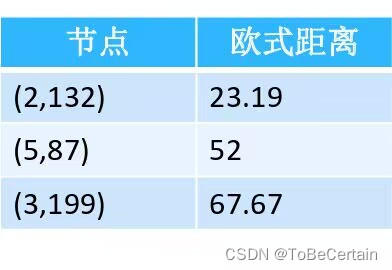
-
操作7:计算划分维度距离
以67.67为搜索半径,划分维度距离
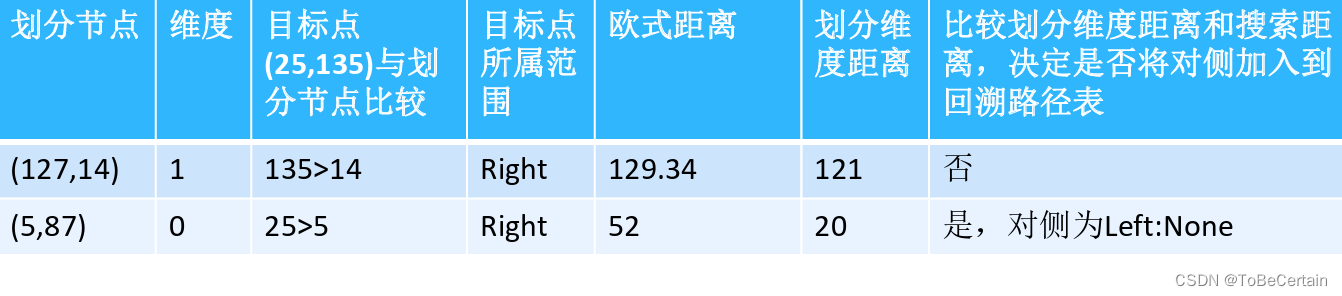
至此,没有产生新的回溯路径表,计算完成
最终,(25,135)的3个近邻为 ( 2 , 132 ) 、 ( 5 , 87 ) 、 ( 3 , 199 ) (2,132)、(5,87)、(3,199) (2,132)、(5,87)、(3,199)
三. 球树(Ball Tree)
对于KD树特征空间矩形图而言,在进行划分维度距离操作时,超球面时常会因菱角相交导致一些无关多余的搜索
针对KD树的上述缺陷,球树应运而生,通过将特征点转化为球状分割,从而减少无效相交
1. 构建方式
先构建一个超球体,这个超球体是可以包含所有样本的最小球体
具体操作:
从球中选择一个离球中心最远的点
选择第二个点离第一个点最远
将球中所有的点分配到这两个聚类中心附近
计算每个聚类的中心,以及聚类能够包含它所有数据点所需的最小半径
此时我们得到了两个子超球体(和KD树里面的左右子树对应)
对于这两个子超球体,递归执行步骤最终得到了一个球树
四. KNN评价
1. 优点
- 可以用来做分类(天然的多分类算法),也可以用来做回归;
- 可用于非线性分类
- 训练时间复杂度比支持向量机之类的算法低,仅为O(n)
- 和朴素贝叶斯之类的算法比,对数据没有假设,准确度高,对异常点不敏感
- 该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分
2. 缺点
- 计算量大,尤其是特征数非常多的时候
- 样本不平衡的时候,对稀有类别的预测准确率低
- KD树,球树之类的模型建立需要大量的内存
- 使用懒散学习方法,基本上不学习,导致预测时速度比起逻辑回归之类的算法慢
- 相比决策树模型,KNN模型可解释性不强
五. 延申
机器学习篇的分享即将接近尾声,这里我们对算法进一步阐述:
首先,某个算法可在整个数据集上进行训练,从而得到一个符合目标的模型;
当然,某个算法也可以作为大算法的一部分独立使用,以实现目标
比如:用线性回归在某几条数据上寻找一条目标直线
那么,对于KNN来说,该算法可以:
-
填缺失值
-
平衡数据
搜集更多的数据,使数据达到平衡 改变样本的数量(包括增加-上采样和减少-下采样) 数据增强(从现有的训练样本中生成新的高质量的训练样本) 改变样本重要度(就是给予不同的权重) 改变评价指标,使之更符合不平衡数据的评定 改变代价敏感函数(比如Cost-Sensitive算法) ... 前4个从样本层面解决数据不平衡问题 其余从算法层面解决数据不平衡问题
概念:
当数据不均衡的时,数据下采样,就是减少样本数量多的那种类型的样本数量
即:剔除掉训练集中的冗余样本,使模型做到较高的可用性
当数据不均衡的时,数据上采样,就是增加样本数量少的那种类型的样本数量
1. KNN数据下采样策略
策略1
- 计算每个多数类点到它的K个最近邻的少数类点的平均距离
- 比较所有多数类点到它的K个最近邻的少数类点的平均距离,选出平均距离最小的多数类点,删除
- 重复以上步骤,直至删除了足够多的多数类点
该策略的本质:
这些被删除的多数类点很可能距离少数类点较近或者处于分割的边界,区分力度较弱,可以删除
策略2
- 找到每个少数类点的K个最近邻(包括少数类点和多数类点),所有K近邻全部被保留
- 对于剩下的多数类点,计算每个点到它的M个近邻的平均距离,删除平均距离最大的点
- 重复以上步骤,直至删除了足够多的多数类点。
该策略的本质:
尽可能剔除距离少数类样本较远的多数类样本,即删除离群样本
策略3
如果一对距离最近的点属于不同的类,则它们称为一个Tomek link。
对于一个Tomek link,可以:
- 移除其中的多数类点
- 将两个点全部移除
该策略的本质:
一个Tomek link的两个点有可能是噪声或者在边界附近
策略4 Condensed Nearest Neighbor()
对于训练集中的任意一个样本A,计算其最近的同类样本和最近的非同类样本的距离
如果A距离最近的 同类样本的距离 < 最近的非同类样本 的距离,则该样本应该被保留
否则应该被删除
这个策略可以进行调整,比如:
- 在 k 个最近邻样本中,超过80%的样本与 x 是不同类样本,即可剔除 x
- 确定一个半径为 r 的超球体,在这个球体内的所有样本中,超过80%的样本与 x 是不同类样本,即可剔除 x
注意:以上四种策略可能会导致过度削减数据集,因此在使用时需要谨慎考虑
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
本文相关代码存放位置
【KNN算法代码实现 + 皮马人数据集】
祝愉快🌟!