最短路算法

稠密图与稀疏图
n为点数,m为边数。m远小于n的平方为稀疏图,m接近n的平方为稠密图。
稀疏图用邻接表存,稠密图用邻接矩阵存
朴素版dijkstra时间复杂度为O(n^2),对于稠密图可以ac,但遇到稀疏图时会TLE。
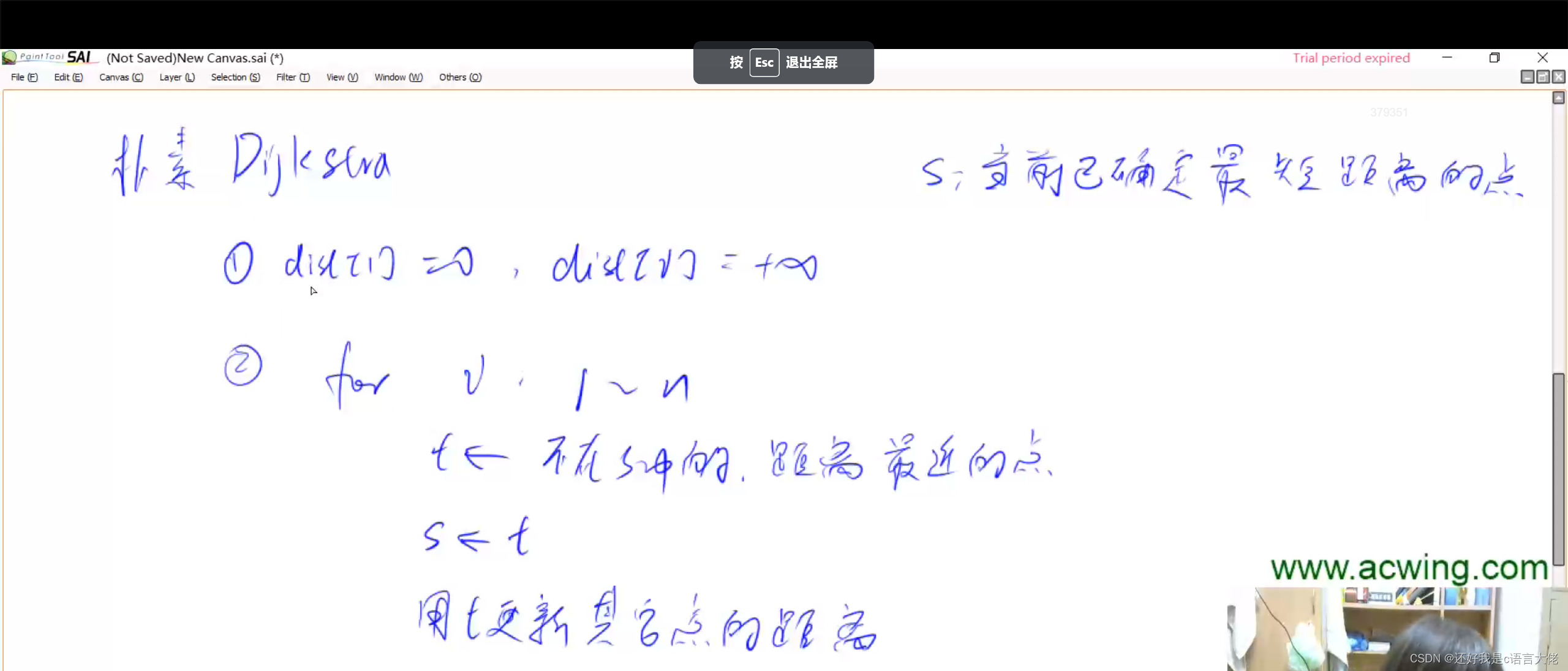
dijkstra函数实现步骤:
1、初始时,所有点都在圈内,所有点vis都=0,d[原点]=0,d[其他点]=+∞
2、从圈内选一个距离最小的点,打标记移除圈
3、对t的所有出边执行松弛操作(即尝试更新所有邻点的最小距离:dist[j] = min(dist[j],dist[t] + g[t][j]);)
4、重复第2、3步操作,知道圈内为空
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510;
int n,m;
int g[N][N]; //读入图,g[x][y] = s表示,该点为x,出边指向的点为y,边权为s
int dist[N]; //从一号点走到当前点的最短距离是多少
bool vis[N]; //当前点的最短距离是不是已经被确定了,确定了打上标记出圈
int dijkstra(){
memset(dist,0x3f,sizeof dist);
dist[1] = 0;
for(int i = 0;i < n - 1;i ++ ){
int t = -1;
/* 这个for循环就是找出距离原点最近的点,for循环遍历所有点,
if判断该点要没走过且该点到原点的距离小于t点到原点的距离,
将j赋值给t,这样就可以以此找到当前没有被打上标记且距离
原点最近的点了 */
for(int j = 1;j <= n;j ++ )
if(!vis[j] && (t == -1 || dist[t] > dist[j]))
t = j;
vis[t] = true; //t点距原点的最短距离已被确定,打上标记出圈
/* 现在找到t了,遍历一遍所有点,有一下几种情况
1.j点和t点之间无连接,那么g[t][j]=0x3f3f3f3f,特别大,会被pass
2.dist[j]<=dist[t]+g[t][j],源点到j点的距离,如果经过t后距离更长了,那么不考虑
3.dist[j]<=dist[t]+g[t][j],源点到j点的距离,经过t点距离更短了,那么修改dist[j]的值 */
for(int j = 1;j <= n;j ++ ){
dist[j] = min(dist[j],dist[t] + g[t][j]);
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
int main(){
cin >> n >> m;
memset(g,0x3f,sizeof g);
while(m -- ){
int x,y,z;
cin >> x >> y >> z;
g[x][y] = min(g[x][y],z);
}
cout << dijkstra() << endl;
return 0;
}堆优化版dijkstra 时间复杂度O(mlogn)
dijkstra函数实现步骤:
1、初始化,{0,1}入队,d[1] = 0,d[其他点] = max
2、从队头弹出距离原点距离最小的点ver,若ver扩展过则跳过,否则打标记
3、对u的所有出边执行松弛操作,把{d[j],j}压入队列
4、重复2、3步操作,直到队列为空
#include<iostream>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
typedef pair<int,int> PII;
const int N = 150010;
int n,m;
int h[N],w[N],e[N],ne[N],idx;
int dist[N];
bool vis[N];
int add(int a,int b,int c){
e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx,idx ++ ;
}
int dijkstra(){
memset(dist,0x3f,sizeof dist);
dist[1] = 0;
priority_queue< PII,vector<PII>,greater<PII> > heap;
heap.push({0,1});
while(heap.size()){
auto t = heap.top();
heap.pop();
int distance = t.first,ver = t.second;
if(vis[ver]) continue;
vis[ver] = true;
for(int i = h[ver];i != -1;i = ne[i]){
int j = e[i];
if(dist[j] > dist[ver] + w[i]) {
dist[j] = dist[ver] + w[i];
heap.push({dist[j],j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main(){
cin >> n >> m;
memset(h,-1,sizeof h);
while(m -- ){
int x,y,z;
cin >> x >> y >> z;
add(x,y,z);
}
cout << dijkstra() << endl;
return 0;
}