文章目录
- 第几个幸运数字
- 题目描述
- 答案:1905
- 生成法
- C++代码
- 代码详细注释
- 代码思路解释
第几个幸运数字
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
到x星球旅行的游客都被发给一个整数,作为游客编号。
x星的国王有个怪癖,他只喜欢数字3,5和7。
国王规定,游客的编号如果只含有因子:3,5,7,就可以获得一份奖品。
我们来看前10个幸运数字是:
3 5 7 9 15 21 25 27 35 45
因而第11个幸运数字是:49
小明领到了一个幸运数字 59084709587505,他去领奖的时候,人家要求他准确地说出这是第几个幸运数字,否则领不到奖品。
请你帮小明计算一下,59084709587505是第几个幸运数字。
答案:1905
生成法
首先,我们需要明白题目,即幸运数字只能有3,5,7这三个数作为因子,其他数都不行
那么,我们就只需要生成只有3,5,7因子的数,例如:
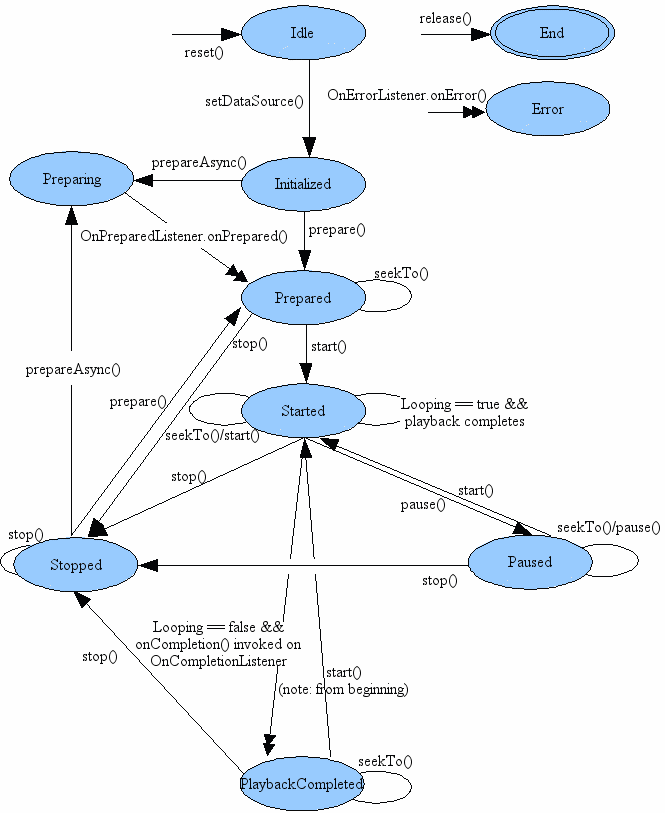
3*3,3*5,3*7,5*3,5*5,5*7,7*3,7*5,7*7,9*3,9*5,9*7……
如下图所示:

由图可得,如果我们要得到59084709587505这个数,我们需要对数组里存的数进行排序和去重,所以在代码中使用set容器,最后输出set存了多少数字即可
C++代码
这段代码的目的是找出一个给定的整数(在这个例子中是59084709587505)是第几个只包含3, 5, 7作为因子的“幸运数字”。下面是对代码的详细注释和解释。
代码详细注释
// 引入所有标准库
#include<bits/stdc++.h>
// 使用标准命名空间
using namespace std;
// 定义一个长整型别名ll
typedef long long ll;
// 定义幸运数字的上限为给定的数字
ll maxn=59084709587505;
// 定义一个集合p,用来存储幸运数字
set<ll> p;
int main()
{
// 定义一个数组a,包含数字3,5,7
int a[]={3,5,7};
// 定义一个变量tou,它将会是用来生成幸运数字的基数
ll tou=1;
// 无限循环
while(true)
{
// 遍历数组a
for(int i=0;i<3;i++)
{
// 将tou乘以3,5,7中的每个数
ll tt=tou*a[i];
// 如果计算出的数字小于或等于maxn,则将它加入到集合p中
if(tt<=maxn)
p.insert(tt);
}
// 找到集合p中大于tou的最小的数字,并更新tou
tou=*p.upper_bound(tou);
// 如果tou等于maxn,则终止循环
if(tou==maxn) break;
}
// 输出集合p的大小,即小明的幸运数字是第几个幸运数字
cout<<p.size();
return 0;
}
代码思路解释
代码的基本思路是生成一个幸运数字的集合,然后计算给定的幸运数字在集合中的位置。这里的幸运数字是指仅包含3、5、7作为因子的数字。这是通过以下步骤实现的:
-
初始化: 定义一个长整型的集合
p来存储生成的幸运数字,初始基数tou设置为1。 -
生成幸运数字: 通过一个无限循环,乘以3、5、7,并将结果小于等于给定数
maxn的数添加到集合p中。 -
更新基数: 使用
upper_bound函数来找到集合中大于当前基数tou的最小元素,并更新tou为这个元素。这一步确保了每次都在增加新的幸运数字到集合中。 -
终止条件: 当更新后的基数
tou等于maxn时,循环结束。 -
输出结果: 集合
p现在包含了小于等于maxn的所有幸运数字。输出集合的大小即得到给定的幸运数字是第几个。
最终,程序输出集合p的大小,这个大小就是小明幸运数字的排名。
重要的是要注意,这个程序假设给定的数字确实是一个幸运数字,因此它会出现在集合p中。程序利用了set在C++标准库中的性质,即它会自动排序且不包含重复元素。